[알고리즘/Java] 크루스칼(Kruskal) 알고리즘

✔ 목차

1. 크루스칼 알고리즘이란?
2. 크루스칼 알고리즘 과정
3. 크루스칼 알고리즘 구현 - Java

---

🔎 크루스칼 알고리즘이란?

최소 신장 트리 알고리즘
1. 크루스칼(Kruskal) 알고리즘
2. 프림(Prim) 알고리즘

크루스칼(Kruskal) 알고리즘

• 최소 신장 트리 알고리즘(MST)
• 간선을 하나씩 늘려감
• O(Elog V) 시간복잡도 가짐
• 탐욕법 사용
  
  

---

🔎 크루스칼 알고리즘 과정

초기 상태로 정점(=노드)는 서로 연결되어 있지 않다. 간선을 하나씩 추가하면서 MST를 만든다. 크루스칼 알고리즘을 수행하고 완성된 그래프는 최소 신장 트리이다. 간선을 추가하는 방식은 다음과 같다.

1) 크기가 가장 작은 간선부터 모든 간선을 살핀다. 이때 간선은 가중치에 대해 오름차순으로 정렬되어 있다.
2) 간선을 그래프에 포함 했을 때, MST에 사이클이 생기지 않으면 추가한다. 이 과정은 유니온 파인드 알고리즘을 이용한다.
정점 v와 정점 w를 잇는 간선e가 있을 때, 정점 v와 정점 w가 같은 부모 노드를 가진다면 간선 e는 MST에 추가하지 않는다.

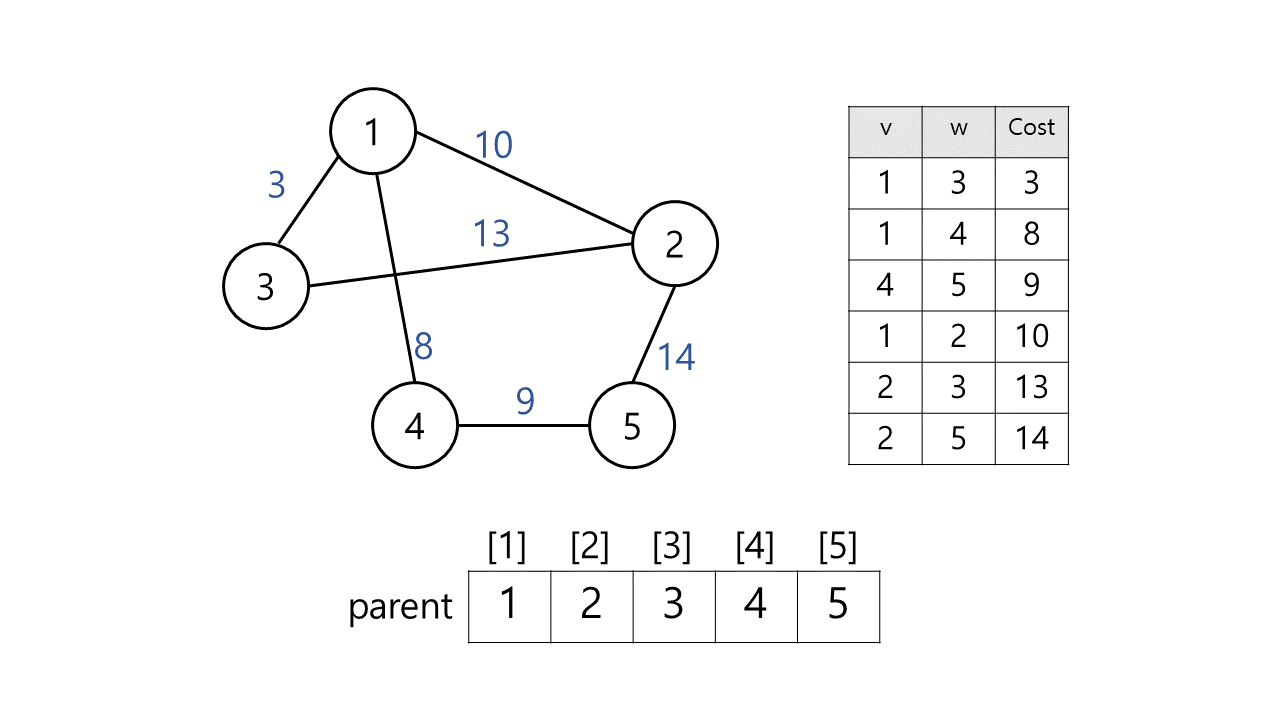
예시) 아래 그림과 같은 무방향 그래프가 있다. 초기 상태는 다음과 같다.

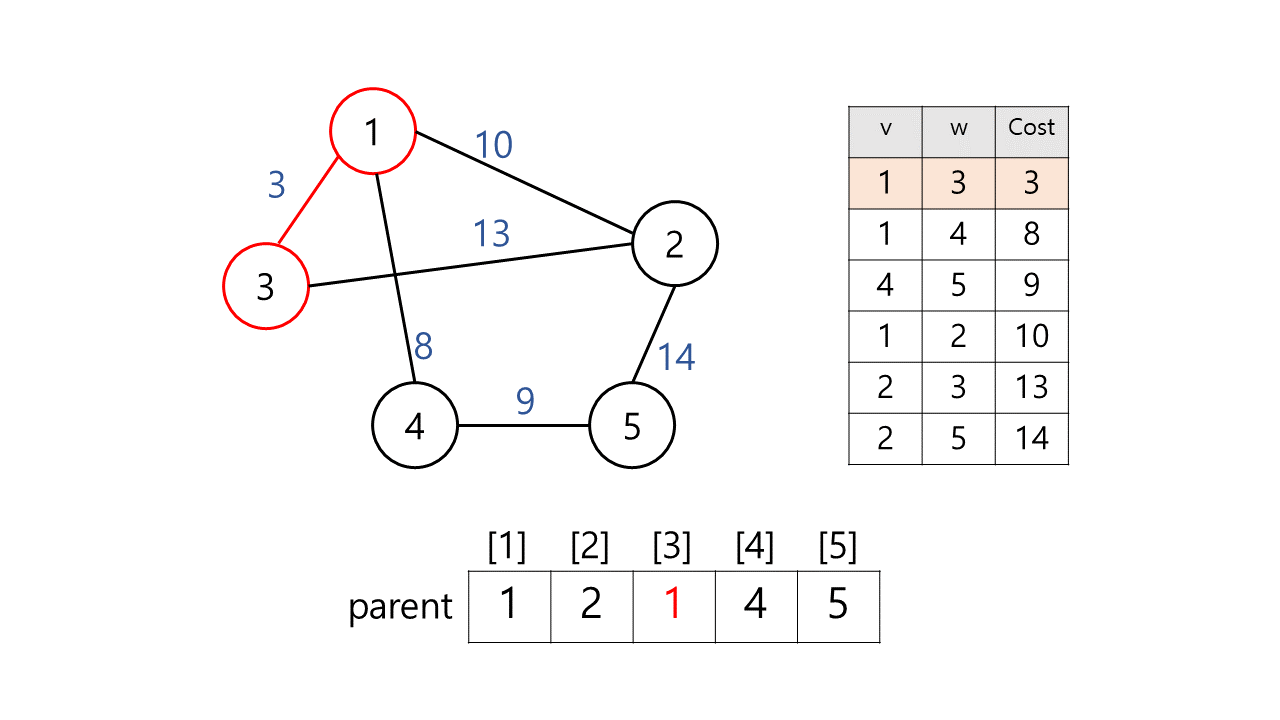
1) (v, w, cost) = (1, 3, 3)

• find(1) = 1, find(3) = 3
  부모 노드가 다르므로 이 간선을 MST에 추가했을 때 사이클이 생기지 않는다. 따라서 이 간선을 MST에 추가한다.
  정점 1과 정점 3을 union(1, 3)을 수행하여 같은 MST에 속해있도록 한다.
  

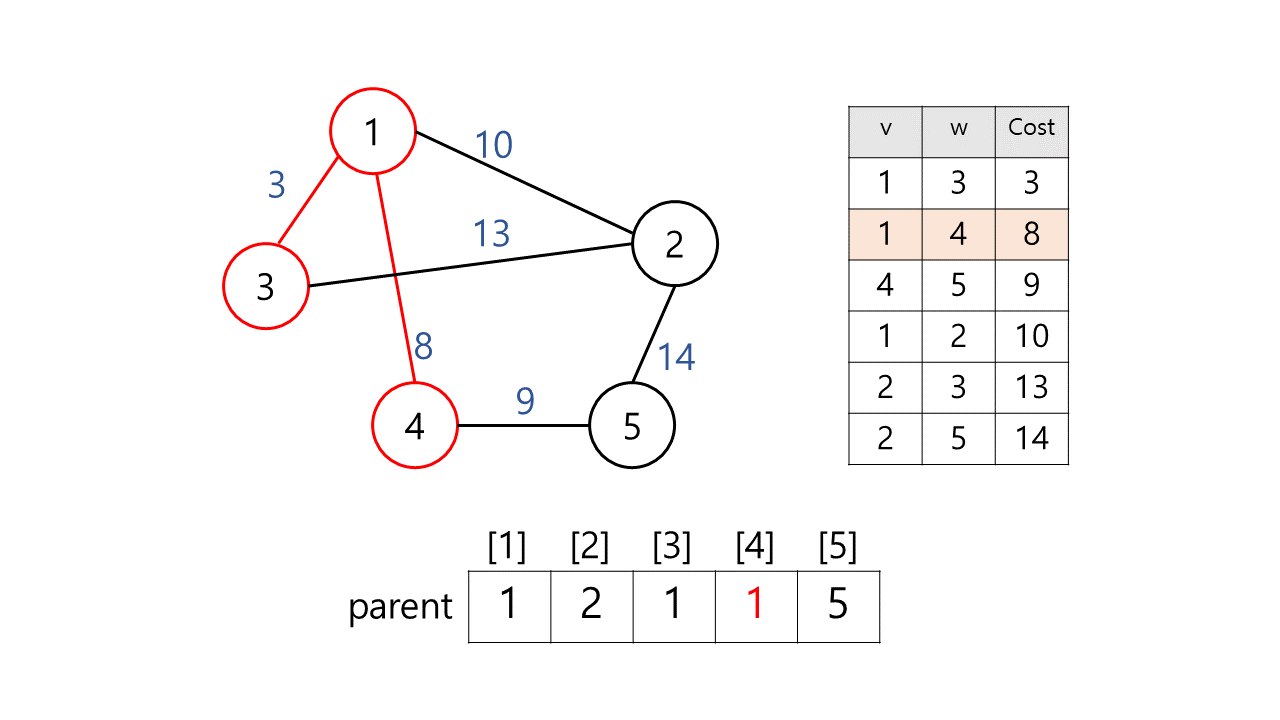
2) (1, 3, 3)

• find(1) = 1, find(4) = 4
  위와 동일한 이유로 간선을 추가한다.
  

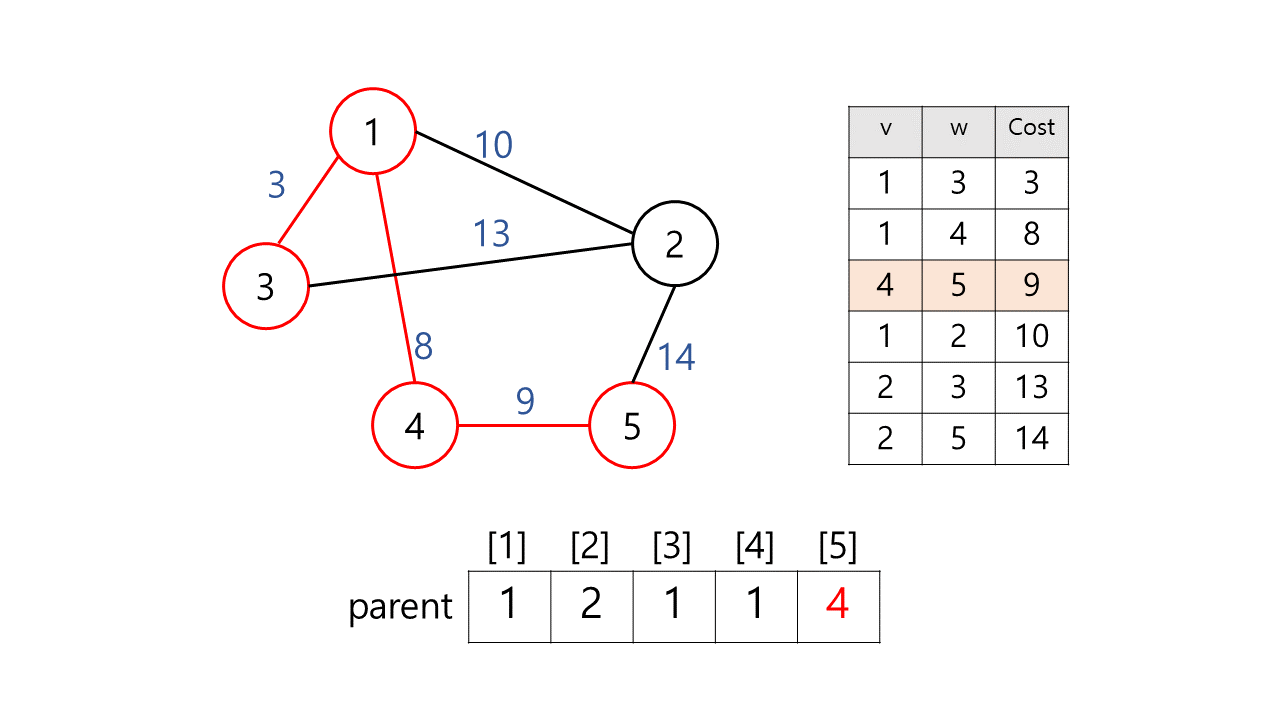
3) (4, 5, 9)

• find(4) = 1, find(5) = 5
  
  
  

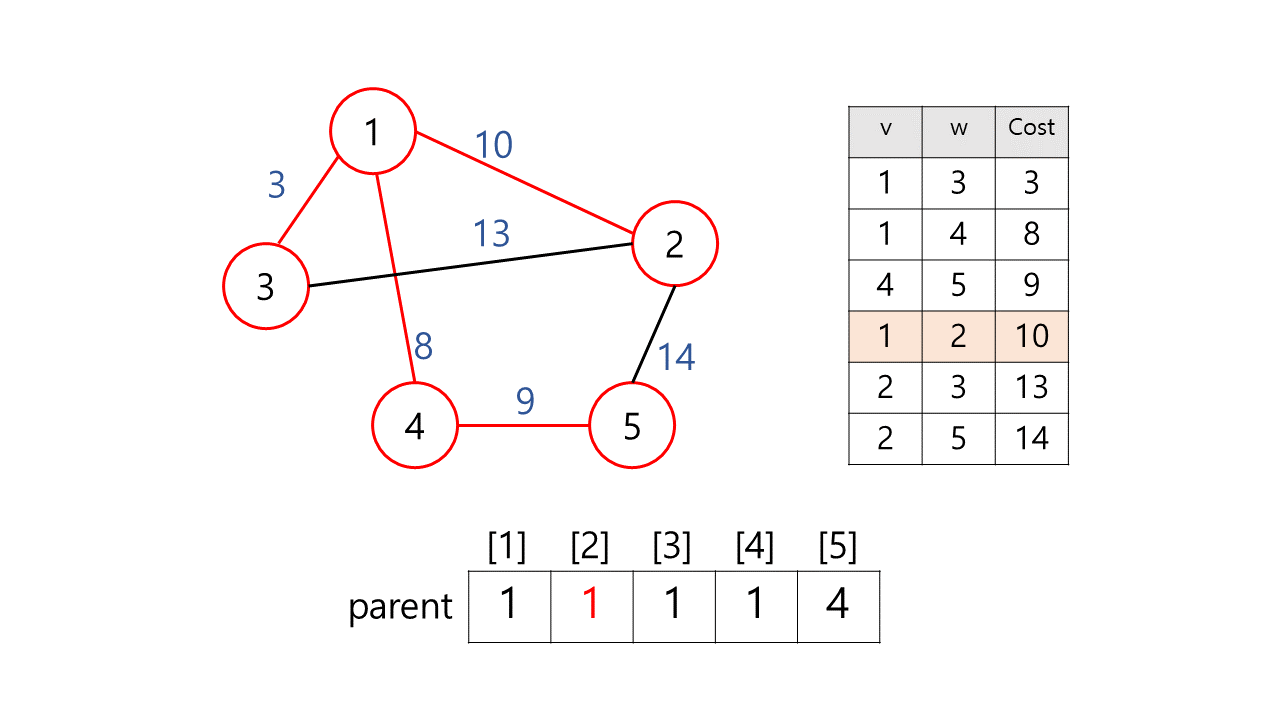
4) (1, 2, 10)

• find(1) = 1, find(2) = 2
  
  
  

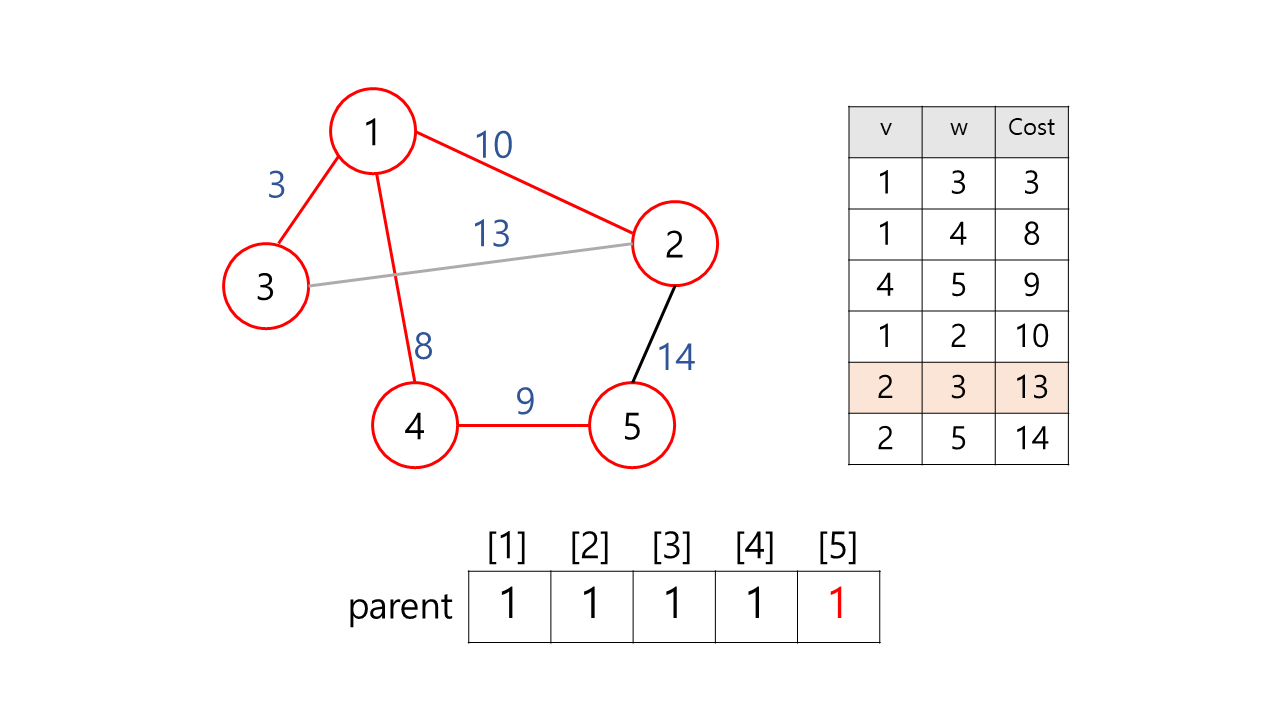
5) (2, 3, 13)

• find(2) = 1, find(3) = 1
  두 정점의 부모 노드가 같다. 이 간선을 MST에 추가할 경우 사이클이 생기므로 추가하지 않는다.
  
  
  

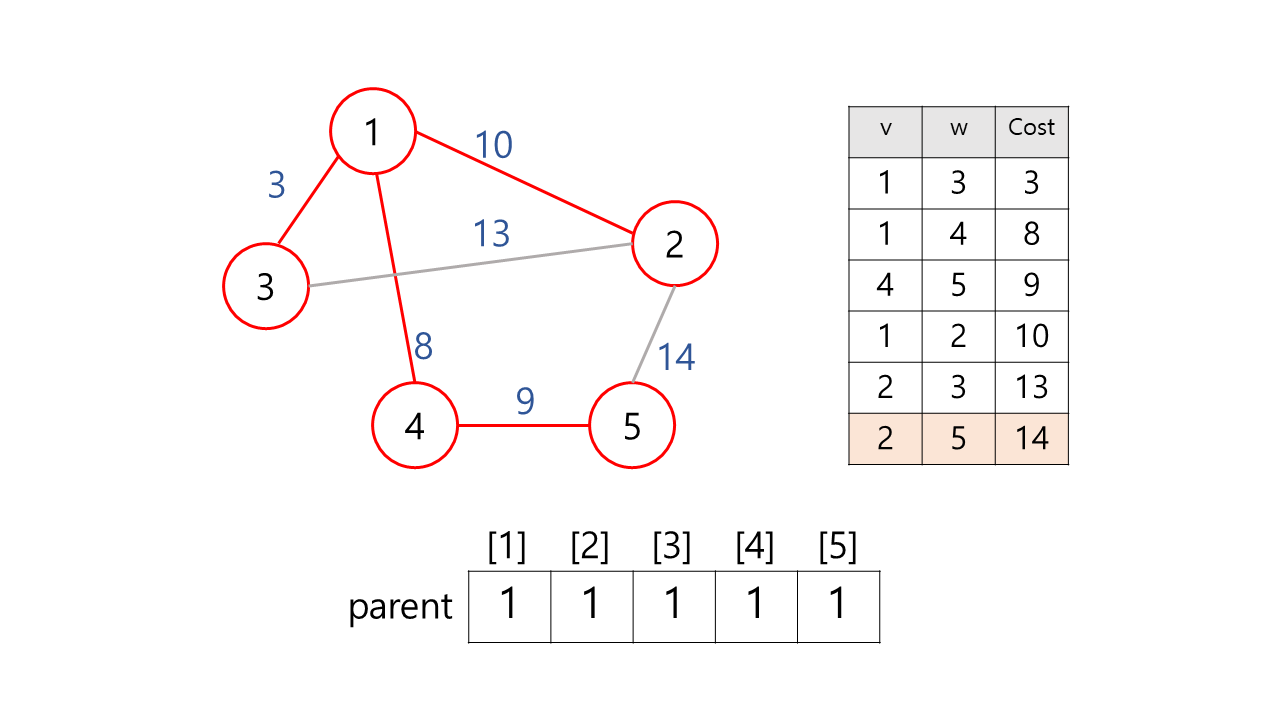
6) (2, 5, 14)

• find(2) = 1, find(5) = 1
  위와 동일한 이유로 추가하지 않는다.
  
  
  

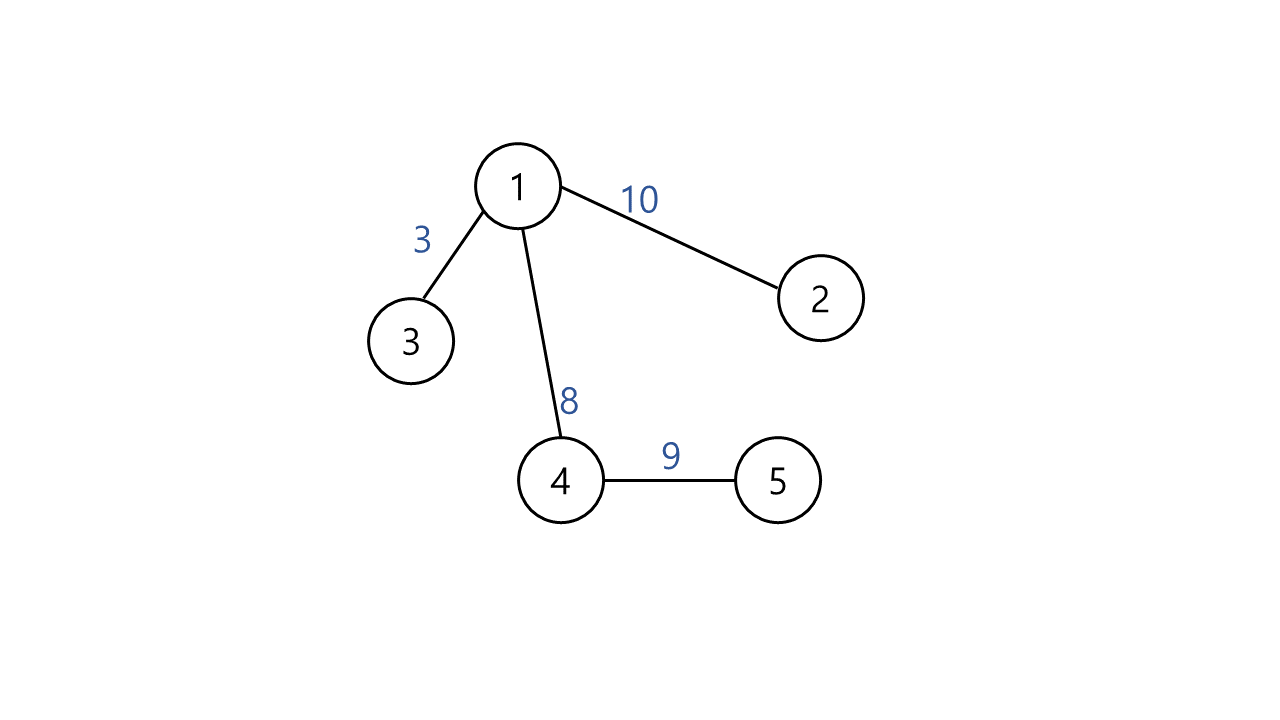
최종) 모든 간선을 살피고 남은 MST의 모습이다. 이 MST의 가중치의 총 합은 30이다.

---

💻 크루스칼 알고리즘 구현 - Java

2차원 배열 graph에 간선들을 저장했다. graph[i]는 i번째로 작은 간선이다.

크루스칼 알고리즘

public static void kruskal(int[][] graph, int[] parent) {
	int cost = 0;
	for(int i = 0; i < graph.length;i++) {
		if (find(parent, graph[i][0]) != find(parent, graph[i][1])) {
			cost += graph[i][2];
			union(parent, graph[i][0], graph[i][1]);
		}
	}
	System.out.println(cost);
}

전체 코드

public class Main {
	// 유니온 
	public static void union(int[] parent, int x, int y) {
		x = find(parent, x);
		y = find(parent, y);
		
		if(x < y) parent[y] = x;
		else parent[x] = y;
	}
    // 파인드
	public static int find(int[] parent, int x) {
		if(parent[x] == x) return x;
		else return find(parent, parent[x]);
	}
	
    // 크루스칼
	public static void kruskal(int[][] graph, int[] parent) {
		int cost = 0;
		for(int i = 0; i < graph.length;i++) {
			if (find(parent, graph[i][0]) != find(parent, graph[i][1])) {
				cost += graph[i][2];
				union(parent, graph[i][0], graph[i][1]);
			}
		}
        
        // 최소 신장 트리의 총 가중치 출력
		System.out.println(cost);
	}
	
	public static void main(String[] args) throws IOException {
    	// 간선 입력 받기, 그래프에 저장
		BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
		int n = Integer.parseInt(bf.readLine());
		int m = Integer.parseInt(bf.readLine());
		int[][] graph = new int[m][3];
		
		StringTokenizer st;
		for (int i = 0; i < m; i++) {
			st = new StringTokenizer(bf.readLine());
			graph[i][0] = Integer.parseInt(st.nextToken()); // 간선 나가는 정점
			graph[i][1] = Integer.parseInt(st.nextToken()); // 간선 들어오는 정점
			graph[i][2] = Integer.parseInt(st.nextToken()); // 가중치
		}
		
        // 간선 정렬
		Arrays.sort(graph, (o1, o2) -> o1[2] - o2[2]);
		
        // 부모노드 초기화
		int[] parent = new int[n + 1];
		for (int i = 0; i < parent.length; i++) {
			parent[i] = i;
		}
        
		//크루스칼 알고리즘 수행
		kruskal(graph, parent)
	}
}

입력
5
6
1 3 3
1 4 8
4 5 9
1 2 10
2 3 13
2 5 14

출력 결과
30