✔ 목차
- 프림 알고리즘이란?
- 프림 알고리즘 과정
- 프림 알고리즘 구현 - Java
🔎 프림 알고리즘이란?
최소 신장 트리 알고리즘
1. 크루스칼(Kruskal) 알고리즘
2. 프림(Prim) 알고리즘
프림(Prim) 알고리즘
- 최소 신장 트리 알고리즘(MST)
- 정점을 하나씩 늘려감
- 배열로 구현할 경우 시간 복잡도
o(n^2) - 최소 힙으로 구현할 경우 시간 복잡도
O(Elog n) - 탐욕법 사용
🔎 프림 알고리즘 과정
초기 상태로 정점(=노드)는 서로 연결되어 있지 않다. 정점과 연결된 간선을 하나씩 추가하면서 MST를 만든다.
프림 알고리즘은 시작 정점을 정해 우선 순위 큐에 넣는다. 우선 순위 큐에는 (정점, 가중치) 형식으로 저장되며, 첫 시작은 (시작 정점, 0)으로 넣는다.
우선 순위 큐가 빌 때까지 아래를 반복한다.
1) 우선 순위 큐에서 하나를 꺼낸다. 꺼낸 정점을 v라고 하겠다.
2) v가 이미 MST에 포함됐다면 1)로 돌아간다. 그렇지 않다면 아래를 진행한다.
3) v와 연결된 간선을 모두 살핀다. 간선 (w, cost)는 v와 정점 w 사이 연결된 간선이며 cost 가중치를 가진다. 만약 w를 방문하지 않았다면 우선순위 큐에 추가한다.
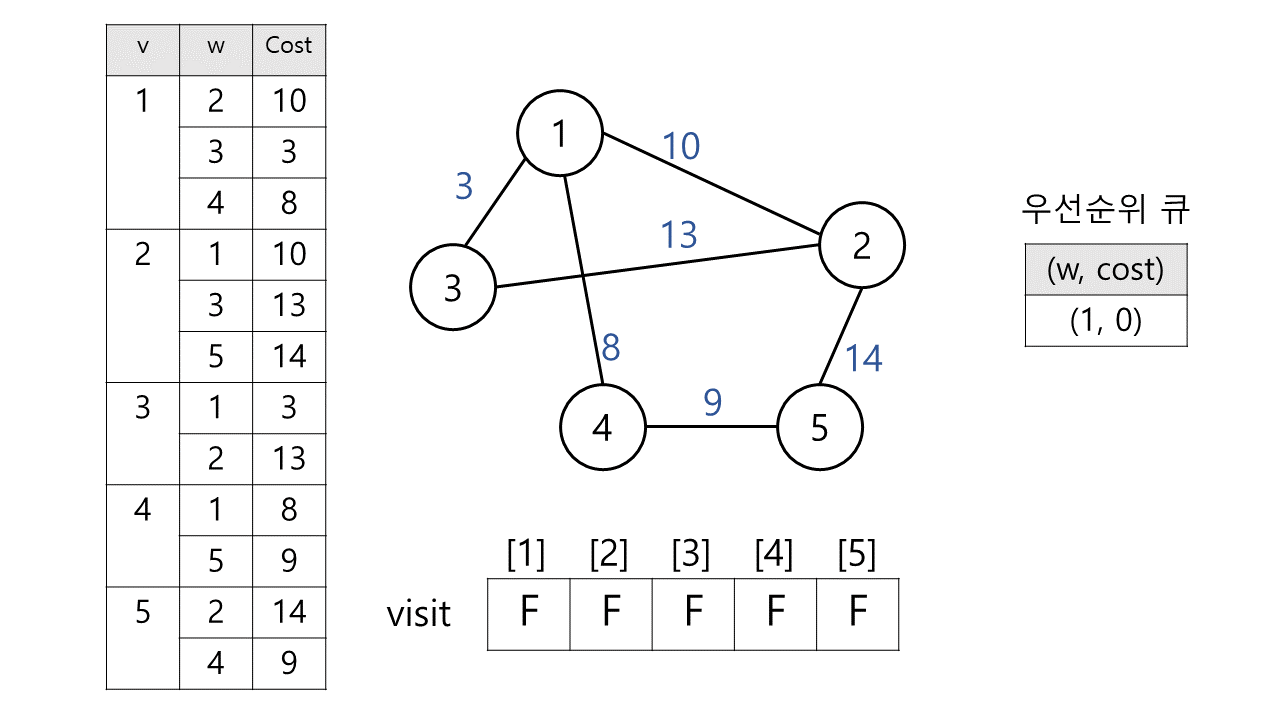
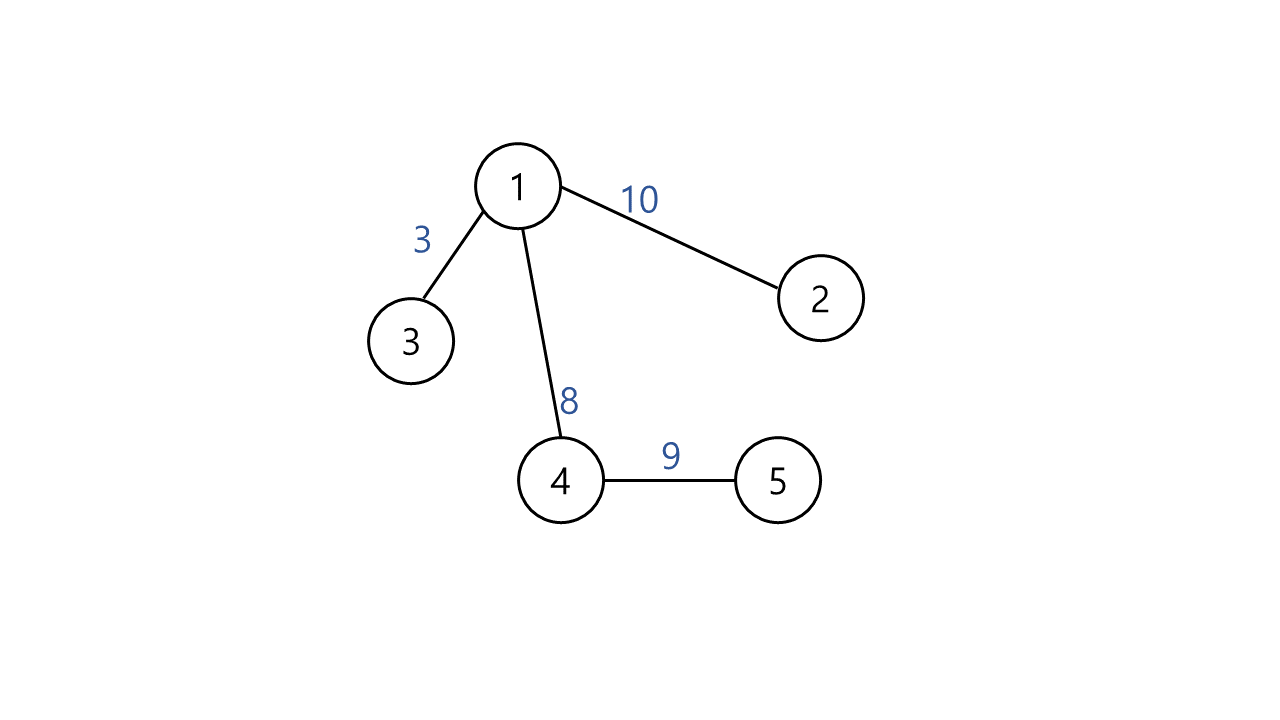
예시) 다음과 같은 그래프가 있다.
- 왼쪽 표 : 각 정점에 이어진 간선을 저장한 표이다.
visit:boolean배열로 각 정점을 방문했는지 체크한다.
정점을 방문 했다면 이미 MST에 포함된 정점이다.- 우선 순위 큐 : (
정점,가중치) 형태로 저장된다.
시작 정점은 1로 정했다. 따라서 우선 순위 큐에 (1, 0)를 저장했다.
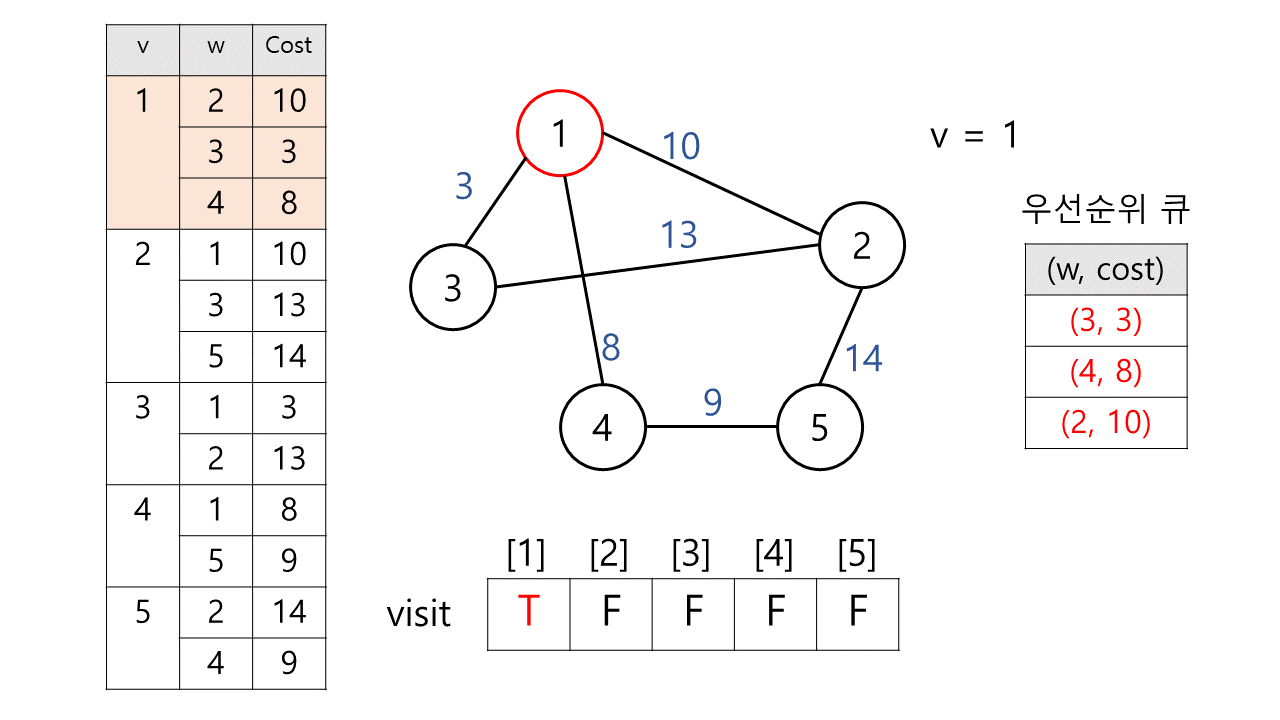
1) 우선 순위 큐에서 하나 꺼낸다. → (1, 0)
정점 1은 아직 방문하지 않았으므로 방문 체크를 한다. 이제 정점 1은 MST에 속해있다.
이후 정점 1과 연결된 간선을 모두 살핀다.
(3, 3)우선 순위 큐에 추가
정점 3은 아직 방문하지 않았다. 따라서 우선 순위 큐에 추가한다.(4, 8)우선 순위 큐에 추가(2, 10)우선 순위 큐에 추가
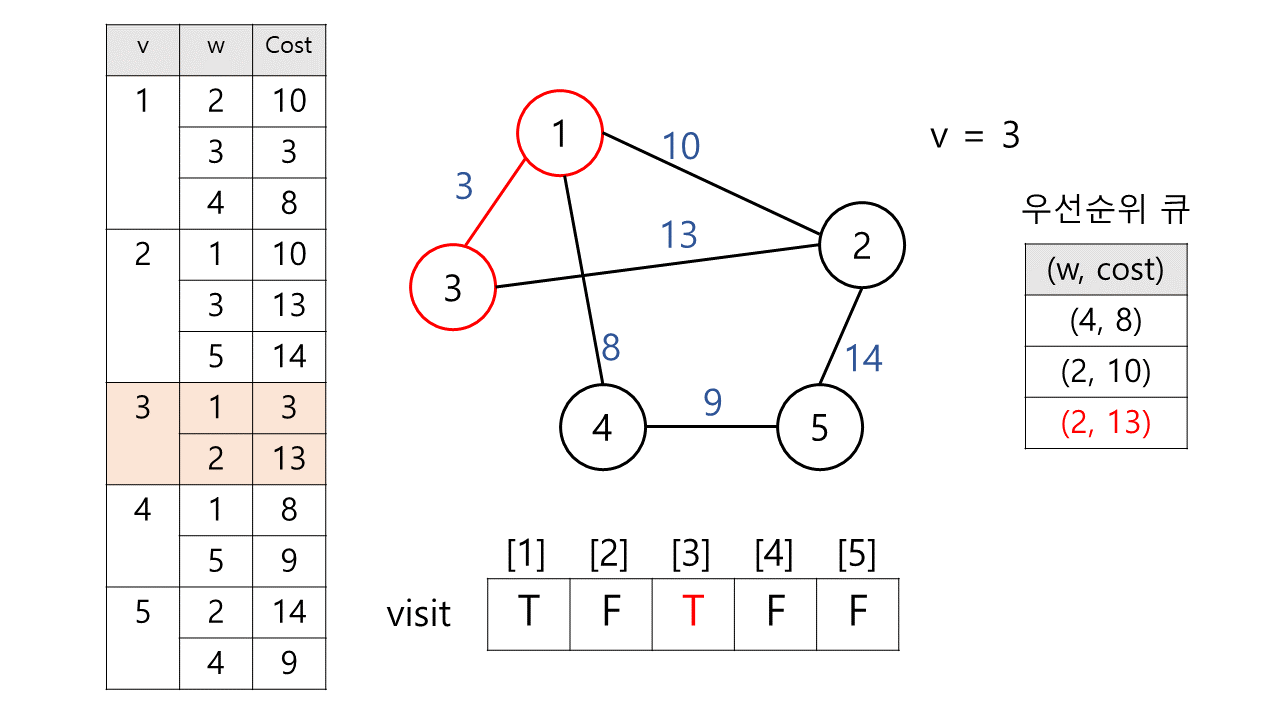
2) 우선 순위 큐에서 하나 꺼낸다. → (3, 3)
정점 3은 아직 방문하지 않았으므로 방문 체크를 한다. MST에 정점 3과 가중치 3이 추가된다.
이후 정점 3과 연결된 간선을 모두 살핀다.
(1, 3)우선 순위 큐에 추가 X
정점 1은 이미 방문했다. 즉, 이미 MST에 포함된 정점이므로 우선 순위 큐에 추가하지 않는다.(2, 13)우선 순위 큐에 추가
정점 2은 아직 방문하지 않았다. 따라서 우선 순위 큐에 추가한다.
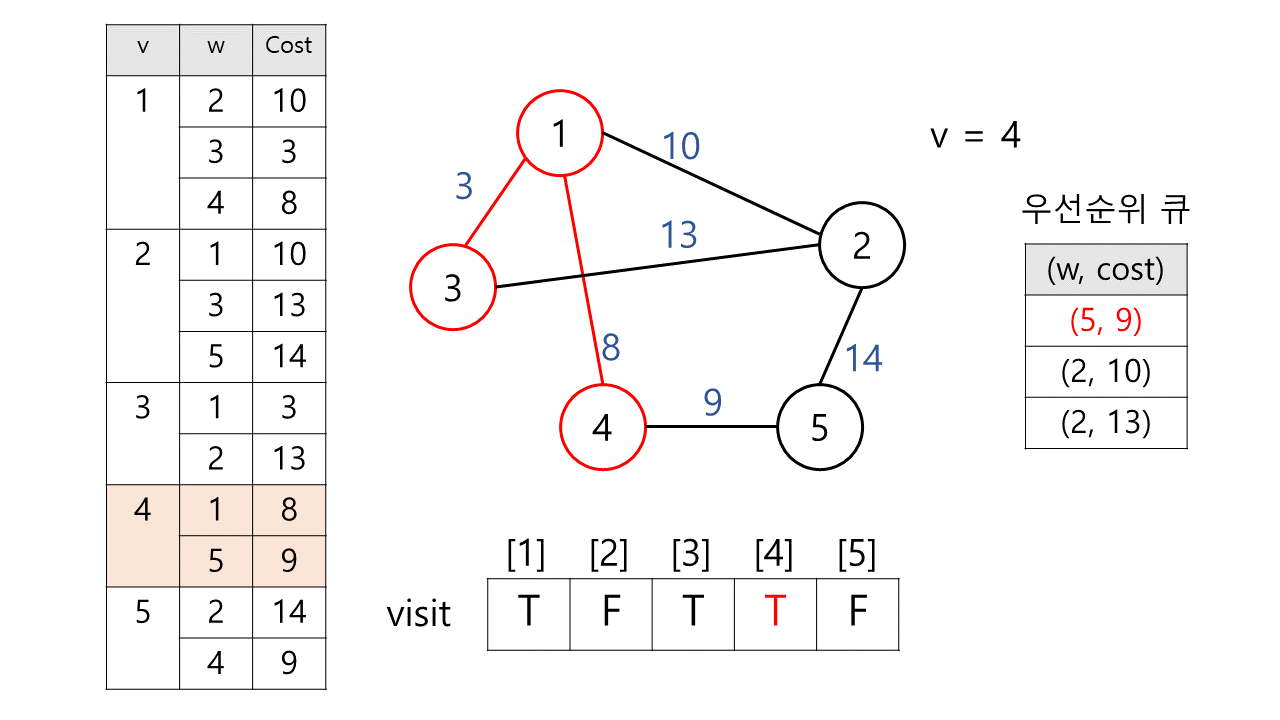
3) 우선 순위 큐에서 하나 꺼낸다. → (4, 8)
정점 4은 아직 방문하지 않았으므로 방문 체크를 한다. MST에 정점 4와 가중치 8이 추가된다.
이후 정점 4와 연결된 간선을 모두 살핀다
(1, 4)우선 순위 큐에 추가 X(5, 9)우선 순위 큐에 추가
4) 우선 순위 큐에서 하나 꺼낸다. → (8, 14)
정점 5는 아직 방문하지 않았으므로 방문 체크를 한다. MST에 정점 5와 가중치 9가 추가된다.
이후 정점 5와 연결된 간선을 모두 살핀다
(2, 14)우선 순위 큐에 추가(4, 9)우선 순위 큐에 추가 X
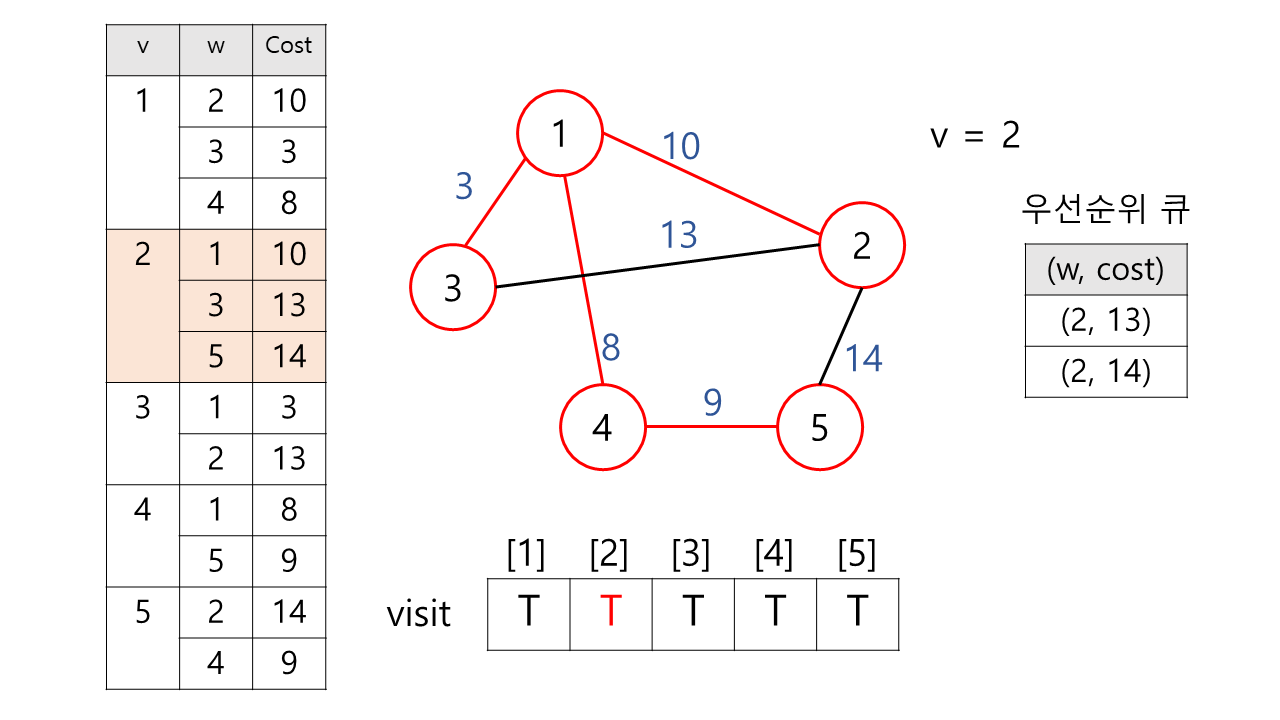
5) 우선 순위 큐에서 하나 꺼낸다. → (2, 10)
정점 2는 아직 방문하지 않았으므로 방문 체크를 한다. MST에 정점 2와 가중치 10이 추가된다.
이후 정점 2와 연결된 간선을 모두 살핀다
(1, 10)우선 순위 큐에 추가 X(3, 13)우선 순위 큐에 추가 X(5, 14)우선 순위 큐에 추가 X
연결된 간선 모두 이미 MST에 포함된 정점과 연결되어 있으므로 우선 순위 큐에 포함하지 않는다.
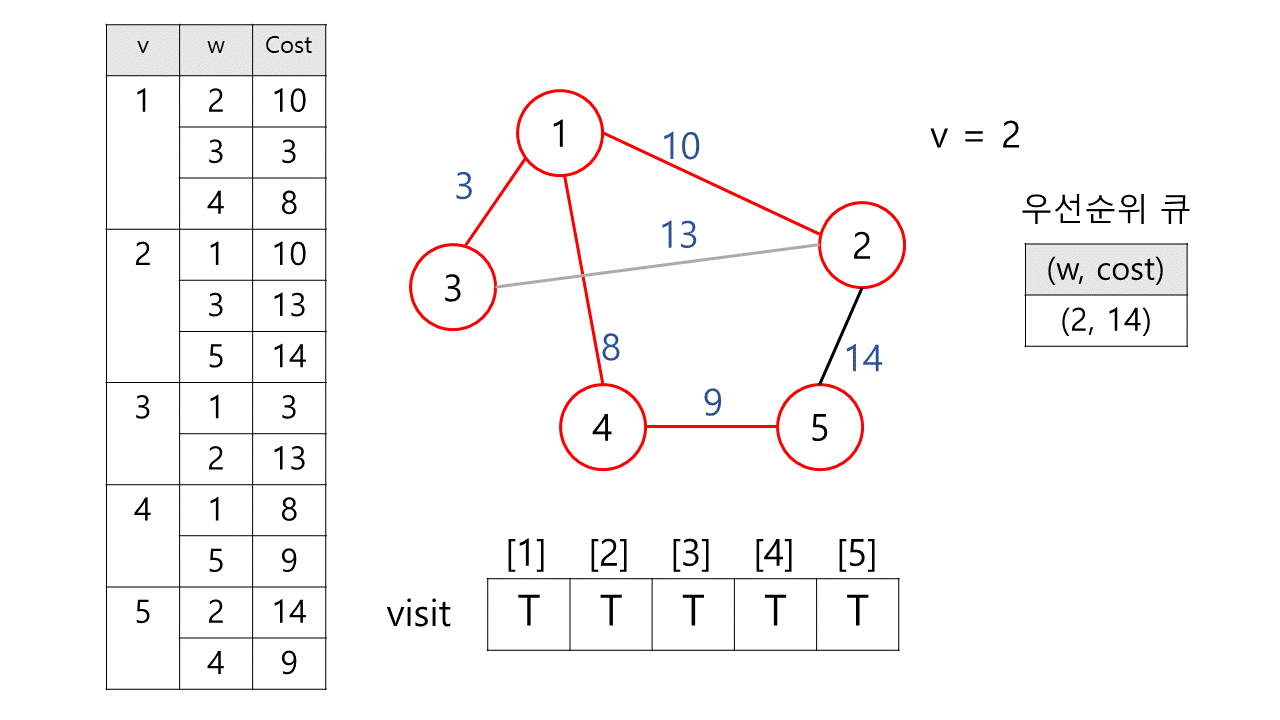
6) 우선 순위 큐에서 하나 꺼낸다. → (2, 13)
정점 2는 이미 방문했다. 즉, 이미 MST에 포함된 상태이므로 건너뛴다.
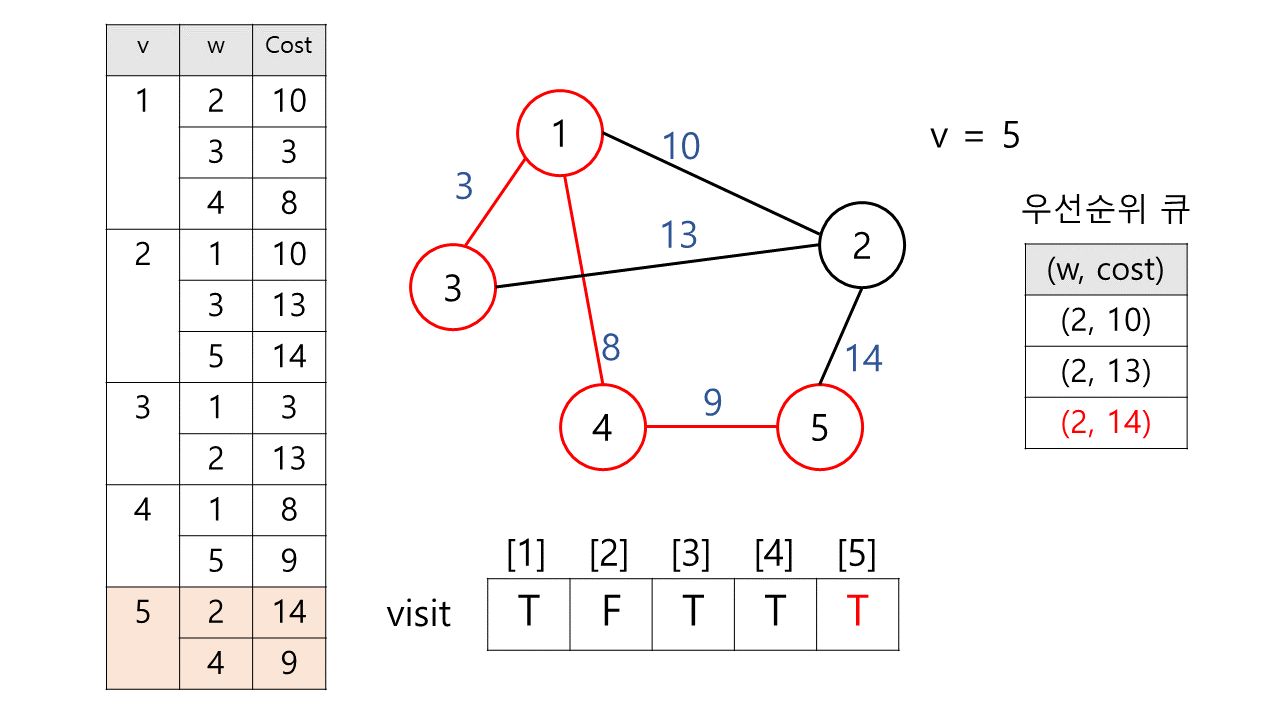
7) 우선 순위 큐에서 하나 꺼낸다. → (2, 14)
위와 동일한 이유로 건너뛴다.
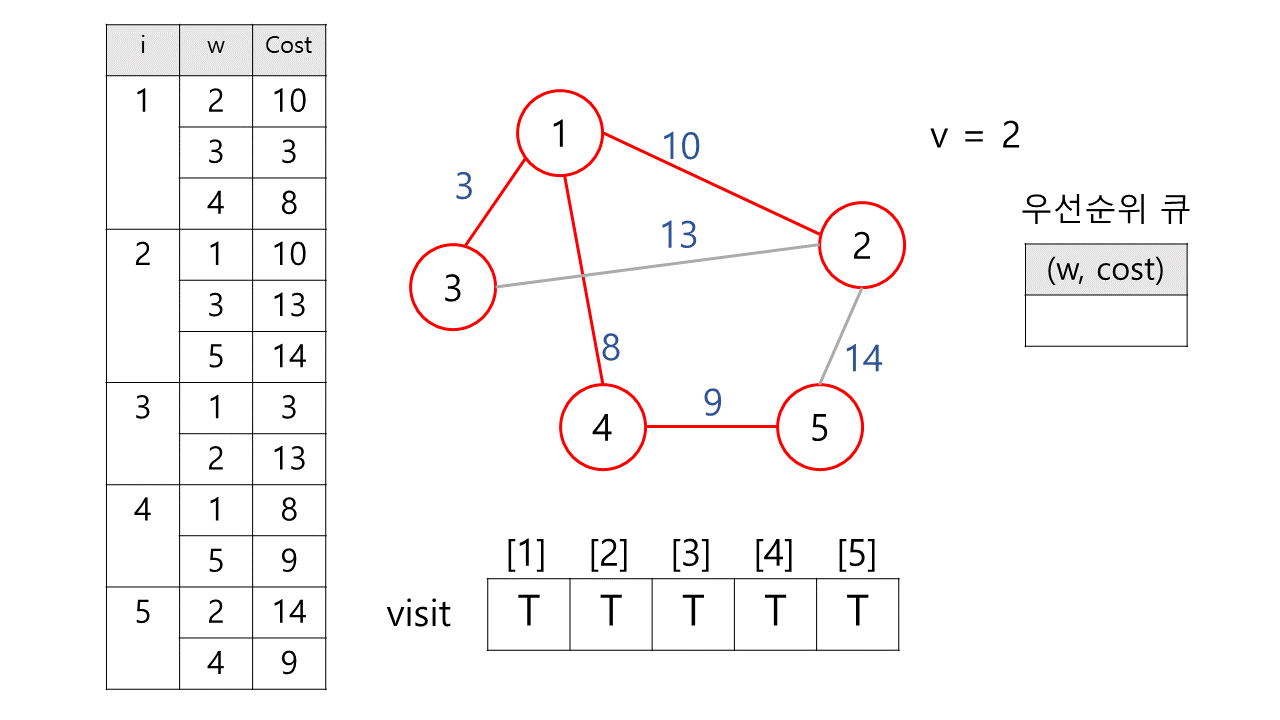
최종) 우선 순위 큐가 비었으므로 MST가 완성되었다. 아래는 최종 MST의 모습이며 총 가중치는 30이다.
💻 프림 알고리즘 구현 - Java
우선순위 큐를 이용해 구현했다. 그래프는 인접 리스트로 구현했다.
프림 알고리즘
// 간선 저장 위한 클래스
class Edge implements Comparable<Edge>{
int w; // 간선 들어오는 정점
int cost; // 간선 가중치
Edge(int w, int cost){
this.w = w;
this.cost = cost;
}
// 간선 오름차순으로 정렬
@Override
public int compareTo(Edge o) {
return this.cost - o.cost;
}
}
// 프림 알고리즘
public static void prim(int start, int n) {
boolean[] visit = new boolean[n + 1];
PriorityQueue<Edge> pq = new PriorityQueue<>();
pq.offer(new Edge(start, 0));
int total = 0;
while(!pq.isEmpty()) {
Edge edge = pq.poll();
int v = edge.w;
int cost = edge.cost;
//방문 했으면 건너뜀
if(visit[v]) continue;
visit[v] = true;
total += cost;
for(Edge e : graph[v]) {
if(!visit[e.w]) {
pq.add(e);
}
}
}
// 완성된 최소 신장 트리의 총 가중치 합 출력
System.out.println(total);
}전체 코드
class Edge implements Comparable<Edge>{
int w;
int cost;
Edge(int w, int cost){
this.w = w;
this.cost = cost;
}
@Override
public int compareTo(Edge o) {
return this.cost - o.cost;
}
}
public class prim_main {
static List<Edge>[] graph;
public static void prim(int start, int n) {
boolean[] visit = new boolean[n + 1];
PriorityQueue<Edge> pq = new PriorityQueue<>();
pq.offer(new Edge(start, 0));
int total = 0;
while(!pq.isEmpty()) {
Edge edge = pq.poll();
int v = edge.w;
int cost = edge.cost;
if(visit[v]) continue;
visit[v] = true;
total += cost;
for(Edge e : graph[v]) {
if(!visit[e.w]) {
pq.add(e);
}
}
}
System.out.println(total);
}
public static void main(String[] args) throws IOException {
// 그래프 입력, 저장
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(bf.readLine());
int m = Integer.parseInt(bf.readLine());
// 그래프 선언, 간선 리스트로 표현
graph = new ArrayList[n + 1];
for (int i = 0; i < graph.length; i++) graph[i] = new ArrayList<>();
StringTokenizer st;
for (int i = 0; i < m; i++) {
st = new StringTokenizer(bf.readLine());
int v = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
graph[v].add(new Edge(w, cost));
graph[v].add(new Edge(v, cost));
}
// 프림 알고리즘 수행
prim(1, n);
}
}
입력
5
6
1 3 3
1 4 8
4 5 9
1 2 10
2 3 13
2 5 14
출력 결과
30


//프림 알고리즘 수행
-> 이 주석 윗줄에 graph에 추가하는 부분에 오타있는 것 같아요
밑에꺼는 graph[w].add여야 할 것 같은데 graph[v].add라고 되어있네요