✔ 목차
- 최소 신장 트리란?
- 최소 신장 트리 알고리즘
🔎 최소 신장 트리란?
신장 트리(Spanning Tree)
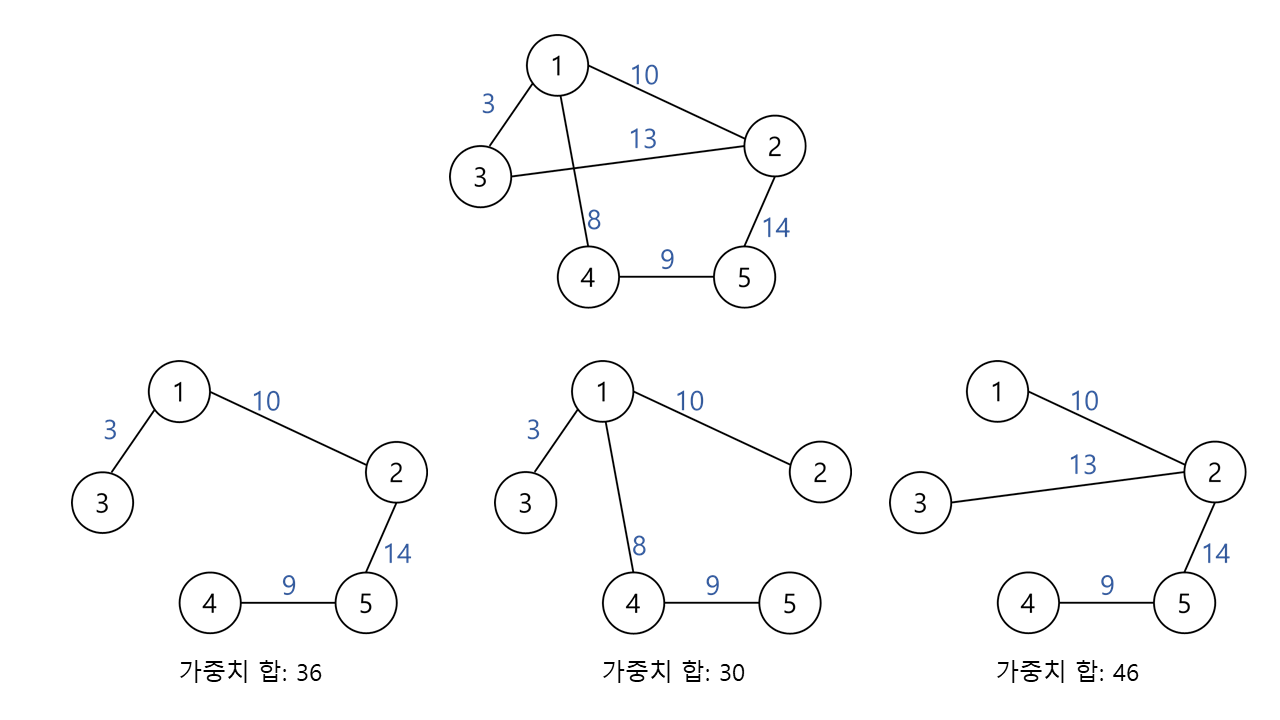
- 위의 그림 그래프에서 아래 그래프 3개 모두 신장 트리(3개 말고 더 있을 수 있음)
- 그래프의 모든 정점을 포함하는 트리
- 그래프의 최소 연결 부분 그래프로 사이클이 없음
- 정점의 개수
n개면 간선의 개수n-1개 가짐 - 하나의 그래프에 많은 신장 트리 존재
최소 신장 트리(MST, Minimum Spanning Tree)
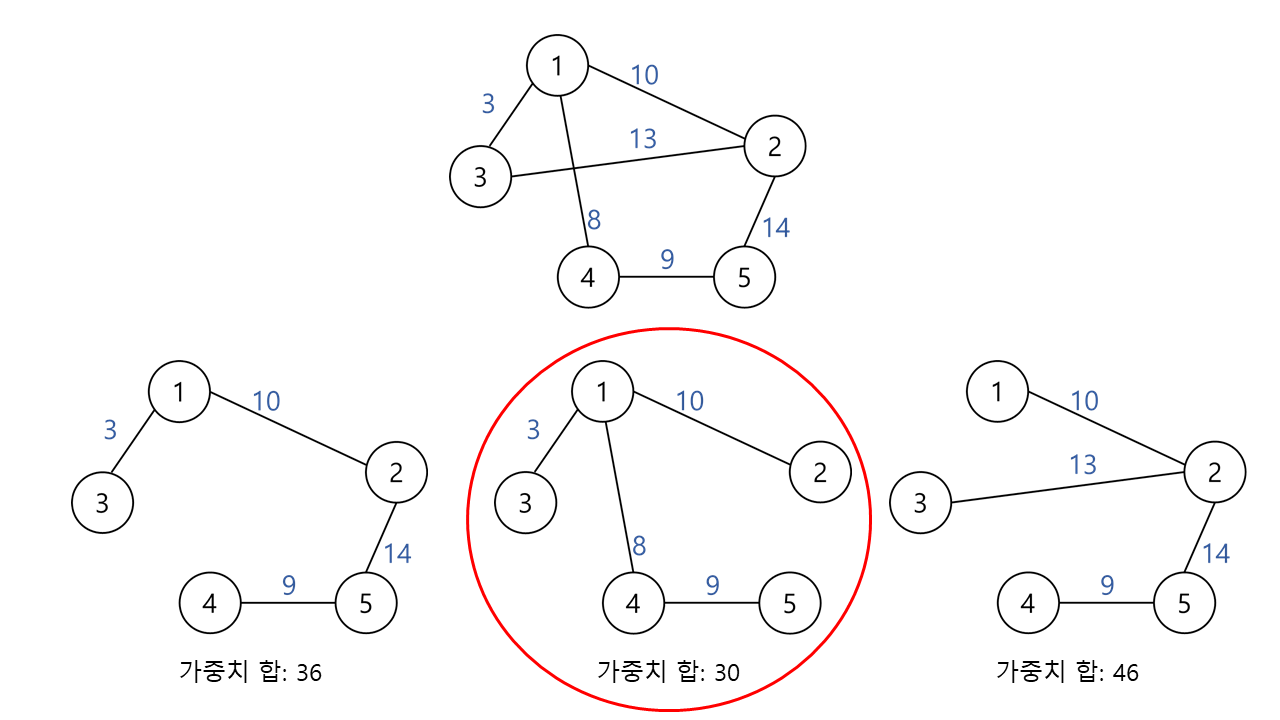
- 가운데 신장 트리는 신장 트리 중 가중치 합이 가장 최소인 최소 신장 트리
- 신장 트리 중 간선의 가중치 합이 최소인 트리
- 예제)
- 도시마다 도로를 짓는데 최소 거리가 되도록 구축
- 집마다 전화망 설치하는데 최소 비용이 되도록 설계
🔎 최소 신장 트리 알고리즘
그래프에서 최소 신장 트리를 만드는 대표적인 알고리즘 2개가 있다. 첫 번째는 크루스칼 알고리즘, 두 번째는 프림 알고리즘이다.
크루스칼(kruskal) 알고리즘
그래프의 간선을 하나씩 늘리며 MST를 만든다. 간선을 늘릴 때 가중치가 최소인 간선부터 추가하는 탐욕법을 이용한다.
과정
1) 간선은 가중치를 기준으로 오름차순 정렬한다.
2) 간선을 하나씩 살핀다. 간선을 MST에 추가했을 때 MST에 사이클이 생기지 않으면 추가한다. 사이클이 생긴다면 다음 간선으로 넘어간다.
크루스칼 알고리즘에 대해 자세하게 알고 싶다면 다음 링크를 따라가면 된다.
-> 크루스칼(kruskal) 알고리즘 더 알아보기
프림(Prim) 알고리즘
그래프의 정점 하나씩 늘리며 MST를 만든다. 정점을 늘릴 때 정점과 연결된 간선의 가중치가 최소인 것부터 추가하는 탐욕법을 이용한다.
과정
1) 시작 정점을 고른다. 시작 정점을 MST에 추가한다.
2) 정점과 이어진 간선을 살핀다. 간선과 이어진 다음 정점이 MST에 있지 않다면 이 정점과 간선을 최소 힙에 추가한다.
3) 최소 힙에서 꺼낸 정점이 MST에 포함되어 있지 않다면 MST에 추가하고 2)를 진행한다. 만약 꺼낸 정점이 MST에 포함되어 있으면 넘어간다.
4) 최소 힙이 빌 때까지 3)을 반복한다.
프림 알고리즘에 대해 자세하게 알고 싶다면 다음 링크를 따라가면 된다.
-> 프림(Prim) 알고리즘 더 알아보기
