
✍깊이우선탐색(DFS)
"깊이우선탐색(Depth First Search) 이란 루트 노드에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법이다. "
그래프 탐색이란 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것이다. 예를 들어 특정도시에서 다른 도시로 갈 수 있는지, 전자회로에서 특정 단자와 단자가 서로 연결되어 있는지를 탐색하는 알고리즘이다.
또 다른 그래프 탐색 방법으로는 너비우선탐색이있다. 해당 알고리즘에 대한 포스팅은 "너비우선탐색 포스팅"에서 확인할 수 있다.
👆DFS에서의 노드 탐색 순서
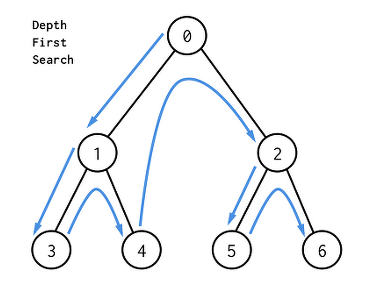
깊이우선탐색이기 때문에 한 방향으로 인접한 노드가 없을 때까지 (가장 깊은 노드까지) 탐색한 뒤 다른 방향으로 탐색을 하는 방식이다.
👆DFS의 특징
- 모든 노드를 탐색해야 할때 활용하기 좋은 방식이다.
- 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단하다.
- 단순 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느리다.
👆DFS 구현 알고리즘
- 루트노드에서 시작한다.
- 루트노드와 인접하고 방문된 적 없는 노드를 방문한다. (가장 깊은 노드까지)
- 인접하고 방문된 적 없는 노드가 없을 경우 (가장 깊은 노드를 방문한 뒤) 갈림길로 돌아와 다른 방향의 노드를 방문한다.
다음과 같은 순서를 따른다.
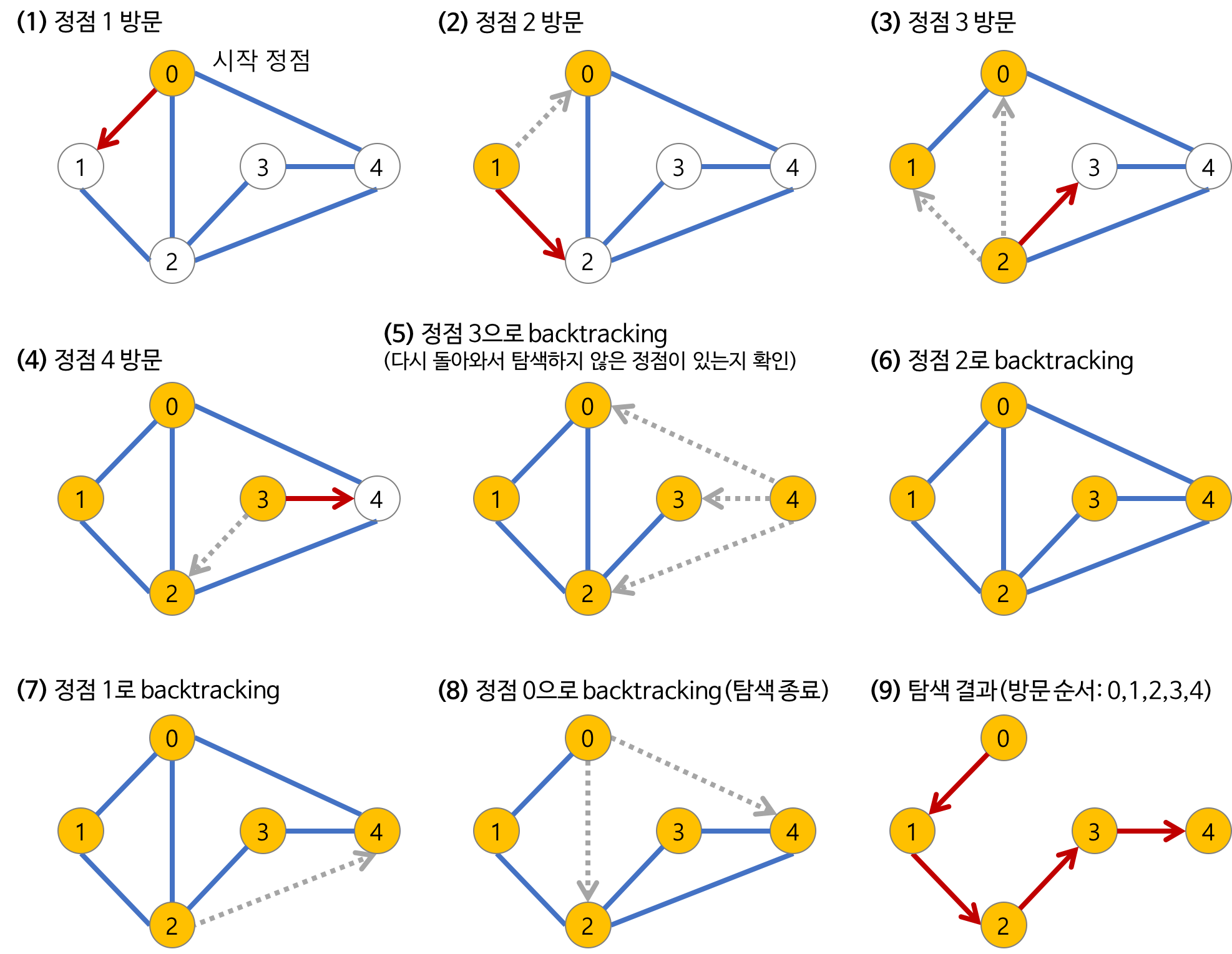
( 사진 출처: heejeong Kwon님의 기술블로그 )
위에서 설명한 3단계의 알고리즘으로 사진속의 과정을 설명하자면,
- (1)번에서 루트노드에 방문하고,
- (2)(3)(4)번에서 반복해서 인접하고, 방문된 적 없는 노드를 방문한다.
- 더 이상 인접하고, 방문된 적 없는 노드가 없는 경우 backtracking을통해 다른 방향 즉 탐색하지 않은 노드를 찾는다. (위의 예시에서는 존재하지 않음)
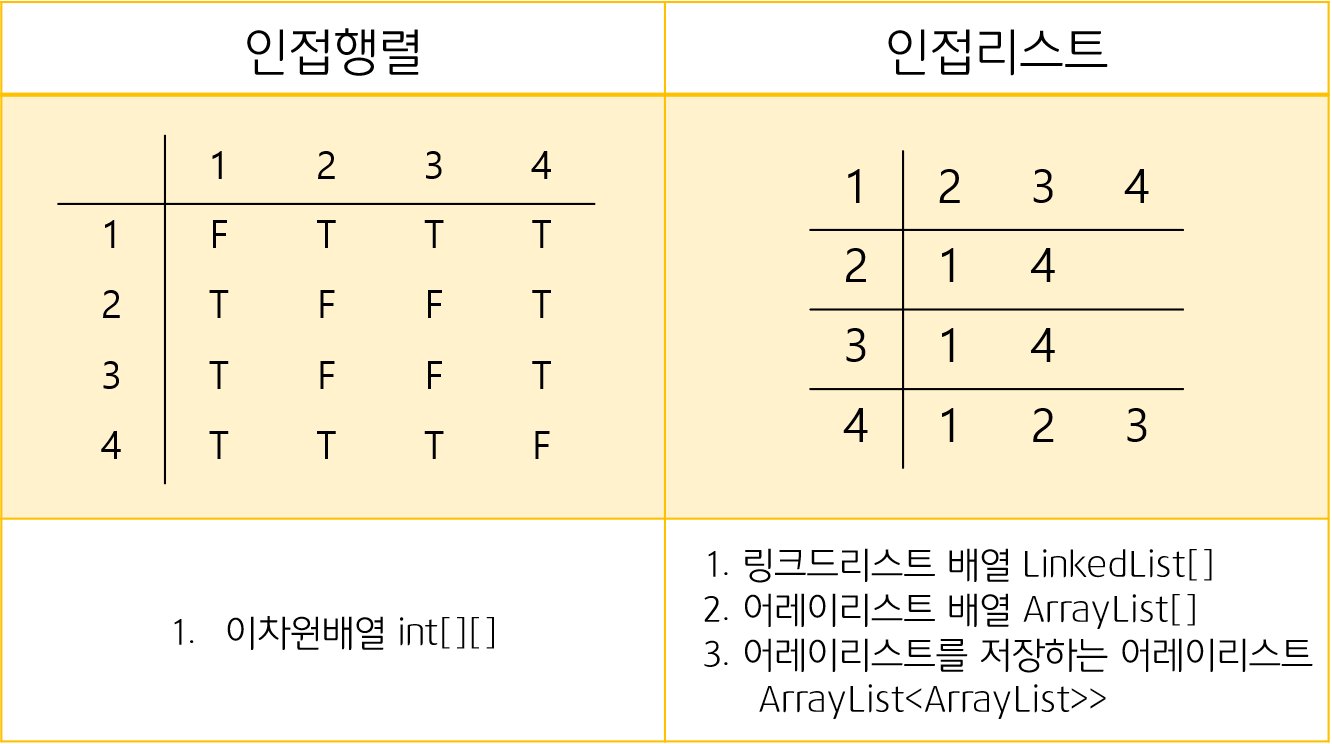
👆그래프 구현방식
- 인접행렬
- 인접리스트
예를 들어보자.

위와 같은 그래프를 구현할 때 다음과 같이 인접행렬과 인접리스트로 구현할 수 있다.
인접행렬은 이차원배열, 인접리스트는 링크드리스트 배열, 어레이리스트 배열, 어레이리스트를 저장하는 어레이리스트 등과 같은 방식으로 구현할 수 있다.
👆DFS를 인접행렬로 구현한 코드
인접행렬로 구현할 때 필요한 구조
- 인접행렬 배열 ( int[][] graph )
- 방문여부 배열 ( boolean[] DFSisVisited )
- 방문한 노드를 순서대로 저장하는 배열 ( ArrayList DFSvisitArr )
static void dfs(int node) {
DFSisVisited[node] = true; //노드방문여부를 true로 저장
DFSvisitArr.add(node); //방문한 노드를 순서대로 저장하는 리스트에 해당노드 추가
for( int i = 1 ; i <= nodeNum ; i++ ) {
//for문에서 backtracking을 수행한다.
if(graph[node][i] == 1 && DFSisVisited[i] == false) {
//인접, 방문된적X 를 만족하는 노드를 방문
dfs(i);
}
}
}- 인접행렬로 구현한 DFS의 시간복잡도 : O( N^2 )
👆DFS를 인접리스트로 구현한 코드
인접리스트로 구현할 때 필요한 구조
- 인접리스트 배열 ( ArrayList[] graph )
- 방문여부 배열 ( boolean[] DFSisVisited )
- 방문한 노드를 순서대로 저장하는 배열 ( ArrayList DFSvisitArr )
static void dfs(int node) {
DFSisVisited[node] = true; //노드방문여부를 true로 저장
DFSvisitArr.add(node); //방문한 노드를 순서대로 저장하는 리스트에 해당노드 추가
for( int i = 0 ; i < graph[node].size() ; i++ ) {
//for문에서 backtracking을 수행
int adjNode = graph[node].get(i);
if(DFSisVisited[adjNode] == false) {
//인접, 방문된적 없는 노드를 방문
//adjNode에는 인접노드만 저장되므로 인접조건O
dfs(adjNode);
}
}
} - 인접행렬로 구현한 DFS의 시간복잡도 : O( N + E )
