
✍너비우선탐색(BFS)
"너비우선탐색(Breadth First Search) 이란 루트 노드에서 시작해서 인접한 노드 를 먼저 탐색하는 방법이다. "
그래프 탐색이란 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것이다. 예를 들어 특정도시에서 다른 도시로 갈 수 있는지, 전자회로에서 특정 단자와 단자가 서로 연결되어 있는지를 탐색하는 알고리즘이다.
또 다른 그래프 탐색 방법으로는 깊이우선탐색이있다. 해당 알고리즘에 대한 포스팅은 "깊이우선탐색 포스팅"에서 확인할 수 있다.
👆BFS에서의 노드 탐색 순서
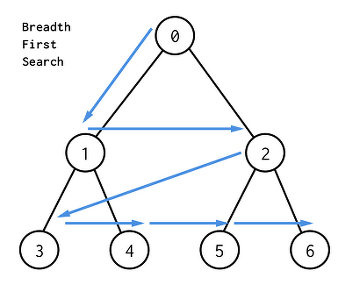
너비우선탐색이기때문에 깊이가 가장 얕은 노드부터 모두 탐색한뒤 깊이가 깊은 노드를 탐색하는 방법.
즉, 그림에서 깊이가 1인 노드1과 노드2를 먼저 탐색한뒤, 깊이가 1인 노드를 모두 탐색하였으므로 깊이가 2인 노드인 노드3, 노드4, 노드5, 노드6을 탐색하는 순서이다.
👆BFS의 특징
- 두 노드사이의 최단경로를 탐색할때 활용하기 좋은 방식이다. 멀리떨어진 노드는 나중에 탐색하는 방식이기 때문!
- 큐를 활용해서 탐색할 노드의 순서를 저장하고 큐에 저장된 순서대로 탐색한다. 선입선출의 방식을 활용해야 하기 때문에 큐를 활용한다.
👆BFS 구현 알고리즘
- 루트노드에서 시작한다.
- 루트노드와 인접하고 방문된적 없고, 큐에 저장되지 않은 노드를 Queue에 넣는다.
- Queue에서 dequeue하여 가장 먼저 큐에 저장한 노드를 방문한다.
다음과 같은 순서를 따른다.
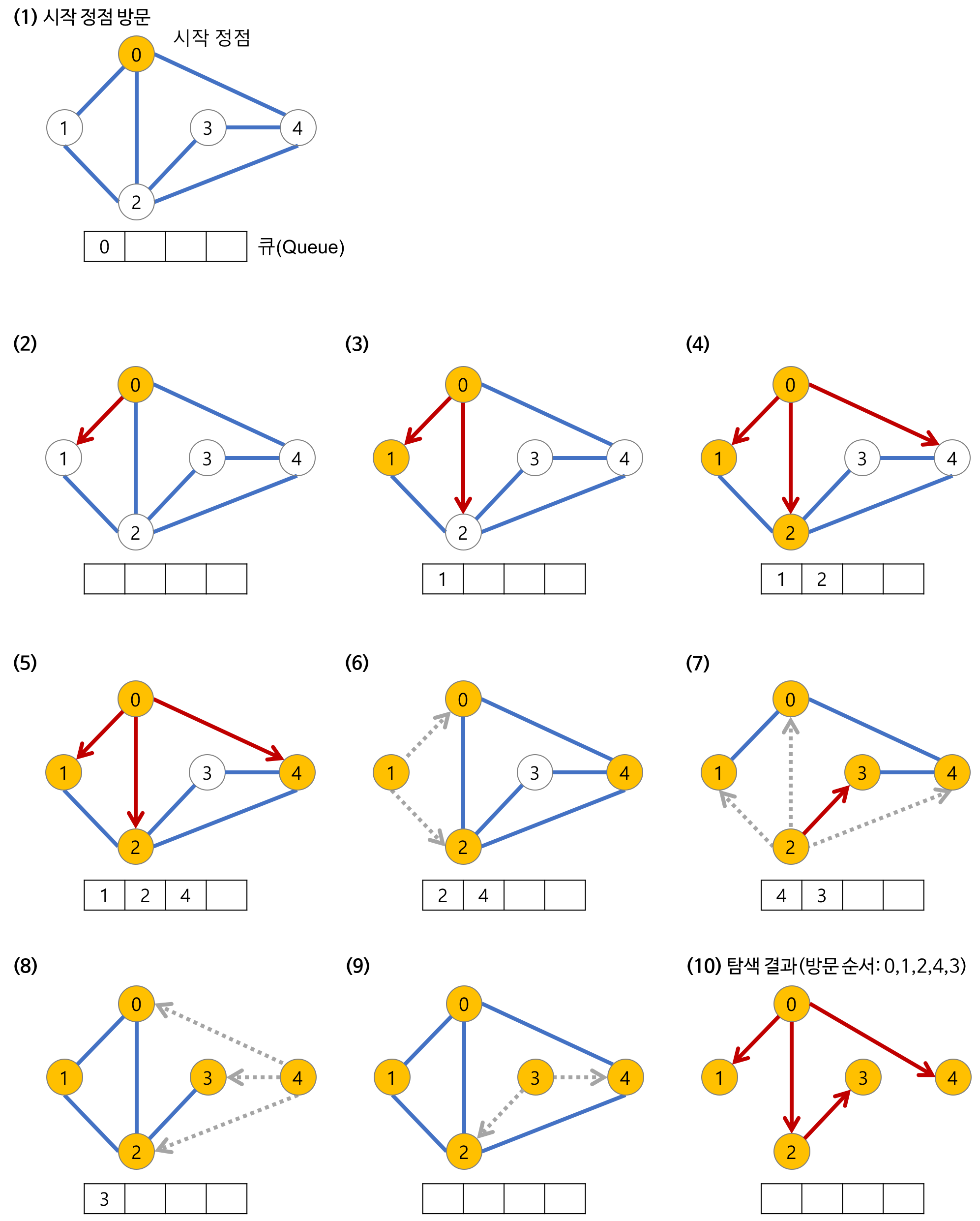
( 사진 출처: heejeong Kwon님의 기술블로그 )
위에서 설명한 3단계의 알고리즘으로 사진속의 과정을 설명하자면,
- (1)번에서 루트노드에 방문하고,
- (2)(3)(4)(5)에서 인접하고 방문된적 없으며 큐에 저장되지 않은 노드를 큐에 저장한다.
- (6)에서 가장먼저 큐에 저장된 1번 노드로 이동해서 인접노드들의 조건을 확인한다.
이 방식을 큐에 저장된 노드가 없을 때까지 반복한다.
👆그래프 구현방식
- 인접행렬
- 인접리스트
예를 들어보자.

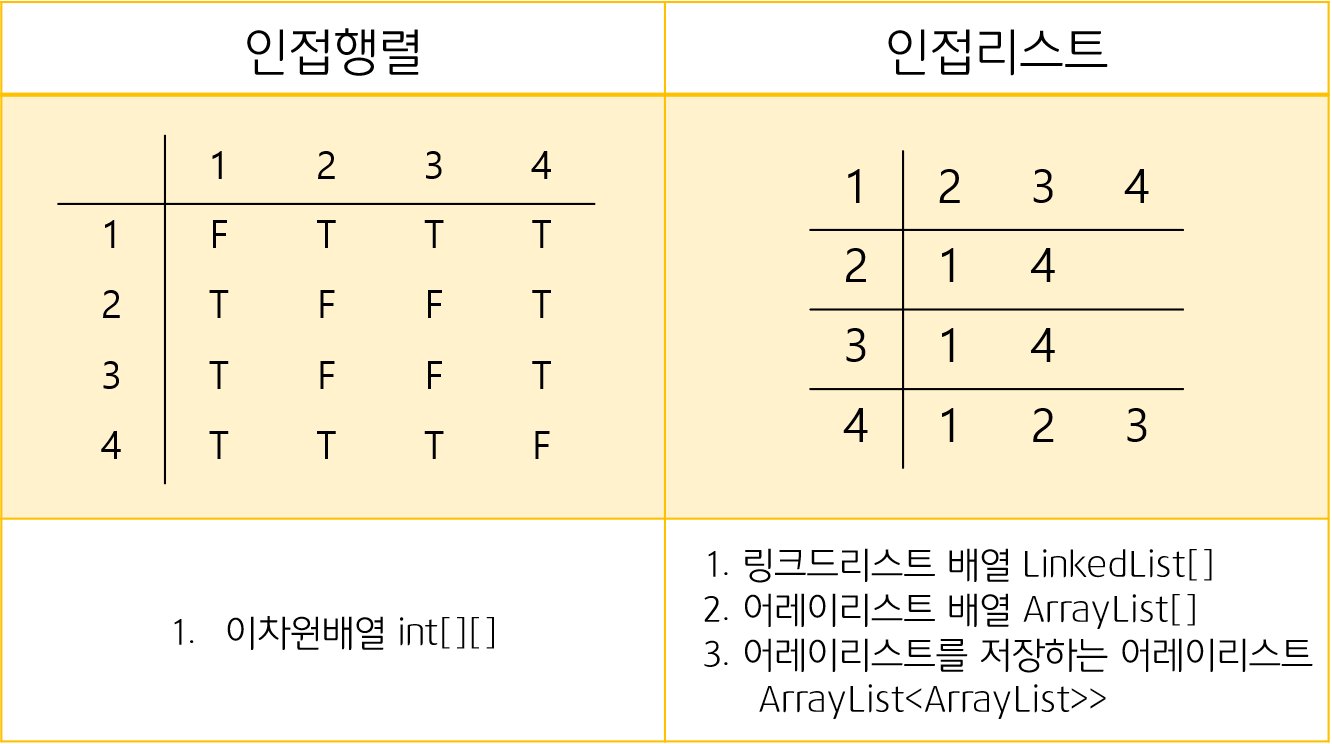
위와 같은 그래프를 구현할 때 다음과 같이 인접행렬과 인접리스트로 구현할 수 있다.
인접행렬은 이차원배열, 인접리스트는 링크드리스트 배열, 어레이리스트 배열, 어레이리스트를 저장하는 어레이리스트 등과 같은 방식으로 구현할 수 있다.
👆BFS를 인접행렬로 구현한 코드
인접행렬로 구현할 때 필요한 구조
- 인접행렬 배열 ( int[][] graph )
- 방문여부 배열 ( boolean[] BFSisVisited )
- 큐 ( Queue queue )
- 방문한 노드를 순서대로 저장하는 배열 ( ArrayList BFSvisitArr )
static void bfs(int node) {
BFSisVisited[node] = true; //노드방문여부를 true로 저장
BFSvisitArr.add(node); //방문한 노드를 순서대로 저장하는 리스트에 해당노드 추가
for( int i = 1 ; i <= nodeNum ; i++) {
if( graph[node][i] == 1 && BFSisVisited[i] == false && queue.contains(i)==false) {
//인접, 방문된적X, 큐에저장되지X 를 만족하는 노드를 큐에 추가
queue.add(i);
}
}
if(!queue.isEmpty())
bfs(queue.poll()); //큐에 가장 먼저 저장한 노드를 방문
}- 인접행렬로 구현한 BFS의 시간복잡도 : O( N^2 )
👆BFS를 인접리스트로 구현한 코드
인접리스트로 구현할 때 필요한 구조
- 인접리스트 ( ArrayList[] graph )
- 방문여부 배열 ( boolean[] BFSisVisited )
- 큐 ( Queue queue )
- 방문한 노드를 순서대로 저장하는 배열 ( ArrayList BFSvisitArr )
static void bfs(int node) {
BFSisVisited[node] = true; //노드방문여부를 true로 저장
BFSvisitArr.add(node); //방문한 노드를 순서대로 저장하는 리스트에 해당노드 추가
for( int i = 0 ; i < graph[node].size() ; i++ ) {
//graph[node]에 인접한 노드만 저장되어있음
int adjNode = graph[node].get(i);
if(BFSisVisited[adjNode] == false && queue.contains(adjNode) == false) {
//방문된적X, 큐에저장되지X 를 만족하는 노드를 큐에 추가
//adjNode에는 인접노드만 저장되므로 인접조건O
queue.add(adjNode);
}
}
if(!queue.isEmpty())
bfs(queue.poll()); //큐에 가장 먼저 저장한 노드를 방문
}- 인접리스트로 구현한 BFS의 시간복잡도 : O( N + E )
