이상치 처리 방법론

이상치 처리 방법론

• 이상치를 제거하는 방법은 여러가지가 존재한다.
• 다양한 방법중에서 아래 진행하는 과정은 데이터를 분석함수로써 모델링하는 방법이다.
  • 예를 들면 정규분포(=가우스 분포)로 특정 확률보다 작은 모든 값들을 찾고 제거하는 과정을 확신이 들때 까지 반복하는 과정이다.

---

직접 구현

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.stats import multivariate_normal as mn
from sklearn.neighbors import LocalOutlierFactor

d1 = np.loadtxt("outlier_1d.txt")
d2 = np.loadtxt("outlier_2d.txt")
d3 = np.loadtxt("outlier_curve.txt")
print(d1.shape, d2.shape, d3.shape)![](https://velog.velcdn.com/images/suminwooo/post/2b5feb2c-277c-4246-8e60-712c8bf48d32/image.zip)

# 결과
(1010,) (1010, 2) (1000, 2)

d1의 경우 1차원, d2, d3는 2차원 데이터

plt.scatter(d1, np.random.normal(7,0.2,size=d1.size),s=1, alpha=0.5)
plt.show()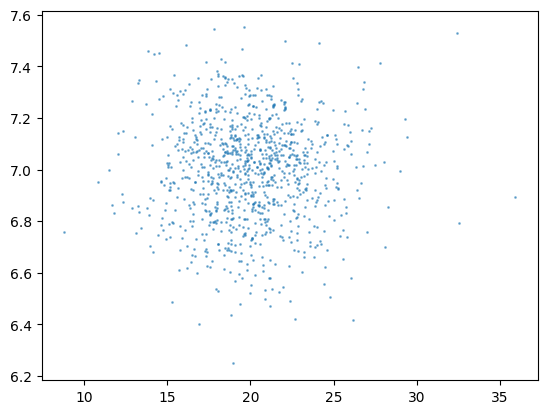

plt.scatter(d2[:,0],d2[:,1])
plt.show()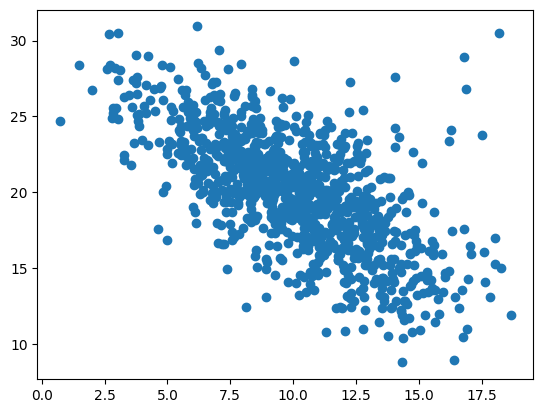

plt.plot(d3[:,0],d3[:,1])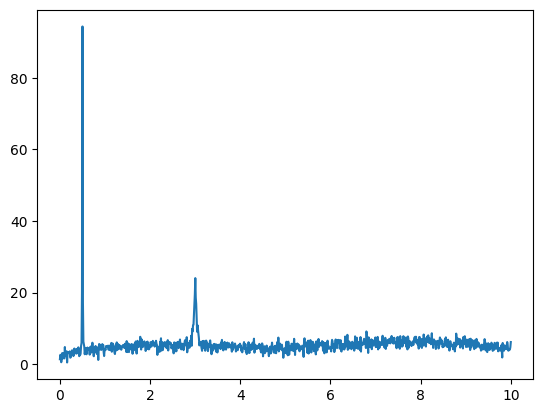

위의 3개의 값 d1, d2, d3 이상치 확인 방법을 아래에서 실행예정

---

# 기본적으로 데이터가 정규분포를 따른다고 가정
mean, std = np.mean(d1), np.std(d1)
z_score = np.abs((d1-mean)/std) 
threshold = 3 # z-score가 3 이상이면 모두 제거하도록 임계값 설정(변경하면서 진행)
good = z_score < threshold

Z-Score : 각 데이터 값이 평균으로부터 얼마나 떨어져 있는지를 나타내는 표준편차 숫자이다. Z-Score가 0이면 정확히 평균에 해당한다.

print(f"Rejection {(~good).sum()} points")
print(f"z-score of 3 corresponds to a prob of {100 * 2 * norm.sf(threshold):0.2f}%")
visual_scatter = np.random.normal(size=d1.size)
plt.scatter(d1[good], visual_scatter[good], s=2, label="Good", color = "#4CAF50")
plt.scatter(d1[~good], visual_scatter[~good], s=2, label="Bad", color = "#F44336")
plt.legend()

# result 
Rejection 5 points
z-score of 3 corresponds to a prob of 0.27%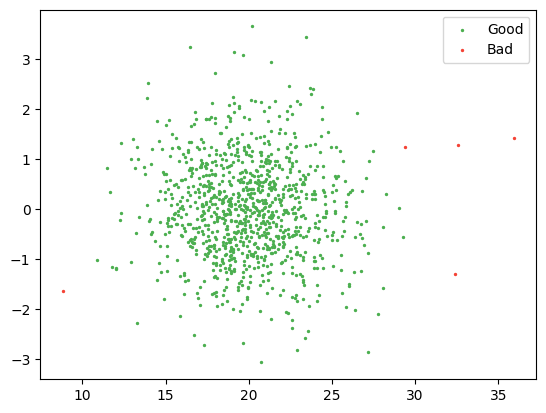

여기서 5개의 점이 z-score로 설정한 3보다 크기 때문에 Bad로 표현된다.

# d2의 분포를 2차원 가우스로 정량화
mean, cov = np.mean(d2, axis=0), np.cov(d2.T) 
good = mn(mean, cov).pdf(d2) > 0.01 / 100

• scipy.stats에서 다변수정규분포를 위한 multivariate_normal() 함수 제공
• pdf는 특정 구간에 속할 확률을 계산하기 위한 함수

plt.scatter(d2[good,0], d2[good,1], s=2, label="Good", color = "#4CAF50")
plt.scatter(d2[~good, 0], d2[~good,1], s=2, label="Bad", color = "#F44336")
plt.legend()
plt.show()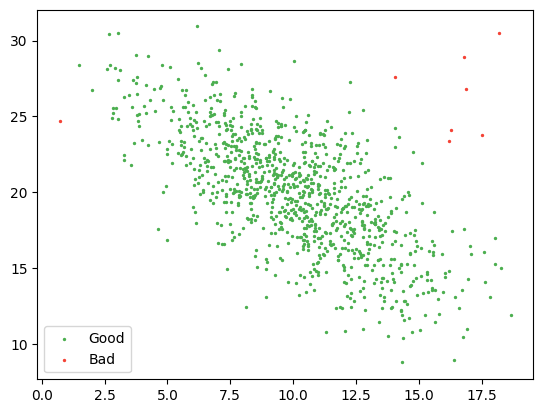

여기서도 몇 개의 데이터들이 good으로 설정한 값보다 크므로 Bad로 표현 된다.

xs, ys = d3.T
p = np.polyfit(xs, ys,deg=5)
ps = np.polyval(p, xs)

• numpy.polyfit 함수는 주어진 데이터에 대해 최소 제곱을 갖는 다항식 피팅을 반환한다. -> 위에서는 5차원 다항식을 출력
• numpy.polyval 함수는 입력 배열을 다항식으로 간주하고, 입력값을 넣어 계산된 값을 반환한다.

plt.plot(xs, ys, ".", label="Data")
plt.plot(xs, ps, label="poly fit")
plt.legend()
plt.show()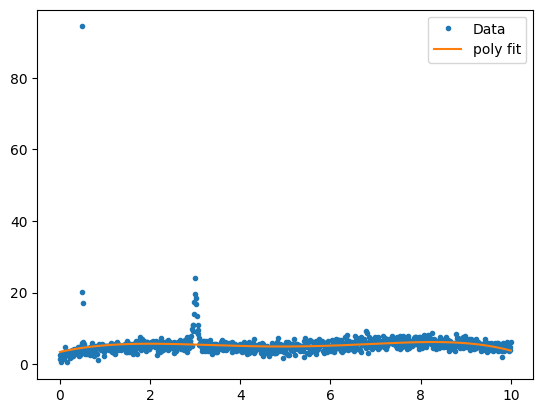

주황색 선이 데이터로 예측한 5차 다항식으로 표현이 된다.

• 처음에 언급한 부분처럼 이제 위에서 했던 방식을 for문을 통해 반복이 가능하다.

x, y = xs.copy(), ys.copy()
for i in range(5):
    p = np.polyfit(x,y,deg=5)
    ps = np.polyval(p,x)
    good = y-ps < 3 # only remove positive outliers
    
    x_bad, y_bad = x[~good], y[~good]
    x,y = x[good], y[good]
    
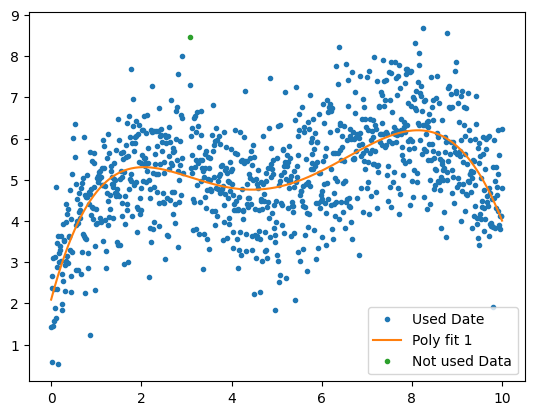
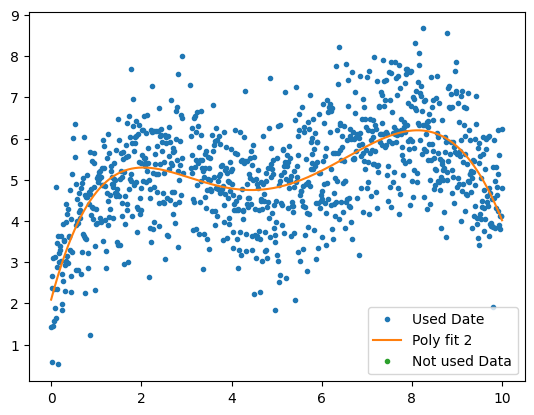
    plt.plot(x,y,".", label = "Used Date")
    plt.plot(x,np.polyval(p,x), label=f"Poly fit {i}")
    plt.plot(x_bad, y_bad, ".", label="Not used Data")
    plt.legend()
    plt.show()
    
    if (~good).sum() == 0:
        break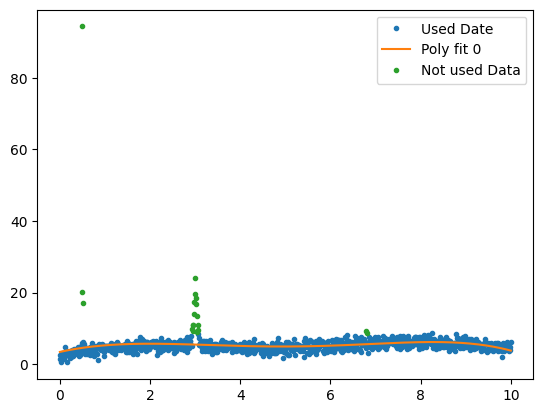

---

라이브러리 활용

• 직접구현 하는 방법도 존재하지만, 실제로는 sklearn에 구현이 되어 있다.(링크)

lof = LocalOutlierFactor(n_neighbors=20, contamination=0.05)
good = lof.fit_predict(d2) == 1
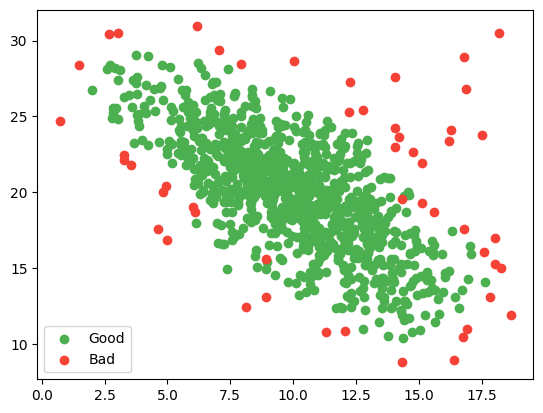
plt.scatter(d2[good, 0], d2[good ,1], label="Good", color="#4CAF50")
plt.scatter(d2[~good, 0], d2[~good ,1], label="Bad", color="#F44336")
plt.legend()

LocalOutlierFactor 내부의 contamination의 경우에는 위에서 설정한 임계값을 설정해주는 변수이다.

---

• 참고 : 유데미 - 【한글자막】 Python : 통계 분석을 위한 파이썬