변수의 조합
- 여러 개의 변수를 조합함으로써 변수 간 상호작용을 표현하는 특징을 만들 수 있다.
- 다만, 변수끼리 기계적으로 무작정 조합하면 의미가 없는 변수가 대량으로 생성된다. 이떄는 데이터에 관한 배경 지식을 활용하여 어떤 식의 조합이 의미가 있을지 연구하고 특징을 만들어 나간다.
- 수치형 변수 X 범주형 변수
- 범주형 변수의 레벨별로 수치형 변수의 평균이나 분산과 같은 통계량을 취해 새로운 특징으로 삼을 수 있다.
- 수치형 변수 X 수치형 변수
- 수치형 변수를 사칙연산하여 새로운 특징을 만들 수 있다.
- 그 밖에도 나머지 값을 구하는 연산이나 두 개의 변수가 같은지 여부를 확인하는 연산도 생각해볼 수 있다.
- 범주형 변수 X 범주형 변수
- 여러개의 범주형 변수를 조합하여 새로운 범주형 변수로 만들 수 있다.
범주형 변수를 서로 조합하여 만든 변수를 변환할 때는 타깃 인코딩이 효과적이다. 목적변수의 평균을 계산하는 그룹이 더 세분화되는 만큼, 더 특징적인 일련의 경향을 파악할 가능성이 높아지기 떄문이다.
- 행의 통계량 구하기
- 행의 방향, 즉 행 데이터별로 여러 변수의 통계량을 구하는 방법이 있다.
집약하여 통계량 구하기
- 일대다 대응하는 데이터를 집약하여 특징 만들기
단순 통계량 구하기
- 카운트(행 데이터 수)
- 카운트(유 일값 수) : 행의 수가 아닌 종류의 수를 특징으로 삼는 방법
- 존재 여부 : 로그인 오류가 있는지, 특정 페이지를 방문한 기록이 있는 지 등 어떤 종류의 로그가 존재하는지 여부를 두개 값을 갖는 이진변수로 나타내는 방법
- 합계, 평균, 비율
- 최대, 최소, 표준편차, 중앙값, 분위점, 첨도, 왜곡도
시간 정보 통계량 구하기
- 최초 또는 최근 행 데이터의 정보
- 간격 또는 빈도 정보
- 포인트 시점, 이벤트 발생 간격, 다음 행 데이터의 정보
- 순서, 추이, 동시출현, 연속 관련 정보
- 2가지 행동 중에 먼저 발생한 행동
- 연속되는 행동의 종류를 조합해 카운팅
- 특정 웹페이지의 열람 추이나 체류 시간 등
- 동시 구매 상품, 대체 구매 상품
- 3일 이상 연속 로그인 여부, 연속 로그인한 일수의 최댓값 등
조건 변경하기
- 특정 행동이나 특정 시간대의 움직임에 주목하는 등 조건을 바꾸어가며 통계량을 구할 수 있다.
- 특정 종류의 로그 조건 설정
- 집계 대상의 시간 및 기간 조건 설정
집계 단위 변경하기
- 사용자 id 단위뿐만 아니라 소속 그룹 단위로도 집계할 수 있다.
아이템이나 이벤트에 주목하기
- 아이템 또는 이벤트 중심으로 로그 집계
- 아이템 중심으로 그룹화
- 특별 상품에 주목
- 아이템 중심의 특징 생성
시계열 데이터 처리
- 시계열 데이터에는 특유의 성질이나 주의점이 있어서, 시간적인 정보를 적절하게 다루지 않을 경우 본래대로라면 예측에 사용할 수 없는 정보를 이용해 특징을 만들어버릴 때도 있다.
시계열 데이터란?
- 시간의 추이와 함께 순차적으로 관측한 데이터
- 시계열 데이터를 다루는 방식은 다음과 같은 관점에서 파악
- 시간 정보를 가지는 변수가 있는지 여부
: 적절히 활용해 특징을 만들 수 있음 - 학습 데이터와 테스트 데이터가 시계열로 나뉘어 있는지, 시간에 따라 분할라고 검증해야 할지 여부
:시간에 따라 분할한 검증을 실시함과 동시에 특징에 관해서도 미래 정보를 부적절하게 사용하지 않도록 주의해야함 - 사용자나 매장 등 계열별로 목적변수가 있는지, lag 특징을 취할 수 있는 형식이 있는지 여부
- 시간 정보를 가지는 변수가 있는지 여부
와이드 포맷과 롱 포맷 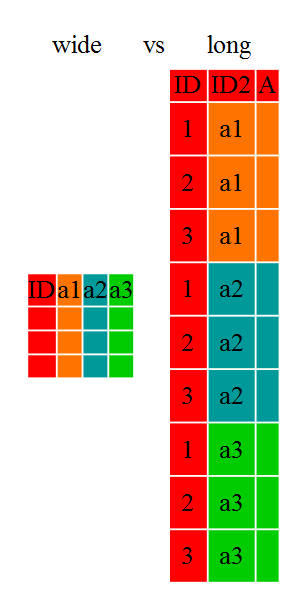
-
와이드 포맷은 주목 대상 변수만 유지할 수 있지만, 해당 변수의 시계열적인 변화를 알아보기 쉽고 lag 특징을 구할 때 다루기 쉽다. 한편 학습을 진행할 때는 날짜와 사용자벼로 목적변수를 가지는 롱 포맷으로 만들어야 한다.
-
롱 포맷으로 주어진 데이터를 와이드 포맷으로 변환한 뒤에 특징을 만들고, 변환된 데이터를 다시 롱 포맷으로 변환해 특징을 부가한 뒤 학습을 실시하는 경우가 있으므로 이러한 포맷 전환해 익숙해져야 한다.
-
pandas에서 데이터를 다룰 경우
- wide -> long : stack method
- long -> wide : pivot method
# 와이드 포맷, 롱 포맷
# -----------------------------------
# 와이드 포맷의 데이터 읽기
df_wide = pd.read_csv('../input/ch03/time_series_wide.csv', index_col=0)
# 인덱스의 형태를 날짜형으로 변경
df_wide.index = pd.to_datetime(df_wide.index)
print(df_wide.iloc[:5, :3])
'''
A B C
date
2016-07-01 532 3314 1136
2016-07-02 798 2461 1188
2016-07-03 823 3522 1711
2016-07-04 937 5451 1977
2016-07-05 881 4729 1975
'''
# 롱 포맷으로 변환
df_long = df_wide.stack().reset_index(1)
df_long.columns = ['id', 'value']
print(df_long.head(10))
'''
id value
date
2016-07-01 A 532
2016-07-01 B 3314
2016-07-01 C 1136
2016-07-02 A 798
2016-07-02 B 2461
2016-07-02 C 1188
2016-07-03 A 823
2016-07-03 B 3522
2016-07-03 C 1711
2016-07-04 A 937
...
'''
# 와이드 포맷으로 되돌림
df_wide = df_long.pivot(index=None, columns='id', values='value')lag 특징
- 단순한 lag 특징
- shift 함수를 이용하면 시간적으로 변경된 값을 구하여 lag 특징을 만들 수 있다.
# x는 와이드 포맷의 데이터 프레임
# 인덱스 = 날짜 등의 시간, 열 = 사용자나 매장 등, 값 = 매출 등 주목 대상 변수를 나타냄
# 1일 전의 값을 획득
x_lag1 = x.shift(1)
# 7일 전의 값을 획득
x_lag7 = x.shift(7)- 이동 평균과 기타 lag 특징
- 평균, 최댓값, 최솟값, 중앙값 등 다양한 통계량 이용 가능
# shift() 함수로 각각의 날짜 데이터 값을 일정 기간 전의 데이터로 치환(여기서는 1일전)
# 첫 번째 행은 이전 날짜가 없어 NaN(빈 값)이 됨. 두 번째부터는 전날 데이터로 치환
# 변환된 데이터 기준으로 rolling() 함수를 이용. window=3(자신을 포함하여 3개 행)
# 3일 범위의 날짜 기간(자신 포함 이전 3일)의 데이터 평균을 구함. 단, NaN이 하나라도 포함되면 NaN 반환
# 1기전부터 3기간의 이동평균 산출
x_avg3 = x.shift(1).rolling(window=3).mean()
# 모든 날짜를 1일 이전 데이터로 치환한 뒤,
# 변환된 데이터의 지정 시점부터 이전 날짜의 7일간의 범위에서 최댓값을 산출
x_max7 = x.shift(1).rolling(window=7).max()
# 7일 이전, 14일 이전, 21일 이전, 28일 이전의 합의 평균으로 치환
x_e7_avg = (x.shift(7) + x.shift(14) + x.shift(21) + x.shift(28)) / 4.0- 과거 데이터의 집계 허용 범위
- 얼마나 먼 과거의 데이터까지 집계해서 평균을 구해야 하는지는 데이터의 성질에 따라 달라지므로 매번 확인해야 한다.
- 오래된 정보 위주로 집계하면 최근 상황이 드러나지 않는 평균이 될 수 있다. 한편 장기간에 걸쳐 경향이 크게 변하지 않는 데이터라면 아예 장기간의 범위를 집계하는 편이 유리할 때도 있다.
- 그 밖에도 더 최신 정보를 가중치를 두는 가중이동평균이나 지수평활평균을 적용하는 방법도 있다.
- 다양한 단위나 조건으로 집계하여 lag 특징 생성
- 매장의 과거 매출뿐만 아니라 그 매장이 위치한 지역의 매출 평균과 같이 그룹화하여 집계 결과로 lag특징을 만들 수 있다.
- 목적변수 이외의 lag 특징 생성
- 목적 변수가 아닌 변수의 시차를 특징으로 취할 수도 있다. 예를 들어 매출과 함께 그 날의 날씨도 부여될 수 있다.
시점 관련 특징 생성
- 데이터를 예측하는 시점보다 과거 정보만을 사용한다는 제약을 지키면서 학습하고 예측하려면, 시점과 연계된 특징을 만들고 해당 시점을 키로 삼아 학습 데이터와 결합하는 방법도 있다.
- 특징을 생성하는 원본 데이터으 ㅣ집계 등을 통해 시점별 연계 변수를 구한다.
- 필요에 따라 누적합이나 이동평균을 구하거나 다른 변수와의 차 또는 비율을 구하는 식의 처리를 한다.
- 시점을 키로 삼아 학습 데이터와 결합한다.
예측용 데이터의 기간
- 특징 생성에 필요한 과거 기간
: 테스트 데이터의 기간이 1개월일 때 분할 시점 직후의 데이터에서는 하루 전의 목적 변수를 참조할 수 있지만, 한 달 후의 데이터에서는 한 달 전의 목적변수만 참조할 수 있다. 이런 경우 접근 방법 중 하나는 테스트 데이터의 기간이 분할 시점으로부터 며칠 앞에 있는지에 따라 개별적으로 모델을 만드는 방법이다. 즉, 분할 시점의 다음날 데이터에서는 1일 전의 lag 특징을 사용할 수 있으므로, 그 전제로 특징을 만들어 모델의 학습/검증/테스트 데이터 예측을 실시한다. 한편 분할 시점으로부터 1개월 후의 데이터로는 1개월 전의 lag 특징만 사용할 수 있다는 전제하에 마찬가지로 특징 및 모델을 만들고 예측한다.
차원축소와 비지도 학습의 특징
주성분분석(PCA; principal component analysis)
- 차원 축소의 가장 대표적인 기법
- 다차원 데이터를 분산이 큰 방향에서부터 순서대로 축을 다시 잡는 방법으로, 변수간 종속성이 클수록 더 소수의 주성분으로 원래 데이터를 표현할 수 있다. 다만 각 특징이 정규분포를 따르는 조건을 가정하므로, 왜곡된 분포를 가진 변수 등을 주성분분석에 적용하는 건 그다지 적절하지 않다.
- 한편 차원축소로서 특잇값분해(SVD)는 PCA와 거의 같은 의미가 된다.
- 참고로, 주성분분석을 비롯한 차원축소 기법은 데이터 전체에 반드시 적용할 필요는 없으며 일부 열에만 적용하는 방법을 고려할 수 있다.
# PCA
from sklearn.decomposition import PCA
# 데이터는 표준화 등의 스케일을 갖추기 위한 전처리가 이루어져야 함
# 학습 데이터를 기반으로 PCA에 의한 변환을 정의
pca = PCA(n_components=5)
pca.fit(train_x)
# 변환 적용
train_x = pca.transform(train_x)
test_x = pca.transform(test_x)
# TruncatedSVD
from sklearn.decomposition import TruncatedSVD
# 데이터는 표준화 등의 스케일을 갖추기 위한 전처리가 이루어져야 함
# 학습 데이터를 기반으로 SVD를 통한 변환 정의
svd = TruncatedSVD(n_components=5, random_state=71)
svd.fit(train_x)
# 변환 적용
train_x = svd.transform(train_x)
test_x = svd.transform(test_x)음수 미포함 행렬 분해(NMF; non-negative matrix factorization)
- 음수를 포함하지 않은 행렬 데이터를, 음수를 포함하지 않은 행렬들의 곱의 형태로 만드는 방법
- 음수가 아닌 데이터에만 사용할 수 있지만 PCA와는 달리 벡터의 합 형태로 나타낼 수 있다.
# NMF
# -----------------------------------
# 비음수의 값이기 때문에 MinMax스케일링을 수행한 데이터를 이용
train_x, test_x = load_minmax_scaled_data()
# -----------------------------------
from sklearn.decomposition import NMF
# 데이터는 음수가 아닌 값으로 구성
# 학습 데이터를 기반으로 NMF에 의한 변환 정의
model = NMF(n_components=5, init='random', random_state=71)
model.fit(train_x)
# 변환 적용
train_x = model.transform(train_x)
test_x = model.transform(test_x)잠재 디리클레 할당(LDA; latent Dirichlet allocation)
- 자연어 처리에서 문서를 분류하는 토픽모델에서 쓰이는 기법으로 확률적 생성 모델의 일종
# -----------------------------------
# MinMax스케일링을 수행한 데이터를 이용
# 카운트 행렬은 아니지만, 음수가 아닌 값이면 계산 가능
train_x, test_x = load_minmax_scaled_data()
# -----------------------------------
from sklearn.decomposition import LatentDirichletAllocation
# 데이터는 단어-문서의 카운트 행렬 등으로 함
# 학습 데이터를 기반으로 LDA에 의한 변환을 정의
model = LatentDirichletAllocation(n_components=5, random_state=71)
model.fit(train_x)
# 변환 적용
train_x = model.transform(train_x)
test_x = model.transform(test_x)선형판별분석(LDA; linear discriminant analysis)
- 지도 학습의 분류 문제에서 차원축소를 실시하는 방법
- 학습 데이터를 잘 분류할 수 있는 저차원의 특징 공간을 찾고, 원래 특징을 그 공간에 투영함으로써 차원을 줄인다.
- 즉, 학습 데이터가 n행의 행 데이터와 f개의 특징으로 이루어진 nXf행렬이라 할 때 fXk의 변환행렬을 곱함으로써 nXk행렬로 변환한다. 또한 차원축소 후의 차원 수 k는 클래스 수보다 줄어들고, 이진 분류일 때는 변환 후에 1차원 값이 된다.
# LinearDiscriminantAnalysis
# -----------------------------------
# 표준화된 데이터를 사용
train_x, test_x = load_standarized_data()
# -----------------------------------
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
# 데이터는 단어-문서의 카운트 행렬 등으로 함
# 학습 데이터를 기반으로 LDA에 의한 변환을 정의
lda = LDA(n_components=1)
lda.fit(train_x, train_y)
# 변환 적용
train_x = lda.transform(train_x)
test_x = lda.transform(test_x)t-SNE
- 차원축소의 비교적 새로운 방법
- 데이터를 2차원 평면상에 압축하여 시각화 목적으로 쓰일때가 많다. 원래의 특징 공간상에서 가까운 점이 압축 후에 2차원 평면으로 표현될 때도 가깝게 표한된다.
- 비선형 관계를 파악할 수 있으므로, 원래의 특징에 이들 t-SNE로 압축 결과를 더하면 모델 성능이 올라갈 수 있다. 다만 계산 비용이 높으며 2차원 또는 3차원을 초과하는 압축에는 적합하지 않다.
# t-sne
# -----------------------------------
# 현 버전에 설치 이슈가 있어, 확인 중.
# 표준화된 데이터를 사용
train_x, test_x = load_standarized_data()
# -----------------------------------
import bhtsne
# 데이터는 표준화 등의 스케일을 갖추기 위한 전처리가 이루어져야 함
# t-sne에 의한 변환
data = pd.concat([train_x, test_x])
embedded = bhtsne.tsne(data.astype(np.float64), dimensions=2, rand_seed=71)UMAP
- t-SNE와 마찬가지로 원래의 특징 공간상에서 가까운 점이 압축 후에도 가까워지도록 표현
- 빠르며, 2차원이나 3차원을 넘는 압축도 가능
# UMAP
# -----------------------------------
# 표준화된 데이터를 사용
train_x, test_x = load_standarized_data()
# -----------------------------------
import umap
# 데이터는 표준화 등의 스케일을 갖추는 전처리가 이루어져야 함
# 학습 데이터를 기반으로 UMAP에 의한 변환을 정의
um = umap.UMAP()
um.fit(train_x)
# 변환 적용
train_x = um.transform(train_x)
test_x = um.transform(test_x)오토인코더
- 신경망을 이용한 차원 압축 방법
- 입력 차원보다 작은 중간층을 이용하여 입력과 같은 값으로 출력하는 신경망을 학습함으로써, 원래의 데이터를 재현할 수 있는 더 저차원의 표현을 학습한다.
군집화
- K-Means : 고속 계산할 때는 Mini-Batch K-Means도 사용
- DBSCAN
- 병합 군집 : 응집형 계층 클러스터링
# 클러스터링
# -----------------------------------
# 표준화된 데이터를 사용
train_x, test_x = load_standarized_data()
# -----------------------------------
from sklearn.cluster import MiniBatchKMeans
# 데이터는 표준화 등의 스케일을 갖추는 전처리가 이루어져야 함
# 학습 데이터를 기반으로 Mini-Batch K-Means를 통한 변환 정의
kmeans = MiniBatchKMeans(n_clusters=10, random_state=71)
kmeans.fit(train_x)
# 해당 클러스터를 예측
train_clusters = kmeans.predict(train_x)
test_clusters = kmeans.predict(test_x)
# 각 클러스터 중심까지의 거리를 저장
train_distances = kmeans.transform(train_x)
test_distances = kmeans.transform(test_x)기타 기법
- 위치 정보, 텍스트 데이터, 이미지 데이터 그리고 데이터 간의 관계성 등을 활용한 특징을 생성하고 이를 활용하는 다양한 기법
배경 메커니즘의 이해
- 특징을 생성하는 방법은 다양하며 그 모든 기법을 활용하면 무수히 많은 특징을 생성할 수 있다.
- 사용자 행동에 주목
- 사용자 성격, 행동 특징, 행동 사이클을 표현하는 특징 만들기
- 이용 목적의 클러스터로 나눠 생각하기
- 특정 상품에 대한 선호도가 있을지 생각하기
- 같은 물건을 이미 구매한 경우 등 행동 저해 요소는 없을지 생각하기
- 사용자가 웹사이트에서 어떤 식으로 화면을 이용하여 상품을 구매했는지 살펴보기
- 서비스 제공 측의 동향 주목
- 업계에서 주로 사용하는 분석 방법
- RFM 분석이라는 고객 분석 기법을 이용하여 사용자 분류와 특징을 생성(Recency: 최신 구매일, Frequency: 구매 빈도, Monetary: 구매 금액)
- 개인의 신용 리스크를 심사할 때 어떤 항목이 대상이 될 수 있을지 관련 단어로 조사
- 질병 진단 기준과 관련해 어떤 식의 점수 책정 방법이나 조건 분기 규칙으로 진단되는지, 어떤 특징과의 조합이 고려되는지 조사
- 여러 변수를 조합하여 지수 생성
- 신장이나 체중으로부터 BMI를 구하기너 기온 및 습도에서 불쾌지수를 구하는 등 여러 개의 변수를 조합한 지수를 작성하는 것도 유효할 수 있음
- 자연 현상의 메커니즘에 주목
상댓값에 주목
- 어떤 사용자의 값과 그 사용자가 속한 그룹의 평균값의 차이 또는 비율을 구하는 것처럼, 다른 값과 비교했을 때의 차이나 비율을 같은 상댓값에 주목하는 것도 효과적이다.
위치 정보에 주목
- 위도나 경도 등의 위치 정보가 데이터에 포함될 경우 위치 간 거리를 특징으로 고려할 수 있다. 그 밖에도 주요 도시나 랜드마크로부터의 거리를 계산하거나 지역 정보와 같은 외부 데이터를 결합하여 특징을 만들 수 있다.
참고 : 데이터가 뛰어노는 AI 놀이터, 캐글