1. 회귀의 평가 지표
- RMSE(root mean square error)
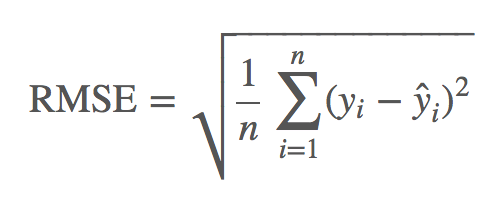
- RMSE의 값을 최소화했을 때의 결과가, 오차가 정규분포를 따른다는 전제하에 구할 수 있는 최대가능도방법과 같이지는 등 통계학적으로도 큰 의미를 가지는 평가 지표
- 하나의 대푯값으로 예측을 실시한다고 가정했을 때 평가지표 RMSE를 최소화하는 예측값이 평균값
- MAE와 비교하면 이상치의 영향을 받기 쉬우므로, 이상치를 제외처리 등을 미리 해두지 않으면 이상치에 과적합된 모델을 만들 가능성이 있다.
- RMSLE(root mean square logarithmic error)

- 목적변수의 분포가 한쪽으로 치우치면 큰 값의 영향력이 일반적인 RMSE보다 강해지기 때문에 이를 방지하고자 사용한다. 또한 실제값과 예측값의 비율을 측정 지표로 사용하고 싶은 경우에 사용한다.
- 로그를 취할때는 실젯값이 0일 때 그 값이 음으로 무한대 오류가 발생하므로 보통은 1을 더하고 나서 로그를 취한다.(numpy의 log1p 함수 활용 가능)
- MAE(mean absolute error)
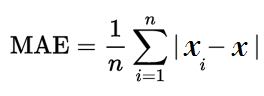
- MAE는 이상치의 영향을 상대적으로 줄여주는 평가에 적절한 함수이다.
- 하나의 대푯값으로 예측할 때 MAE를 최소화하는 예측값은 중앙값이다.
- 결정 계수(coefficient of determination)
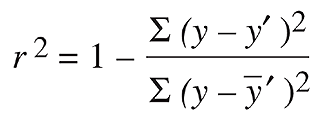
- 회귀 분석의 적합성을 나타낸다.
- 분모는 예측값에 의존하지 않고, 분자는 오차의 제곱에 관한 것이므로 이 지표의 최대화가 곧 RMSE의 최소화와 같다.
- 결정계수의 최대값은 1이므로 1에 가까워질수록 모델 성능이 높은 예측으로 볼 수 있다.
2. 이진 분류의 평가 지표
2-1. 각 행 데이터가 양성인지 음성인지를 예측값으로 삼아 평가하는 평가 지표
- 혼돈 행렬(confusion matrix)
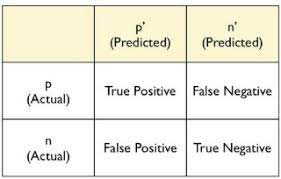
# 혼동행렬
from sklearn.metrics import confusion_matrix
# 0, 1로 표현되는 이진 분류의 실젯값과 예측값
y_true = [1, 0, 1, 1, 0, 1, 1, 0]
y_pred = [0, 0, 1, 1, 0, 0, 1, 1]
tp = np.sum((np.array(y_true) == 1) & (np.array(y_pred) == 1))
tn = np.sum((np.array(y_true) == 0) & (np.array(y_pred) == 0))
fp = np.sum((np.array(y_true) == 0) & (np.array(y_pred) == 1))
fn = np.sum((np.array(y_true) == 1) & (np.array(y_pred) == 0))
confusion_matrix1 = np.array([[tp, fp],
[fn, tn]])
print(confusion_matrix1)
# array([[3, 1],
# [2, 2]])
# 사이킷런의 metrics 모듈의 confusion_matrix로도 작성 가능하지만,
# 혼동행렬의 요소 배치가 다르므로 주의가 필요
confusion_matrix2 = confusion_matrix(y_true, y_pred)
print(confusion_matrix2)
# array([[2, 1],
# [2, 3]])- 정확도와 오류율(accurate, error rate)
- 불균형한 데이터의 경우 모델의 성능을 평가하기가 어려워 분석 경진 대회에서 평가지표로 많이 사용하지 않음
# 정확도(accuracy)
# -----------------------------------
from sklearn.metrics import accuracy_score
# 0, 1로 표현되는 이진 분류의 실젯값과 예측값
y_true = [1, 0, 1, 1, 0, 1, 1, 0]
y_pred = [0, 0, 1, 1, 0, 0, 1, 1]
accuracy = accuracy_score(y_true, y_pred)
print(accuracy)
# 0.625-
정밀도와 재현율(precision, recall)

- 정밀도 : 양성으로 예측한 값 중에서 실젯값도 양성일 비율
- 재현율 : 실젯값이 양성인 것 중에서 예측값이 양성일 비율
- 정밀도와 재현율은 어느 한 쪽의 값을 높이려 할 때 다른 쪽의 값은 낮아지는 트레이트 오프관계이다. 반대로 어느 한 쪽의 지표를 무시하면 다른 쪽 지표를 1에 가깝게 할 수 있다.
-
F1-score와 Fβ-score
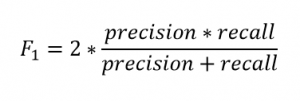
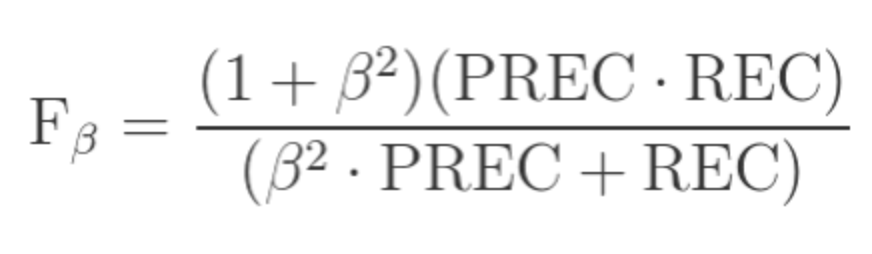
- F1-score는 정밀도와 재현율의 조화평균으로 계산되는 지표이다. 정밀도와 재현율의 균형을 이루는 지표는 실무에서도 자주쓰이며 F 점수(F score)라고도 한다.
- Fβ-score는 F1-score에서 구한 정밀도와 재현율의 균형(조화 평균)에서 계수 β에 따라 재현율에 가중치를 주어 조정한 지표이다.
-
매튜상관계수(MCC; Matthews correlation coefficient)

- 사용 빈도는 높지 않지만 불균형한 데이터의 모델 성능을 적절히 평가하기 쉬운 지표
- 이 지표는 -1(완전 반대 예측)에서 +1(완벽한 예측)사이의 범위를 가진다. (0일 경우 랜덤한 예측)
- F1-score와 달리 양성과 음성을 대칭 취급하므로 실젯값과 예측값의 양성과 음성을 서로 바꿔도 점수는 닽다.
2-2. 각 행 데이터가 양성일 확률을 예측값으로 삼아 평가하는 평가지표
- 로그 손실(=교차 엔트로피(cross-entropy))

- 로그 손실이 낮을 수록 좋은 지표
- 실제 값이 1이 될 확률을 1로 정확하게 예측할 때 로그 손실의 값이 최소가 된다.
- 이 지표는 모델을 학습시킬 때 목적함수로 자주 사용된다.
# logloss
# -----------------------------------
from sklearn.metrics import log_loss
# 0, 1로 나타나는 이진 분류의 실젯값과 예측 확률
y_true = [1, 0, 1, 1, 0, 1]
y_prob = [0.1, 0.2, 0.8, 0.8, 0.1, 0.3]
logloss = log_loss(y_true, y_prob)
print(logloss)
# 0.7136- AUC(area under the ROC curve, ROC 곡선 아래 면적)
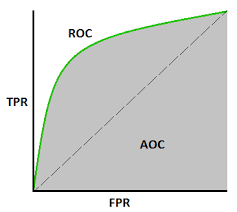
- ROC 곡선은 예측값을 양성으로 판단하는 임계값을 1에사 0으로 움직일 때의 거짓 양성 비율(FPR)과 참 양성 비율(TPR)을 그래프의 (x, y)축으로 나타낼 수 있다.
경진 대회에서 예측 모델의 성능을 겨루는 게 목적이라면 로그 손실이나 AUC처럼 확률값에 기반을 두는 편이 좋다. 하지만 실제로는 F1-score도 자주 쓰이는 만큼, 경제적으로 좋은 성적을 거두기 위해서는 이들 평가지표의 특징을 잘 이해하고 대응해야 한다.
2-3. 다중 클래스 분류의 평가 지표
- multi-class accuracy
- 이진 분류의 정확도를 다중 클래스로 확장한 것
- 예측이 올바른 비율을 나태내는 지표로, 예측이 정답인 행 데이터 수를 모든 행 데이터 수로 나눈 결과이다.
- multi-class logloss
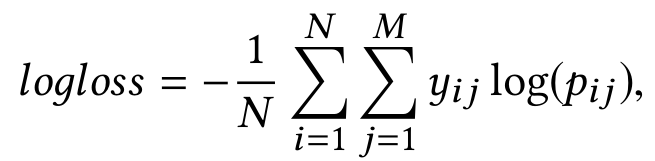
- 로그 손실을 다중 클래스 분류로 확장한 것으로, 다중 클래스 분류의 평가지표로 자주 쓰인다.
- 각 클래스의 예측 확률을 제출하고, 행 데이터가 속한 클래스의 예측 확률을 로그를 취해 부호를 반전시킨 값이 점이다.
# multi-class logloss
from sklearn.metrics import log_loss
# 3 클래스 분류의 실젯값과 예측값
y_true = np.array([0, 2, 1, 2, 2])
y_pred = np.array([[0.68, 0.32, 0.00],
[0.00, 0.00, 1.00],
[0.60, 0.40, 0.00],
[0.00, 0.00, 1.00],
[0.28, 0.12, 0.60]])
logloss = log_loss(y_true, y_pred)
print(logloss)
# 0.3626- mean-F1, macro-F1, micro-F1
- F1-score를 여러 클래스로 확장한 것이며 주로 다중 레이블 분류에서 사용하는 평가지표이다.
- mean-F1 : 행 데이터 단위로 F1-score를 계산하고 그 평균값이 평가 지표 점수
- macro-F1 : 각 클래스별 F1-score를 계산하고 이들의 평균값을 평가 지표로 삼는다.
- micor-F1 : 행 데이터 X 클래스의 각 쌍에 대해 TP, TN, FP, FN중 어디에 해당하는지를 카운트한다. 그 혼돈행렬에 근거하여 F 점수를 계산한 값이 평가지표 점수이다.
# mean_f1, macro_f1, micro_f1
from sklearn.metrics import f1_score
# 다중 레이블 분류의 실젯값·예측값은 평가지표 계산상으로는 행 데이터 × 클래스의 두
# 값 행렬로 해야 다루기 쉬움
# 실젯값 - [[1,2], [1], [1,2,3], [2,3], [3]]
y_true = np.array([[1, 1, 0],
[1, 0, 0],
[1, 1, 1],
[0, 1, 1],
[0, 0, 1]])
# 예측값 - [[1,3], [2], [1,3], [3], [3]]
y_pred = np.array([[1, 0, 1],
[0, 1, 0],
[1, 0, 1],
[0, 0, 1],
[0, 0, 1]])
# mean-f1는 행 데이터마다 F1-score를 계산하여 평균을 취함
mean_f1 = np.mean([f1_score(y_true[i, :], y_pred[i, :]) for i in range(len(y_true))])
# macro-f1에서는 행 데이터마다 F1-score를 계산하여 평균을 취함
n_class = 3
macro_f1 = np.mean([f1_score(y_true[:, c], y_pred[:, c]) for c in range(n_class)])
# micro-f1에서는 행 데이터 × 클래스의 쌍으로 TP/TN/FP/FN을 계산하여 F1-score를 구함
micro_f1 = f1_score(y_true.reshape(-1), y_pred.reshape(-1))
print(mean_f1, macro_f1, micro_f1)
# 0.5933, 0.5524, 0.6250
# scikit-learn 메소드를 사용하여 계산 가능
mean_f1 = f1_score(y_true, y_pred, average='samples')
macro_f1 = f1_score(y_true, y_pred, average='macro')
micro_f1 = f1_score(y_true, y_pred, average='micro')
print(mean_f1, macro_f1, micro_f1)- QWK(quadratic weighted kappa)
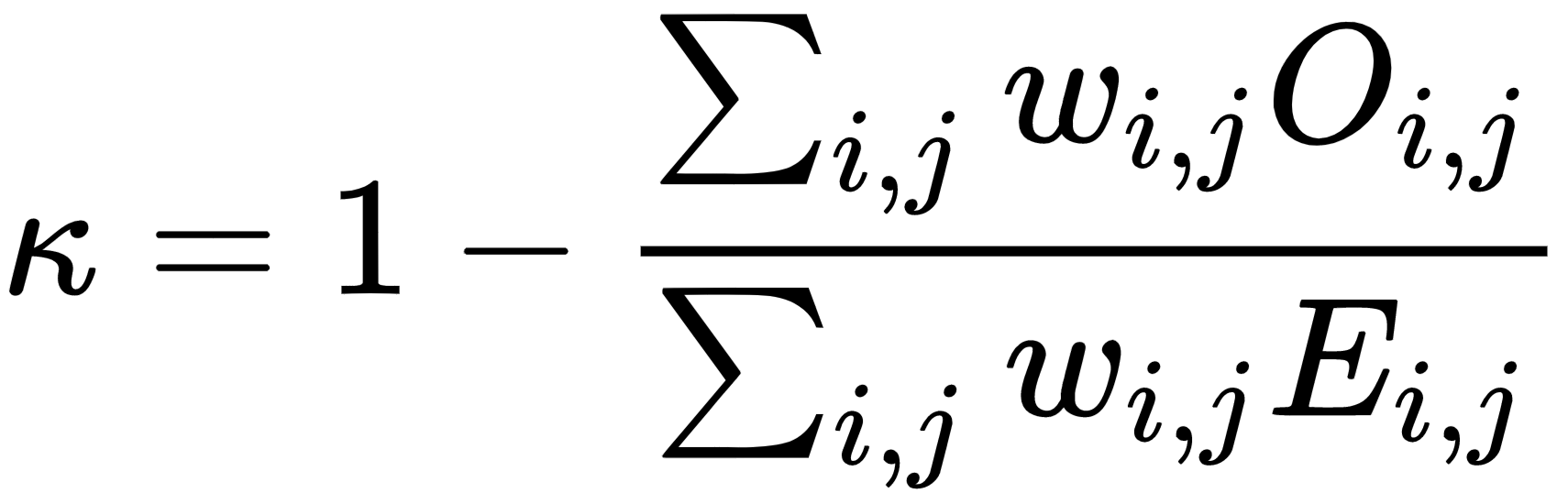
- 다중 클래스 분류에서 클래스 간에 순서 관계가 있을때(예를 들어 영화 평가에서 1~5점으로 점수를 매기는 경우) 사용한다.
# quadratic weighted kappa
from sklearn.metrics import confusion_matrix, cohen_kappa_score
# quadratic weighted kappa을 계산하는 함수
def quadratic_weighted_kappa(c_matrix):
numer = 0.0
denom = 0.0
for i in range(c_matrix.shape[0]):
for j in range(c_matrix.shape[1]):
n = c_matrix.shape[0]
wij = ((i - j) ** 2.0)
oij = c_matrix[i, j]
eij = c_matrix[i, :].sum() * c_matrix[:, j].sum() / c_matrix.sum()
numer += wij * oij
denom += wij * eij
return 1.0 - numer / denom
# y_true는 실젯값 클래스 목록, y_pred는 예측값 클래스 목록
y_true = [1, 2, 3, 4, 3]
y_pred = [2, 2, 4, 4, 5]
# 혼동행렬을 계산
c_matrix = confusion_matrix(y_true, y_pred, labels=[1, 2, 3, 4, 5])
# quadratic weighted kappa를 계산
kappa = quadratic_weighted_kappa(c_matrix)
print(kappa)
# 0.6154 (소수점 5번째자리 반올림)
# scikit-learn의 메소드로도 계산 가능
kappa = cohen_kappa_score(y_true, y_pred, weights='quadratic')
print(kappa)
# 0.6154 (소수점 5번째자리 반올림)- MAP@K(Mean Average Precision at (@) K)
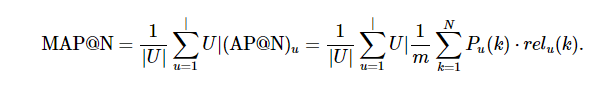
- 추천 문제에서 자주 사용되는 지표
- 각 행 데이터가 하나 또는 여러 클래스에 속할 때, 포함될 가능성이 높을 것으로 예측한 순서대로 K개의 클래스를 예측값으로 삼는다.
# MAP@K
# K=3、행의 수는 5개, 클래스는 4종류
K = 3
# 각 행의 실젯값
y_true = [[1, 2], [1, 2], [4], [1, 2, 3, 4], [3, 4]]
# 각 행에 대한 예측값 - K = 3이므로, 일반적으로 각 행에 각각 3개까지 순위를 매겨 예측
y_pred = [[1, 2, 4], [4, 1, 2], [1, 4, 3], [1, 2, 3], [1, 2, 4]]
# 각 행의 average precision을 계산하는 함수
def apk(y_i_true, y_i_pred):
# y_pred가 K이하의 길이이고 모든 요소가 달라야 함
assert (len(y_i_pred) <= K)
assert (len(np.unique(y_i_pred)) == len(y_i_pred))
sum_precision = 0.0
num_hits = 0.0
for i, p in enumerate(y_i_pred):
if p in y_i_true:
num_hits += 1
precision = num_hits / (i + 1)
sum_precision += precision
return sum_precision / min(len(y_i_true), K)
# MAP@K을 계산하는 함수
def mapk(y_true, y_pred):
return np.mean([apk(y_i_true, y_i_pred) for y_i_true, y_i_pred in zip(y_true, y_pred)])
# MAP@K을 요청
print(mapk(y_true, y_pred))
# 0.65
# 정답 수가 같아도 순서가 다르면 점수도 다름
print(apk(y_true[0], y_pred[0]))
print(apk(y_true[1], y_pred[1]))
# 1.0, 0.5833참고 : 데이터가 뛰어노는 AI 놀이터, 캐글