[Swift] 백준 9465 - 스티커

문제 링크

스티커들의 합의 최대 값을 구하면 된다.

처음엔 스티커의 max를 구해 그 값을sum에 더해주고
양 옆, 아래의 값들을 0 으로 바꿔주곤 했는데 이렇게 하면 값은 나오지만 시간초과가 나온다. (또한 dp도 사용하지 않은 방식이다)

따라서 다른 분들의 풀이를 보고 다음과 같은 개념을 발견했다.

1. 최대한 스티커를 빽뺵하게 많이 떼어야 최댓값을 얻을 수 있다.
   

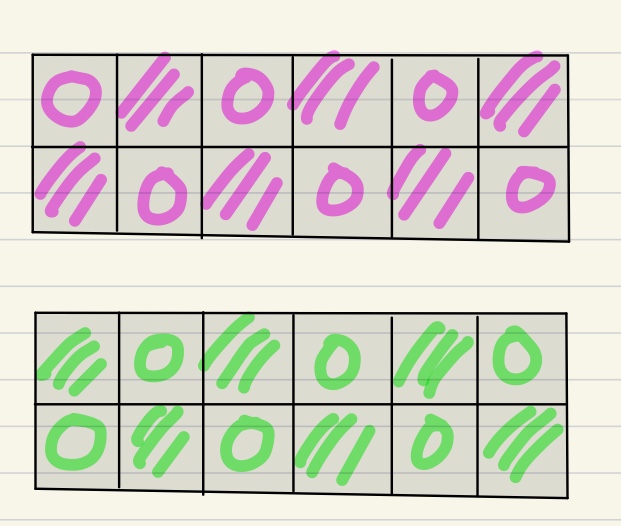
• 다음이 최대한 많이 스티커를 떼어낼 수 있는 경우의 수 두 가지이
  다.
• 스티커는 o, 변을 공유하여 사용할 수 없는 스티커는 빗금(//)표시하였다.

2. 스티커를 떼어낸 후 다음 스티커로 넘어갈 때 남은 빈 칸이 없어야한다.
   

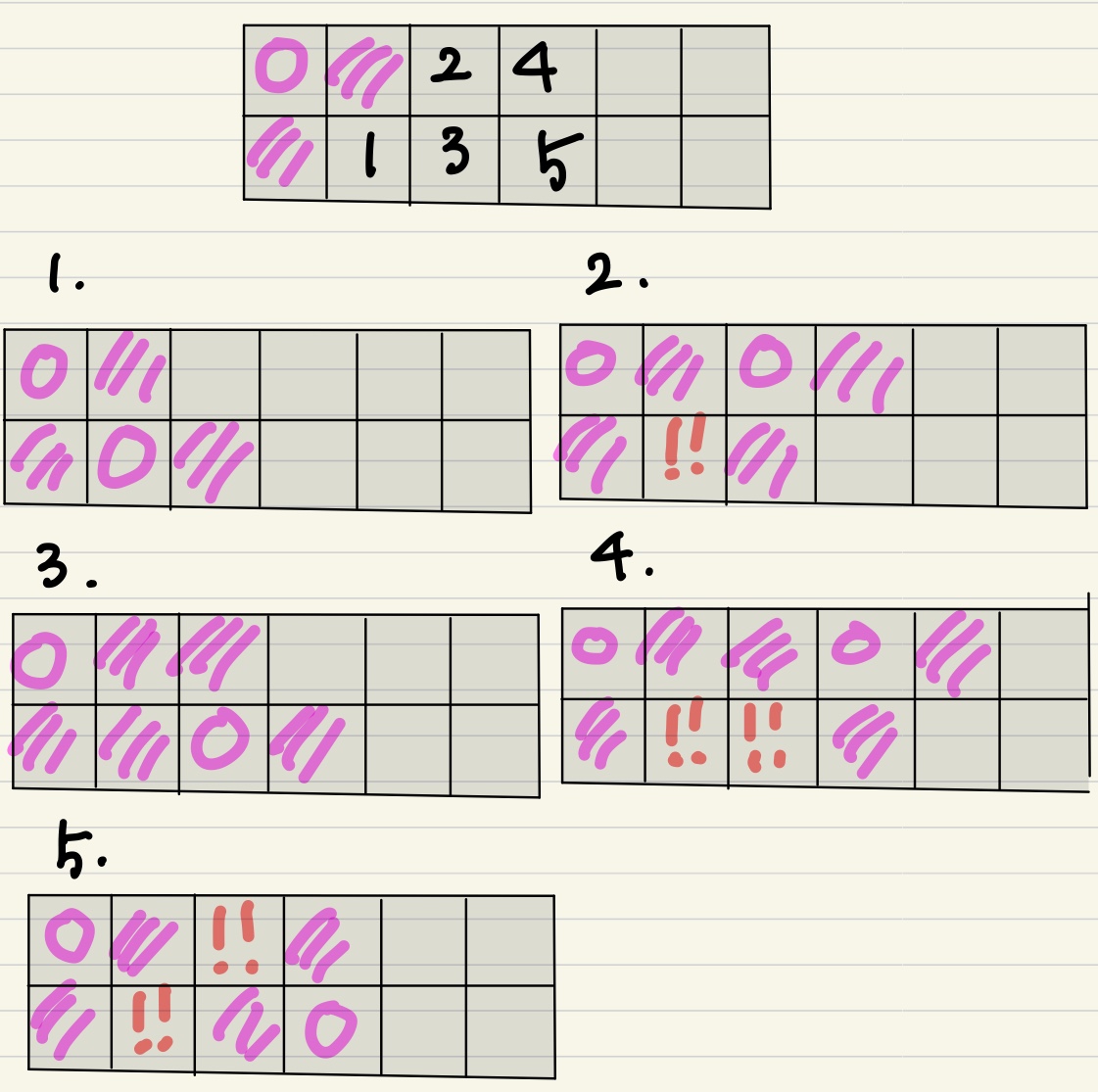
첫번째 [0,0]배열의 스티커를 뗀 경우
1, 2, 3, 4, 5 번 칸으로 이동이 가능한데
2, 4, 5 번 칸으로 이동할 경우 남는 칸(!!)이 생기기 때문에 최대값이 될 수 없다.

따라서 남는 칸이 생기지 않는 1번 또는 3번으로 이동하여야 최대값을 구할 수 있다. (1번칸으로 이동하는 경우가 1번의 최대한 많은 개수의 스티커를 떼는 경우와 같다.)

이것을 코드로 나타내기 위해서는 역으로 생각해야한다.
만약 지금 3번 스티커를 뗀다고 생각했을 때
그 이전 스티커는 [0][0]일 수도 있고, [0][1]일 수도 있다.
따라서 3번 스티커까지를 뗀 최대값은 3번 스티커의 값 + max([0][0], [0][1]) 이 될 것이다.

최종 풀이

import Foundation

let testCase = Int(readLine()!)!

for _ in 0..<testCase {
    
    let N = Int(readLine()!)!
    let numArray1 = readLine()!.split(separator: " ").map {Int(String($0))!}
    let numArray2 = readLine()!.split(separator: " ").map {Int(String($0))!}
    var dp = Array(repeating: Array(repeating: 0, count: N), count: 2)
    
    if N == 1 {
        print(max(numArray1[0], numArray2[0]))
    } else {
        dp[0][0] = numArray1[0]
        dp[1][0] = numArray2[0]
        dp[0][1] = dp[1][0] + numArray1[1]
        dp[1][1] = dp[0][0] + numArray2[1]
    
        for i in 2..<N {
            dp[0][i] = numArray1[i] + max(dp[1][i-1], dp[1][i-2])
            dp[1][i] = numArray2[i] + max(dp[0][i-1], dp[0][i-2])
        }
        print(max(dp[0][N-1], dp[1][N-1]))
    }
}

다음과 같이 풀 수 있다.