[Swift] 백준 11057 - 오르막 수

문제 링크

• N = 1일 때 : 10
• N = 2일 때 : 10 + 9 + 8 + ...+1 = 55
• N = 3일 때 : 55 + 45 + 36 + ...+ 1 = 220

자릿수와 해당 수로 시작하는 오르막 수의 개수를 가지는 이차원 배열 dp를 만든다.
예를 들어 자릿수(N)이 3이고 4로 시작하는 오르막 수 (444, 445, 467 등)의 개수 dp[3][4]에 들어간다.

따라서 길이가 N인 오르막 수의 개수는 dp[N][0]부터 dp[N][9]까지의 합이다.

최종 코드

import Foundation

let N = Int(readLine()!)!

var dp = Array(repeating: Array(repeating:0,count:10), count: 1001)
var sum = 0

for i in 0...9 {
    dp[1][i] = 1
}

if N > 1 {
    for i in 2...N {
        for j in 0...9 {
            for k in j...9 {
                dp[i][j] = (dp[i][j] + dp[i-1][k])%10007
             }
         }
     }
 }
 
for i in 0...9 {
    sum = (sum + dp[N][i])%10007
}
 
print(sum)
 

그러나 다른 분들의 풀이를 보고 훨씬 더 간편한 방법을 찾았다.

각 배열의 원소 값이 본인+앞 자리 값이고
이 배열의 원소들의 합을 구해야하는
문제이기 때문에

그러니까
N = 1일 때는
[1,1,1,1,1,1,1,1,1,1]배열의 원소들의 합이고,
N = 2 일 때는
[1,2,3,4,5,6,7,8,9,10] 배열의 원소들의 합이고
N = 3 일 때는
[1,3,6,10,15,21,28,36,45,55]의 원소들의 합이기 때문에

let N = Int(readLine()!)!

var dp = Array(repeating:1, count: 10)

for _ in 1..<N {
    for i 1...9 {
        dp[i] = (dp[i-1] + dp[i])%10007
    }
}

print(dp.reduce(0, {$0 + $1})%10007)

• 다음과 같이 간단하게 표현할 수도 있다.

- reduce

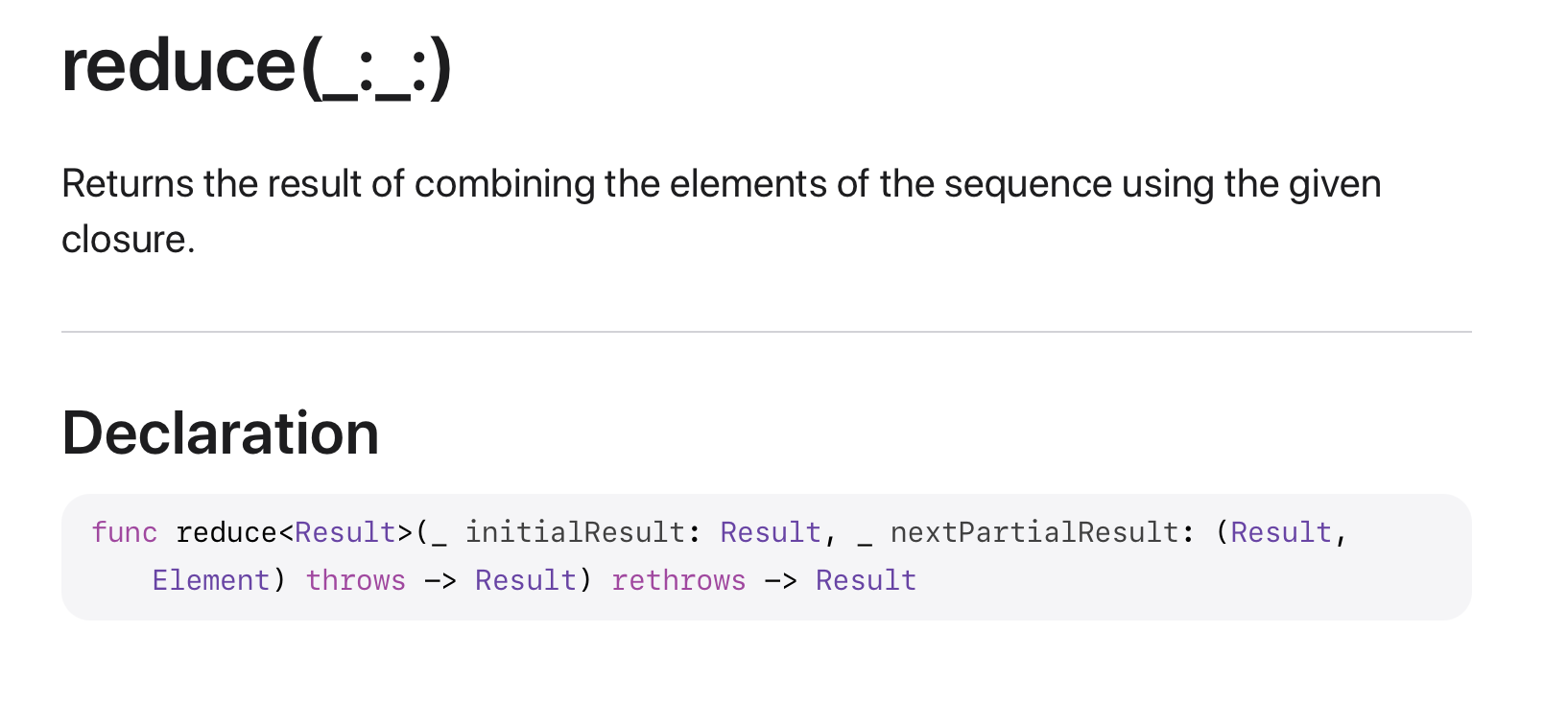
배열의 원소들의 합을 반환해주는 함수이다.

let numbers = [1, 2, 3, 4]
let numberSum = numbers.reduce(0, { x, y in
    x + y
})

• reduce(초기값, (결과,원소)) 이기 때문에
  • (0 + 1)
  • (1 + 2)
  • (3 + 3)
  • (6 + 4) 의 과정을 거쳐
  • => 10 을 반환한다.