[Python] 머신러닝 완벽 가이드 # 15. 로지스틱 회귀

✏️ # 15. 로지스틱 회귀

로지스틱 회귀(Logistic Regression)

• 로지스틱 회귀는 선형 회귀 방식을 분류에 적용한 알고리즘이다. 즉, 로지스틱 회귀는 분류에 사용된다.

• 로지스틱 회귀가 선형 회귀와 다른 점은 선형 함수의 회귀 최적선을 찾는 것이 아니라 시그모이드(𝜎) 함수의 최적선을
  찾고 이 시그모이드 함수의 반환 값을 확률로 간주해 확률에 따라 분류를 결정한다는 것이다.

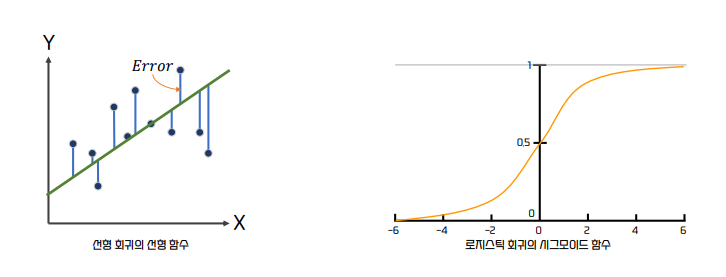
로지스틱 회귀 예측

• 로지스틱 회귀는 주로 이진 분류(0과 1)에 사용된다.

• 다중 분류에도 사용이 될 수 있다.

• 로지스틱 회귀에서 예측 값은 예측 확률을 의미하며 예측 값(예측 확률)이 0.5 이상이면 1로, 0.5 이하이면 0으로 예측한다.

• 로지스틱 회귀의 예측 확률은 시그모이드 함수의 출력값으로 계산된다.

• 단순 선형 회귀 𝑦 = 𝑤1𝑥 + 𝑤0가 있다고 할 때

• 로지스틱 회귀는 0과 1을 예측하기에 단순 회귀식에 적용할 수는 없다.
  하지만 Odds(성공확률 p)을 통해 선형 회귀식에 확률을 적용한다. 성공확률이 p이면 실패 확률은 1-p이다.

  𝑂𝑑𝑑𝑠(𝑝) = 𝑝/(1 − 𝑝)

• 하지만 확률 p의 범위가 0 ~ 1 사이이고, 선형 회귀의 반환값인 −∞ ~ + ∞값에 대응하기 위해서
  로그 변환을 수행하고 아래와 같이 선형 회귀를 적용한다. 이를 로짓 변환(Logit)이라고 한다.

  log(𝑂𝑑𝑑𝑠(𝑝)) = 𝑤1𝑥 + 𝑤0

• 해당 식을 데이터 값 x의 확률 p로 정리하면 다음과 같다.

  𝑝(𝑥) =1/1 + 𝑒-(𝑤1𝑥+𝑤0)

• 로지스틱 회귀는 학습을 통해서 시그모이드 함수의 𝑤를 최적화하여 예측하는 것이다

사이킷런 로지스틱 회귀

• 사이킷런은 로지스틱 회귀를 LogisticRegression 클래스로 구현

• LogisticRegression의 주요 하이퍼 파라미터로 penalty, C, solver가 있다.

  • penalty : 규제 유형 설정. ‘l2’, ‘l1’ 설정 가능

  • C : 규제 강도를 조절하는 𝛼의 역수. 즉 C=1/alpha. C가 작을 수록 규제 강도가 커짐

  • solver : 회귀 계수 최적화를 위한 다양한 최적화(Optimization) 방식

    • lbfgs : 사이킷런 버전 0.22 부터 solver의 기본 설정값. 메모리 공간을 절약할 수 있고 CPU 코어 수가 많다면 최적화를 병렬로 수행 가능

    • liblinear : 사이킷런 버전 0.21 까지 solver의 기본 설정값. 다차원이고 작은 데이터 세트에서 효과적으로 동작하지만 국소 최적화(Local Minimum)에 이슈가 있고, 병렬 최적화가 불가능

    • newtown-cg : 좀 더 정교한 최적화를 가능하게 하지만, 대용량의 데이터에서 속도가 많이 느려짐

    • sag : Stochastic Average Gradient로서 경사 하강법 기반의 최적화를 사용. 대용량의 데이터에서 빠르게 최적화 가능

    • saga : sag와 유사한 최적화 방식이며 L1 정규화를 가능하게 해준다

📌 참고 문헌

• 책

  • 📕 파이썬 머신러닝 완벽 가이드 / 권철민

• 참조 자료

  • 🔗 https://scikit-learn.org/stable/modules/linear_model.html

• 해당 챕터의 실습 및 예제 코드는 아래 링크의 Machine Learning 참조 해주시면 됩니다.

  • ✍️ DataSci-Notes