딥러닝에서의 Bayes rule (loss function)

선비Sunbei·2025년 3월 11일

Optimization

목록 보기

4/4

딥러닝 loss에 대해서 증명을 할 때 일반적으로 Bayes rule을 이용해서 증명을 한다.
하지만 나는 왜 딥러닝의 결과물은 input에 대해서 단일 값인데 어떻게 확률론 혹은 Bayes rule로 설명하는지 이해가 되지 않았다.
이에 대해서 이해한 부분을 작성하려고 한다.

Bayes rule

일단 Bayes rule에 대해서 정리하고 시작하고자 한다.
베이즈 정리는 다음과 같은 수식이다.

Pr(H|E) = \frac{Pr(E|H)Pr(H)}{Pr(E)}

Pr(X) : 특정 확률 분포(X)에 대한 확률
E : 증거(GT)에 대한 확률 분포
H : 가설(추측)에 대한 확률 분포

Pr(H|E) : 사후 확률(posterior probability)
Pr(E|H) : 우도(likelihood)
Pr(H) : 사전 확률(prior probability)
Pr(E) : 증거의 전체 확률(marginal likelihood)

Bayes rule에서 얘기하는 것은 간단하다.
기존의 가설에 대한 사전 확률(Pr(H))에 가설에 적합한 새로운 증거가 주어졌을 때 (likelihood를 통해) 갱신시켜서, 증거에 대한 가설의 확률을 구한다는 것이다.

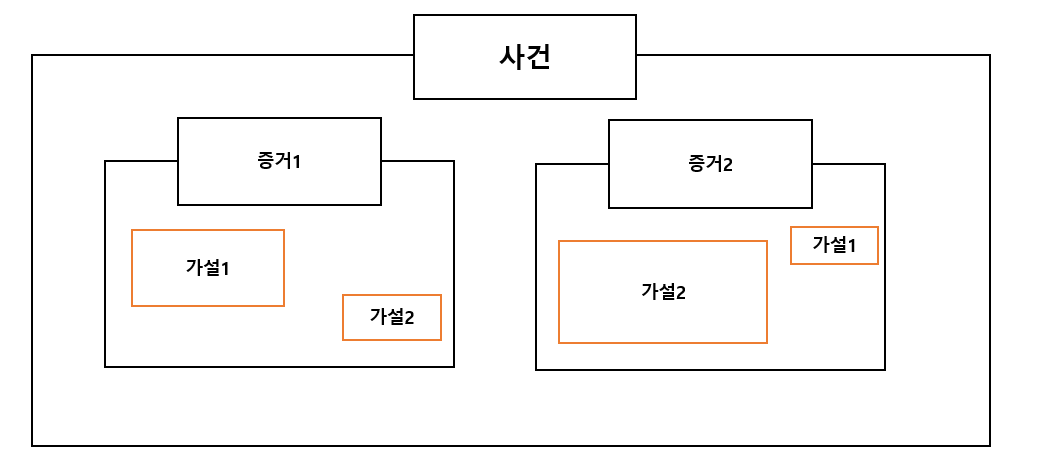
그림은 사후확률에 대한 것을 그린 것이다.
조금 풀어서 작성하면,
사후 확률은 어떤 사건에 대해서 여러 가설을 세울 수 있고, 우리가 얻은 증거에 대해서 어떤 가설이 더 적합한지 확률을 구하는 것이다.
증거가 특정 가설에 적합하다는 것을 likelihood를 통해서 업데이트 하는 것이 bayes rule이다.

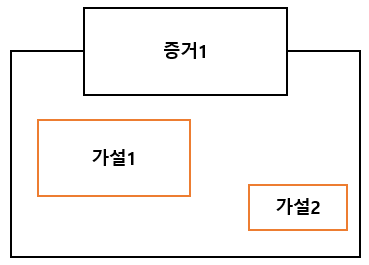
Pr(H|E) (사후확률)를 conditional probability로 생각하면 특정 증거에서 가설의 확률을 보겠다는 뜻이다.

Bayes rule in deep learning

딥러닝에서의 증거와 가설은 다음과 같이 매핑된다.

증거(E) : classification 혹은 regression에서의 label (GT)
가설(H) : 딥러닝의 output

가설은 우리가 추정하고 싶은 것을 의미하고, 우리는 딥러닝의 파라미터를 알고 싶기 때문에 딥러닝을 가설로 볼 수 있다.

이제부터는 증거와 가설이라는 말 대신 다른 기호로 바꿔서 사용하겠다.

y : 증거(E) : classification 혹은 regression에서의 label (GT)
$\phi$ : 가설(H) : 딥러닝의 output

근데 베이즈 룰에서 얘기하는 데이터는 확률 분포이다.
즉, $\phi$ 와 y 모두 확률 분포이다.

그런데 딥러닝의 output을 생각해보면 input에 매핑되는 output 단일 값이 나오는데 이게 어떻게 확률 분포이냐? 라는 질문이 나올 수 있다. 이는 추후 설명할 I.I.D. (independent and identically distributed로 인해서 발생하는 가정(assumption)이 있기 때문이다.
이는 나중에 설명할 것이므로, 결국 딥러닝의 output이 확률 분포이고, label(y) 또한 확률 분포라고 생각하고 넘어가면 된다.

Pr(\phi|y) = \frac{Pr(y|\phi)Pr(\phi)}{Pr(y)}

이제 다시 변경한 기호로 bayes rule을 작성하면 다음과 같다.

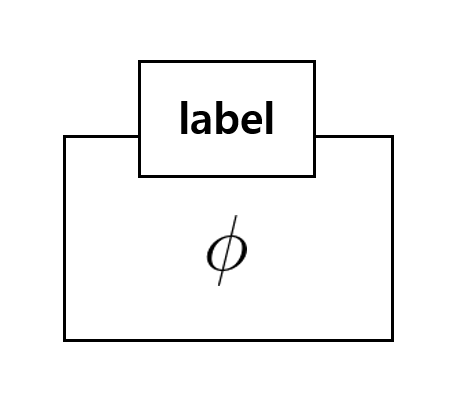
여기서 다시 사후확률을 conditional probability로 설명하면, 특정 label일 때의 특정 가설에 대한 확률을 구하는 것이다.
딥러닝 관점에서는, 딥러닝은 어떠한 확률 분포를 만들어내는데, 특정 label일 때 딥러닝이 만들어낸 확률 분포가 label에 대한 확률 분포와 얼마나 비슷한지 확률을 구하는 것이다.

MAP (Maximum A Posterior)

우리가 원하는 것은 딥러닝이 만들어낸 확률 분포가 label에 대한 확률 분포와 최대한 비슷한 것이다. 여기서 나오는 것이 MAP(Maximum A Posterior)이다.

수식으로 보면 다음과 같다.

\argmax_{\phi} Pr(\phi|y)

label은 고정적이기 때문에, 우리가 변경할 수 있는 파라미터는 $\phi$ 뿐이다.

input을 $x_i$ , input에 매칭되는 label을 $y_i$ , 딥러닝 네트워크의 파라미터를 $\theta$ 라고 하고, 딥러닝 네트워크를 NN(x, $\theta$ )라고 하자.
그럼 $\phi$ = NN(x, $\theta$ )이다.
input은 변경할 수 없으므로 사실상 위에서 말하는 수식은 다음과 같이도 변경할 수 있다.

\argmax_{\phi} Pr(\phi|y) = \argmax_{\theta} Pr(\phi = NN(x_i,\theta)|y = y_i)

이렇게 사후확률 최대화하게끔 딥러닝의 loss를 설계하면 된다.
하지만 아쉽게도 우리는 실제 세계의 $\phi$ 를 바로 찾을 수 없다.
(모수이기 때문에)

MLE(Maximum Likelihood Estimation)

따라서 bayes rule에 따라서 바꿔서 볼 것이다.

\argmax_{\phi} P(\phi|y) = \argmax_{\phi} \frac{P(y|\phi)P(\phi)}{P(y)}

여기서 생략할 수 있는 텀이 존재한다.
argmax이기 때문에 $\phi$ 와 관련없는 prior(P(y))를 없앨 수 있으며(상수이기 때문에), P( $\phi$ )는 뒤에 나올 I.I.D에 의해서 지울 수 있다.
(간략하게 말하면 모든 데이터의 분산이 동일하다는 가정으로 인해서, 어떤 데이터를 넣어도 분산이 같으므로 확률은 똑같이 나온다)

\argmax_{\phi} Pr(y|\phi)

즉, 우도를 최대화하게 하는 MLE(Maximum Likelihood Estimation) 문제로 변경된다.

우도를 사용함으로써 가질 수 있는 장점이 또한 존재한다.
우도가 가질 수 있는 값의 대수는 positive real number이다.
따라서 '확률의 합은 1이다.'라는 사후확률에 존재하는 제약 조건을 일부 벗어날 수 있게 된다.

MLE를 최대한으로 하면 우리는 좋은 성능의 딥러닝 네트워크를 만들 수 있을 것이다.
딥러닝에서 해당 수식을 사용하기 위해서 loss라는 cost function을 사용하고 있다.

이 cost function의 특징은 항상 positive real number여야 한다.
0에 가까울수록 좋고, 0에서 멀수록 좋지 않다. 라는 개념을 갖고 있다.

따라서 MLE를 조금 수정할 것이다.

I.I.D (independent and identically distributed)

MLE를 수정하기 전에 '딥러닝의 output이 확률 분포다.' 라는 것을 이야기 하기 위해서는 I.I.D (independent and identically distributed)라는 가정이 있다고 했다.
이를 얘기하고 MLE를 조금 수정해 보겠다.

I.I.D는 한국어로는 '독립 항등 분포'이다.
I.I.D는 2가지 가정을 얘기한다.

Independent(독립적)

각각의 데이터는 다른 것들과 상관없이 독립적으로 발생하여 다른 데이터나 변수에 영향을 미치지 않는다는 것을 얘기한다.

학습을 위한 input 데이터들을 x, 라벨들을 y라고 했다.
즉, 여러개의 데이터가 존재하는데 각 input 데이터와 라벨은 매칭되어있게 준비되었다고 하자.

mapping(x_i , y_i), \forall x_i \in x , \forall y_i \in y

그럼 MLE를 원칙대로 적으면 다음과 같다.

Pr(\phi_{x_0}, \phi_{x_1}, \phi_{x_2}, ... | y_0, y_1, y_2, ...)

하지만 독립적이라는가정으로 인해서 다음과 같이 표현할 수 있다.

Pr(\phi_{x_0}, \phi_{x_1}, \phi_{x_2}, ... | y_0, y_1, y_2, ...) = \prod_{i=0}^{N-1}Pr(\phi_i, y_i)

identically distribution

모든 데이터에 대해서 분산이 똑같다는 가정을 한다.
따라서 딥러닝의 output이 단일 값(이때 이 단일 값을 평균이라고 함)임에도 단일 값과, 동일한 분포를 가정하고 있기에 확률 분포를 만들 수 있게 된다. 여기서 동일한 분포라는 것은 임의의 상수로 설정할 수 있다는 것이다.

Maximum log-likelihood

다시 MLE로 돌아와서 우리는 MLE를 변형할 것이다.
가장 먼저 변형하는 것은 log를 씌울 것이다.
log는 단조 증가이기에 기존 '값의 차이가 존재한다'라는 사실은 그대로 유지하면서 scaling을 할 수 있다. 즉, argmax 에서는 곱해서 추가해줄 수 있게 된다.

\hat{\phi} = \argmax_{\phi} \prod_{i=0}^{N-1} Pr(y_i|\phi_i) \\ = \argmax_{\phi} (\log ( \prod_{i=0}^{N-1} Pr(y_i|\phi_i) )) \\ = \argmax_{\phi} (\sum_{i=0}^{N-1} \log Pr(y_i|\phi_i)) \\ = \argmax_{\theta} (\sum_{i=0}^{N-1} \log Pr(y_i|\phi_i = NN(x_i,\theta)))

이를 maximum log-likelihood라고 한다.
1번째 줄은 I.I.D에서의 independent로 표현한 것이며,
2번째 줄로의 변환은 log를 추가한 것이다.
3번째 줄로의 변환은 log의 성질로 product에서 summation으로 바꿀 수 있게 된다.
4번째 줄의 의미는 결국 최종적으로 네트워크의 파라미터인 $\theta$ 를 바꿔서 사후 확률을 최대화 하는 것이다.

Minimum negative log-likelihood

다음으로는 -를 붙여줘서 argmax를 argmin으로 바꿀 것이다.
이것은 cost function의 특징인 '0에 가까울 수록 좋고, 멀면 나쁘다.'라는 성질에 맞춰주기 위해서이다.

\hat{\phi} = \argmax_{\theta} (\sum_{i=0}^{N-1} \log Pr(y_i|\phi_i = NN(x_i,\theta)) ) \\ = \argmin_{\theta} -(\sum_{i=0}^{N-1} \log Pr(y_i|\phi_i = NN(x_i,\theta)))

그럼 최종적으로 Negative log-likelohood가 나오게 된다.

실제로 MSE를 간단하게 유도를 해보겠다.
MSE는 가우시안 분포를 가정한다.
따라서 $Pr(y_i|\phi_i)$ 를 다음과 같이 쓸 수 있다.

Pr(y_i|\phi_i) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp^{-\frac{(y_i- \mu_i)^2}{2\sigma^2}}

여기서 $\mu$ 는 딥러닝이 추론한 값이며, $\sigma$ 는 I.I.D에 의해서 원하는 값으로 설정할 수 있다.
해당 수식을 Negative log-likelihood에 넣으면 다음과 같이 정리할 수 있다.

\hat{\phi} = \argmin_{\theta} -(\sum_{i=0}^{N-1} \log Pr(y_i|\phi_i)) \\ = \argmin_{\theta} -\sum_{i=0}^{N-1}( \log(\frac{1}{\sqrt{2\pi\sigma^2}}) -\frac{(y_i- \mu_i)^2}{2\sigma^2} ) \\ = \argmin_{\theta} \sum_{i=0}^{N-1}(\frac{(y_i- \mu_i)^2}{2\sigma^2} - \log(\frac{1}{\sqrt{2\pi\sigma^2}})) \\ = \argmin_{\theta} \sum_{i=0}^{N-1}(\frac{(y_i- \mu_i)^2}{2\sigma^2}) \\ = \argmin_{\theta} \sum_{i=0}^{N-1}(y_i- \mu_i)^2

1번째 줄은 Negative log-likelihood이며,
2번째 줄은 $Pr(y_i|\phi_i)$ 에 가우시안 분포를 적용하고, log를 적용하여 정리한 것이다.
3번째 줄은 argmax를 argmin으로 바꾸면서 곱해준 -1을 분배법칙을 진행한 것이며
4번째 줄은 log 항이 $\phi$ 와 무관하기에 지워서 나온 것이다.
5번째 줄은 I.I.D의 가정인 분산은 똑같다. 에서 $\frac{1}{\sqrt{2}}$ 로 설정하여 없에준다.
최종적으로 MSE function이 나오게 된다.

그래서 해당 함수를 최소화하는 $y_i = \mu_i$ 로 되게끔 딥러닝 파라미터를 학습시키는 것이다.

지금까지 얘기한 것은 학습을 시킬 때 loss가 어떻게 설계되었느지이다.
이제 inference할 때는 어떻게 하는지 보겠다.

Inference

train된 model 파라미터를 $\hat{\theta}$ 라고 하겠다.
그럼 다음과 같이 확률 분포를 만들어내는 딥러닝 네트워크를 만들 수 있다.

\hat{\phi} = NN(x_j, \hat{\theta})

여기서 $x_j$ 는 train할 때 사용하지 않은 데이터 즉, 처음보는 데이터이고 이에 매칭되는 label은 알 수 없는 상태이다.
그리고 우리가 알고 싶은 것은 inference 시 나오는 학습된 라벨들에 가까운 label을 알아내는 것이다.
따라서 수식적으로 Maximum likelihood를 적으면 다음과 같다.

\hat{y} = \argmax_y Pr(y|\hat{\phi}= NN(x, \hat{\phi})) \\ = \argmax_y \frac{1}{\sqrt{2\pi\sigma^2}}\exp^{-\frac{(y - \hat{\mu_j})^2}{2\sigma^2}} \\ = \hat{\mu_j}

선비Sunbei

이전 포스트