다익스트라 알고리즘이란?

다익스트라(Dijkstra)는 한 정점(시작 정점)에서 부터 모든 정점까지의 최단 거리를 각각 구하는 알고리즘이다.

이 때 그래프는 음의 간선을 포함하지 않아야 한다.

다익스트라 알고리즘은 다이나믹 프로그래밍, 그리디 알고리즘 기법을 사용한 알고리즘이라고 볼 수 있다.
그 이유는 다익스트라의 기본적인 메커니즘을 보면 알 수 있다.

각 정점을 노드, 간선간의 거리를 비용이라 하자.
방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택한다. -> 그리디 알고리즘
해당 노드로부터 갈 수 있는 노드들의 비용을 갱신한다. -> 다이나믹 프로그래밍

기본적인 매커니즘은 알아봤으므로 이제 다익스트라가 어떻게 동작하는지 본격적으로 알아보도록 하자.

다익스트라 동작 방식

정점이 6개인 그래프에서 시작 정점을 A로 설정 하고 다익스트라를 적용해보자.

각 데이터의 의미는 다음과 같다.

S : 방문한 노드들의 집합
Q : 방문하지 않은 노드들의 집합
d[N] : A -> N까지 계산된 최단 거리
INF : 확인되지 않은 거리 = 무한

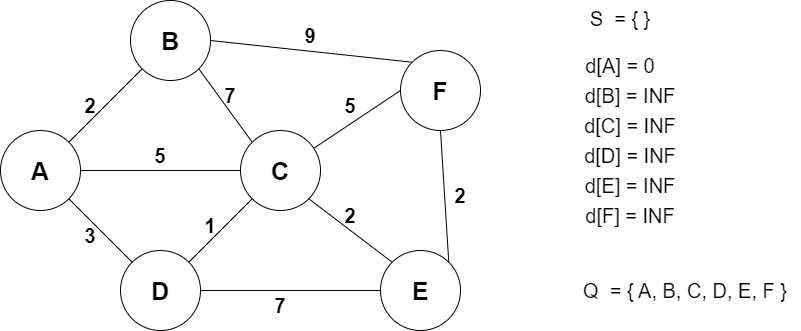
아직 방문한 노드가 없기 때문에 S는 공집합이고 Q는 모든 노드들의 집합이다.
출발지인 A에서 A까지의 거리는 0이므로 0으로 설정, 나머지 노드들까지의 거리는 확인되지 않았으므로 INF

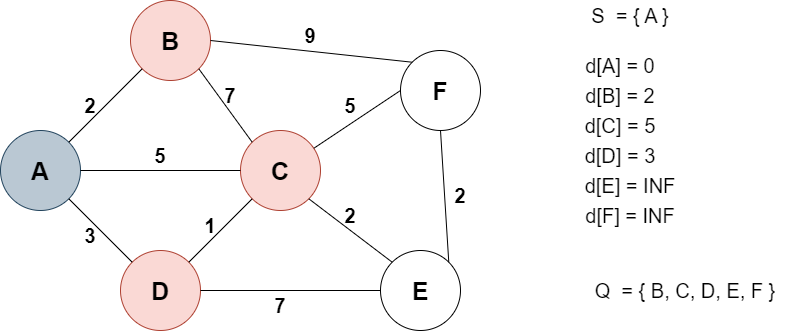
A에서 방문할 수 있는 노드는 B, C, D다.
A에서 해당 노드까지 가는 거리를 각각 기존의 거리값과 비교해 최솟값으로 업데이트 한다.
예를 들어 A에서 B까지의 거리는 2이므로 d[B]는 기존의 INF와 2중 작은 값인 2로 업데이트 된다.
인접 노드까지의 거리를 모두 업데이트 한 A는 더이상 방문할 필요가 없으므로 Q에서 제외하고 S에 추가한다.

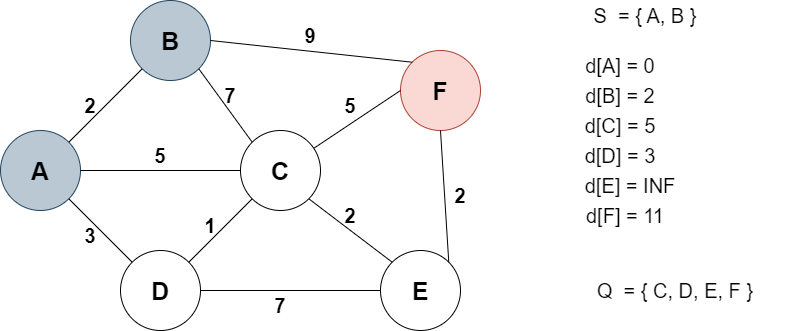
갱신한 테이블 중 가장 거리값이 작은 노드인 B를 다음 노드로 선택한다.
B에서 방문할 수 있는 노드는 C와 F다.
C로 갈 수 있는 경로(A->B->C)가 존재하므로 C까지의 거리값의 기존의 거리값과 비교한다.
기존의 거리값은 5, A->B->C는 9이므로 업데이트 하지 않는다.
F로 가는 거리값이 11, 기존의 거리값이 INF이므로 최소값인 11로 업데이트 한다.
B도 마찬가지로 인접한 노드까지의 거리를 모두 업데이트했으므로 Q에서 제외하고 S에 추가한다.

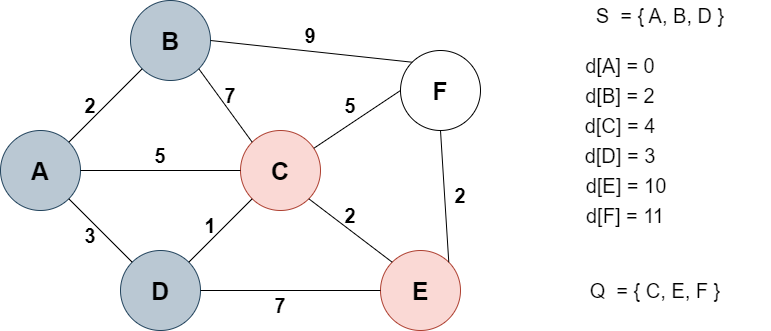
그 다음으로 거리값이 작았던 D를 다음 노드로 선택한다.
C로 가는 경로(A->D->C)의 거리값이 4로 기존의 5보다 작으므로 4로 업데이트 해준다.
E로 가는 거리값도 10으로 업데이트 해준다.
Q에서 제외, S에 추가한다.

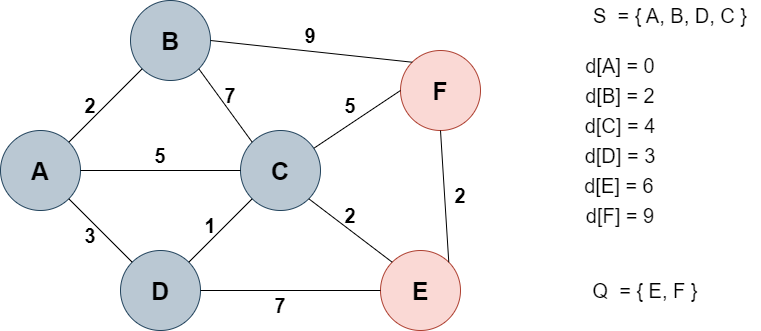
C노드를 선택했을 때 거리값 업데이트
d[E] : 10 -> 6
d[F] : 11 -> 9

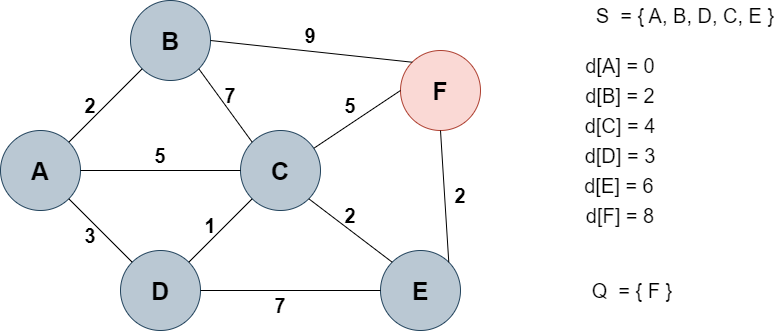
E노드를 선택했을 때 거리값 업데이트
d[F] : 9 -> 8

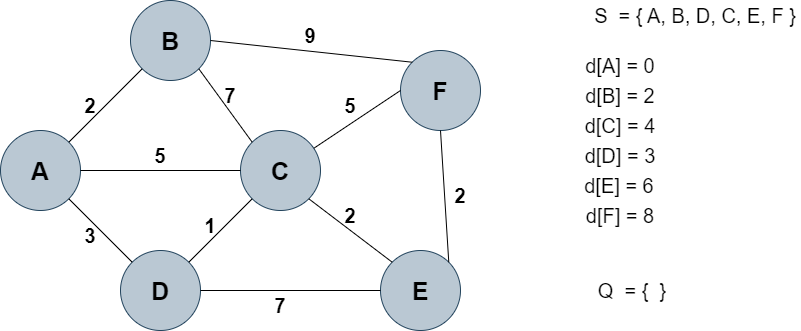
위 과정이 반복되어 Q가 공집합이 되면(= 모든 노드에 대해 거리값 계산 완료) d를 통해 각 노드까지의 최단 거리를 결정한다.

구현 방법

다익스트라 알고리즘은 크게 두가지 방식으로 구현할 수 있다.
의사코드를 보며 각 방식의 동작 원리를 이해해보자.

선형 탐색

def dijkstra_linear(graph, start):
    n = len(graph)
    INF = float('inf')
    distance = [INF] * n
    visited = [False] * n
    distance[start] = 0

    for _ in range(n):
        # 방문하지 않은 노드 중 최단 거리 노드 찾기 (O(N))
        min_dist = INF
        min_node = -1
        for i in range(n):
            if not visited[i] and distance[i] < min_dist:
                min_dist = distance[i]
                min_node = i

        # 선택한 노드 방문 처리
        if min_node == -1:
            break
        visited[min_node] = True

        # 인접한 노드의 거리 갱신
        for neighbor, cost in graph[min_node]:
            if distance[min_node] + cost < distance[neighbor]:
                distance[neighbor] = distance[min_node] + cost

    return distance

1. 모든 노드의 최단 거리 값을 무한대로 초기화
2. 시작 노드의 최단 거리 값을 0으로 설정
3. 방문하지 않은 노드 중 최단 거리 값이 가장 작은 노드를 선택
4. 선택한 노드를 방문 처리하고, 인접한 노드들의 최단 거리를 갱신 (기존 거리보다 짧은 경로를 발견하면 업데이트)
5. 모든 노드를 처리할 때까지 반복

구현이 간단하고 이해하기 쉽다는 장점이 있지만,
각 노드마다 방문하지 않은 노드 중 최솟값을 찾아야 하므로 시간복잡도가 $O(N^2)$다.

우선순위 큐

import heapq

def dijkstra_heap(graph, start):
    n = len(graph)
    INF = float('inf')
    distance = [INF] * n
    pq = []  # 우선순위 큐 (min-heap)
    
    # 시작 노드 초기화
    heapq.heappush(pq, (0, start))  # (거리, 노드)
    distance[start] = 0

    while pq:
        dist, node = heapq.heappop(pq)  # 현재 최단 거리 노드 꺼내기
        
        if distance[node] < dist:
            continue  # 이미 처리된 노드이면 무시
        
        for neighbor, cost in graph[node]:
            new_dist = dist + cost
            if new_dist < distance[neighbor]:
                distance[neighbor] = new_dist
                heapq.heappush(pq, (new_dist, neighbor))

    return distance

1. 모든 노드의 최단 거리 값을 무한대로 초기화
2. 시작 노드의 최단 거리 값을 0으로 설정하고, (0, 시작 노드)를 우선순위 큐에 삽입
3. 우선순위 큐에서 최단 거리 노드를 꺼내 방문 처리
4. 해당 노드의 인접 노드들을 탐색하며 최단 거리 갱신 (기존 거리보다 짧은 경로를 발견하면 우선순위 큐에 삽입)
5. 큐가 빌 때까지 반복

노드의 개수가 V, 간선의 개수가 E일 때 $O(logV)$의 연산으로 최단 거리 노드를 선택할 수 있으므로 시간복잡도가 $O(ElogV)$다.

노드의 개수가 많아지면 탐색 시간이 오래 걸리는 선형 탐색을 개선하기 위해 도입된 방법이다.
따라서 대부분의 경우 우선순위 큐 방식을 사용하는 것을 권장한다.

References
[필수 알고리즘] 다익스트라 알고리즘(Dijkstra Algorithm) 이해