[알고리즘] - 백준 11057번 : 오르막수(JAVA)

🎯 문제

문제 풀러가기

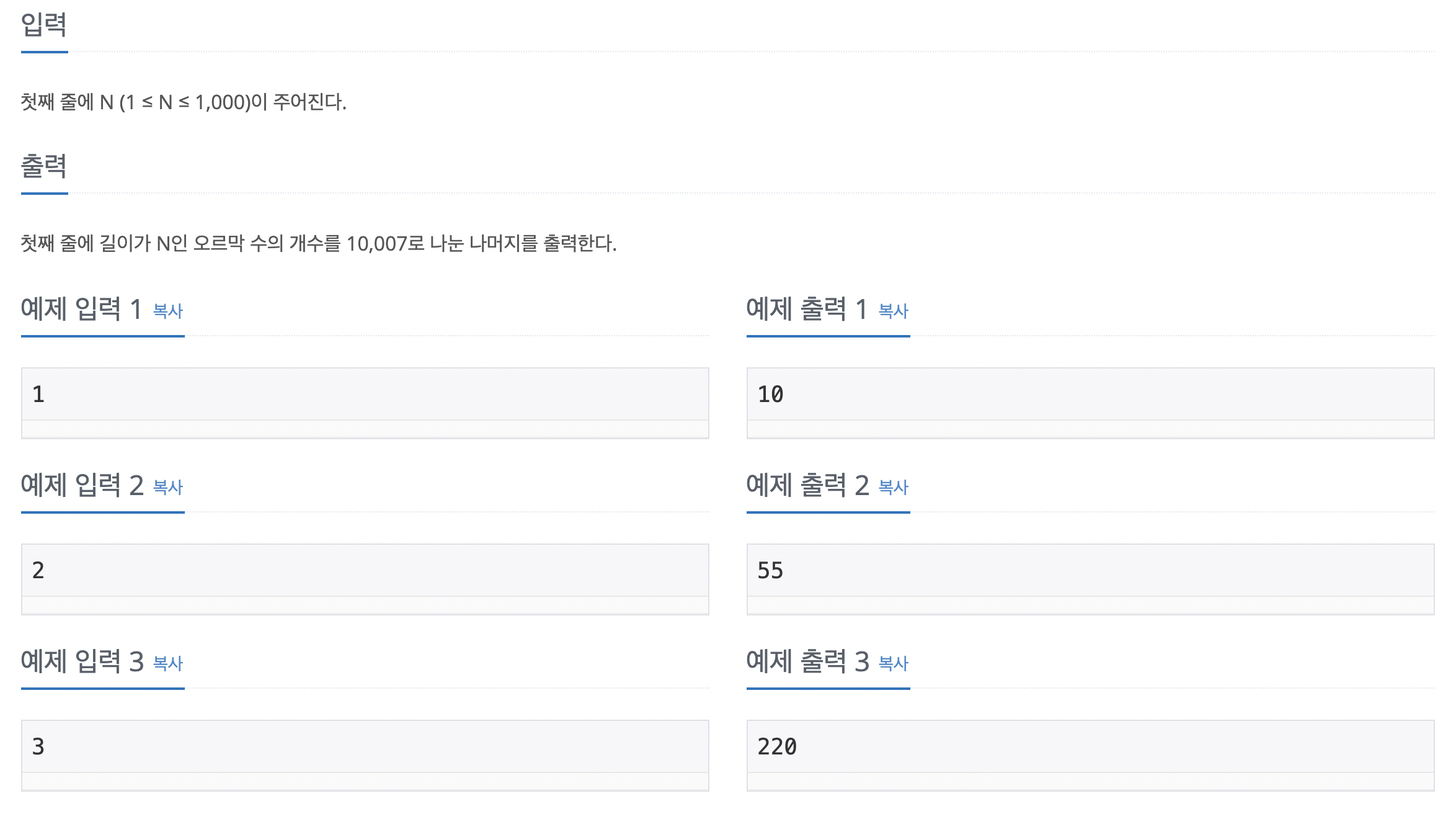
🎯 입력,출력

🚀 풀이방법

동적 계획법을 적용할 배열만 잘 생각 해 내면 쉽게(?) 풀릴 수 있는 문제 였습니다.
저는 배열을 이차원 배열로 생각을 하였으며
dp[자릿수][값] 이런 식으로 구성하였습니다.
이 말이 무엇이냐고 하면!

ex) dp[2][5]인 경우를 봅시다.
자릿 수가 2자리 수일 때 마지막 값이 5인 경우라고 생각하시면 됩니다.
즉, 여기서 오르막 수를 구해보자고 한다면 "15, 25, 35, 45, 55" 가 되겠죠..
그렇다면 dp[2][5]=dp[1][1]+dp[1][2]+dp[1][3]+dp[1][4]+dp[1][5] 이런 식으로 나올 것입니다.
이 점에 유의하여 문제를 쭉쭉 풀면 됩니다..
(자릿 수가 1인 경우는 배열을 1로 초기화 해 놓으시면 됩니다! 👍)

🚀 CODE

import java.util.Scanner;

public class Main {

    static int n;
    static int[][] dp;

    public static int dfs(int digit,int value){

        if(digit==1)
            return dp[digit][value];

        if(dp[digit][value]==0) {
            for (int i = 0; i < 10; i++) {
                if (value >= i) {
                    dp[digit][value]+=dfs(digit - 1, i);
                }
            }
        }

        return dp[digit][value]%10007;
    }

    public static void main(String[] args) throws Exception{
        Scanner scanner=new Scanner(System.in);
        n=scanner.nextInt();

        dp=new int[n+1][10];

        for(int i=0;i<10;i++){
            dp[1][i]=1;
        }
        int res=0;

        for(int i=0;i<10;i++){
            res+=dfs(n,i);
        }

        if(n==1){
            System.out.println(10);
        }else{
        System.out.println(res%10007);}

    }
}

👏 정답

PS. 괜하게 for문으로 풀면 시간도 빠르고 빠르게 답을 도출 해 낼 수 있는데.... 재귀로 풀어서 시간이 이 모냥 났습니당 ㅠ

😍 이상으로 포스팅을 마치겠습니다. 감사합니다 :)