[알고리즘] - 백준 13398번 : 연속합 2(JAVA)

🎯 문제

문제 풀러가기

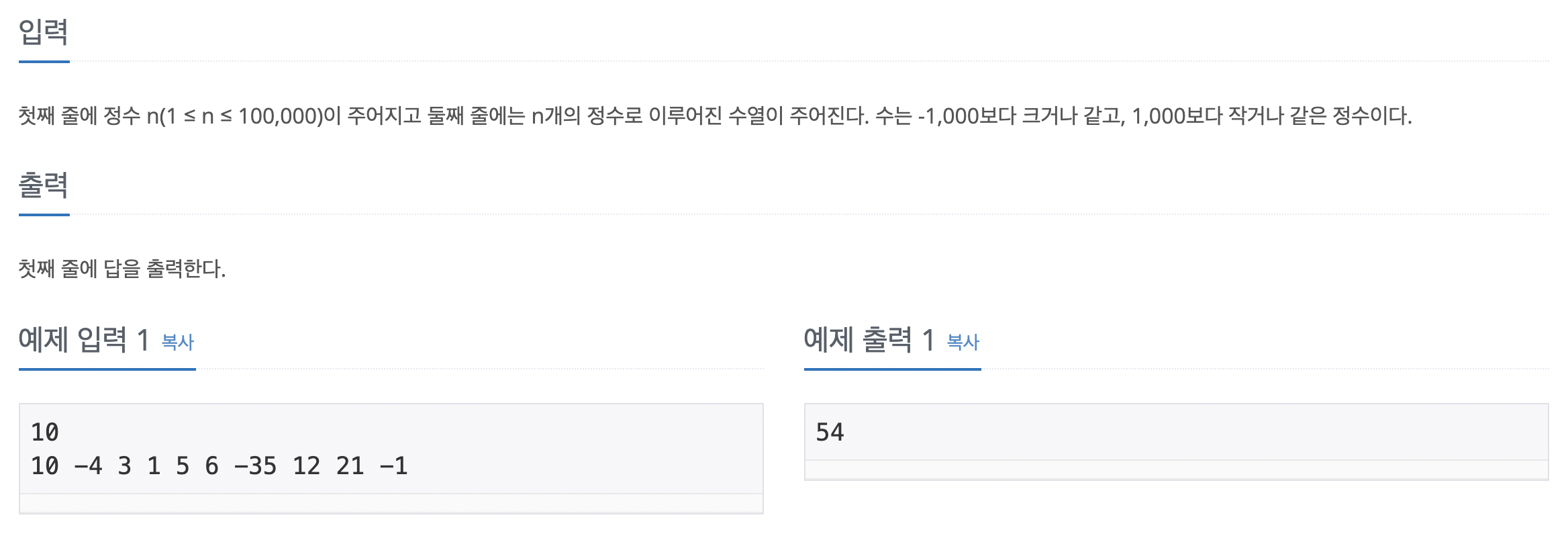
🎯 입력, 출력

🚀 풀이 방법

처음 문제를 풀 때 다양한 풀이 방법이 존재하는 것 같았습니다.
저의 문제 해결 전략은
연속합의 최대 값을 저장해놓을 일차원 배열을 두 개를 만들었습니다.

하나는 왼쪽에서 오른쪽으로의 합

• dp[n]=max(dp[n-1]+arr[n],dp[n])

나머지 하나는 오른쪽에서 왼쪽으로의 합

• dp[n]=max(dp[n+1]+arr[n],dp[n])

이렇게 구한 만든 이유를 봅시다 🙋‍♀️

문제를 보시면 입력이
10 -4 3 1 5 6 -35 12 21 -1
이런 식으로 존재 합니다..

숫자를 하나 제외 할 수 있다면
만약 저기서 6을 제외 해 본다고 합시다.

그러면 연속합의 값은 6을 제외 하고

왼쪽에서 오른쪽으로의 합
10 -4 3 1 5

오른쪽에서 왼쪽으로의 합
-35 12 21 -1

이 둘의 합을 구하면 되겠죠!!

정리하자면, 현재 값을 기준으로 좌측에서의 연속합+우측에서의 연속합을 구하면 되는 것 입니다!

이제는, 숫자를 제외 시킬 때 어느 방식으로 최대값을 구해야하는지를 알았기 때문에
값을 비교하며 최대 값을 갱신해 나가기 만 하면 됩니다!

🚀 CODE

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {

    static int n;
    static int arr[];
    static int[] dpL;
    static int[] dpR;


    private static int dfsL(int x){
        if(x==1)
            return dpL[1]=arr[1];
        if(dpL[x]>Integer.MIN_VALUE)
            return dpL[x];

        dpL[x]=Math.max(dfsL(x-1)+arr[x],arr[x]);

        return dpL[x];
    }

    private int static dfsR(int x){
        if(x==n)
            return dpR[n]=arr[n];
        if(dpR[x]>Integer.MIN_VALUE)
            return dpR[x];


        dpR[x]=Math.max(dfsR(x+1)+arr[x],arr[x]);

        return dpR[x];
    }


    public static void main(String[] args) throws Exception{
        BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st=new StringTokenizer(br.readLine());

        n=Integer.parseInt(st.nextToken());
        st=new StringTokenizer(br.readLine()," ");

        arr=new int[n+1];
        for(int i=1;i<=n;i++){
            arr[i]=Integer.parseInt(st.nextToken());
        }
        dpL=new int[n+1];
        dpR=new int[n+1];
        Arrays.fill(dpL,Integer.MIN_VALUE);
        Arrays.fill(dpR,Integer.MIN_VALUE);


        dfsL(n);
        int res= Arrays.stream(dpL).max().getAsInt();

        dfsR(1);

        for(int i=2;i<n;i++){
            res=Math.max(res,dpL[i-1]+dpR[i+1]);
        }
        

        System.out.println(res);
    }
}

👏 정답

😍 이상으로 포스팅을 마치겠습니다. 감사합니다 :)