educative - kotlin - 13

Programming Recursion and Memoization

재귀(recursion)을 활용하면 분할정복 문제를 해결할 수 있다.
퀵정렬 예시

fun sort(numbers: List<Int>): List<Int> =
  if (numbers.isEmpty())
    numbers
  else {
    val pivot = numbers.first()
    val tail = numbers.drop(1)
    val lessOrEqual = tail.filter { e -> e <= pivot }
    val larger = tail.filter { e -> e > pivot }

    sort(lessOrEqual) + pivot + sort(larger)
  }

println(sort(listOf(12, 5, 15, 12, 8, 19))) //[5, 8, 12, 12, 15, 19]

코틀린은 재귀함수를 지원하지만 해당 함수에 해단 return type을 반드시 명시해줘야 한다(타입 추론 불가)

Recursive vs iterative

재귀를 사용하려면 어느정도의 진입장벽은 있지만 한번 공부하면 유용하게 사용할 수 있다.

import java.math.BigInteger

fun factorialRec(n: Int): BigInteger =
  if (n <= 0) 1.toBigInteger() else n.toBigInteger() * factorialRec(n - 1)
    
println(factorialRec(5)) //120

위 factorialRec() 함수는 인자가 0이하로 들어오면 1을 반환한다. 인자가 0보다 크면 input과 자기자신을 재귀호출하는 값을 반환한다.

만약 재귀함수를 사용하지 않고 일반 interative한 함수를 짠다면 다음과 같다.

fun factorialIterative(n: Int) =
  (1..n).fold(BigInteger("1")) { product, e -> product * e.toBigInteger()}

fold() 함수는 앞서 정리했던 reduce()함수와 비슷하다. reduce()와는 초기 값과 람다 즉, 2개의 인자를 받는다는 점이 다르다. 위 예시에서 가독성은 재귀를 활용한 방법이 좀 더 좋은것 같다.

Drawback of recursion

재귀가 일반적인 접근법이랑 다른점은 메모리 사용량이 많아 스택을 키운다는 것이다, 따라서 계산 스택이 위험레벨에 도달하면 프로그램이 터질 수 있다. 예를들어 위에서 작성한 함수에 인자를 50000으로 넘겨줬을 때

iterative한 방법을 사용하면 별 문제가 없지만

println(factorialIterative(50000))

재귀를 사용했을때 StackOverflowError를 발생시킬 수 있다.

println(factorialRec(50000))

실행결과

java.lang.StackOverflowError
        at java.base/java.math.BigInteger.valueOf(BigInteger.java:1182) 
        at Largerecursive.factorialRec(largerecursive.kts:4)

Tail Call Optimization (꼬리 호출 최적화)

Tail Call이란 함수가 제일 마지막에 하는 일이 자기 자신을 호출하는 것이다. 코틀린에서 함수 앞에 tailrec이라는 키워드를 사용하면 코틀린이 마지막에 꼬리호출을 제거해준다.

tailrec fun factorialRec(n: Int): BigInteger =
  if (n <= 0) 1.toBigInteger() else n.toBigInteger() * factorialRec(n - 1)

함수 안에 n.toBigInteger() * factorialRec(n - 1)에서 factorialRec 함수가 가장 마지막에서 호출된다고 생각하겠지만, function call이 반환되기 전에 곱셈 연산부터 수행된다. 따라서 factorialRec()에 대한 호출이 끝날때 까지 기다리게 되는데 여기서 스택에 무리를 주게 된다.

따라서 다음과 같이 코드를 살짝 수정하면 50000을 인자로 넘겨줘도 잘 동작한다.

import java.math.BigInteger

tailrec fun factorial(n: Int, 
  result: BigInteger = 1.toBigInteger()): BigInteger =
    if (n <= 0) result else factorial(n - 1, result * n.toBigInteger())

println(factorial(5)) //120

println(factorial(50000)) //No worries

좀 더 내부적으로 확인해보기 위해 Factorial 객체를 만들고 재귀호출 방식의 함수와 꼬리 재귀 호출방식의 함수를 만들어보자.

import java.math.BigInteger

object Factorial {
  fun factorialRec(n: Int): BigInteger =
    if (n <= 0) 1.toBigInteger() else n.toBigInteger() * factorialRec(n - 1)

  tailrec fun factorial(n: Int, 
    result: BigInteger = 1.toBigInteger()): BigInteger =
      if (n <= 0) result else factorial(n - 1, result * n.toBigInteger())
}

코드를 컴파일하고 바이트 코드를 살펴보자

kotlinc-jvm Factorial.kt
javap -c -p Factorial.class

Compiled from "Factorial.kt" public final class Factorial {
public final java.math.BigInteger factorialRec(int); Code:
...
      38: invokevirtual #23
                 // Method factorialRec:(I)Ljava/math/BigInteger;
...
44: invokevirtual #27
// Method java/math/BigInteger.multiply:(...)
47: dup
48: ldc
#29 // String this.multiply(other)
...
public final java.math.BigInteger factorial(int, java.math.BigInteger); Code:
...
       7: ifgt          14
      10: aload_2
      11: goto          76
...
56: invokevirtual #27
// Method java/math/BigInteger.multiply:(...) ...
      73: goto          0
      76: areturn

factorialRec 의 바이트코드를 확인해보면 invokevirtual이 재귀적으로 fatorialRec()을 호출하고 multiply()를 호출한다.

factorial()의 바이트코드를 확인하면 invokevirtual 재귀 호출 없이 ifgt와 goto를 호출해 함수내에서 이동을 하고 있다. 재귀 호출의 과정이 iterative하고 돌고 있다는 증거다.

Memoization

메모이제이션 (Memoization)은 연속해서 사용되는 연산 값을 함수 레벨에서 캐싱하는것 을 지칭하기 위해 사용하는 단어이다. 피보나치 수열에서 하위 계산값에 대한 메모이제이션을 사용하는 여부에 따라 시간복잡도가 천차만별로 달라지는 예시가 있다.

Repetitive computation

위에서 예시로 든 피보나치에서 메모이제이션을 사용하지 않는다면?

import kotlin.system.measureTimeMillis
  
fun fib(n: Int) : Long = when (n) {
  0, 1 -> 1L
  else -> fib(n - 1) + fib(n - 2)  
}

println(measureTimeMillis { fib(40) }) //About 3 millisconds
println(measureTimeMillis { fib(45) }) //More than 4 seconds

피보나치에서 f(n)에 대한 값을 구하려면 f(n-1), f(n-2)에 대한 연산결과가 필요하다. 따라서 n의 값이 증가할수록 하위 계산값들이 필요하기 때문에 연산시간은 기하급수적으로 증가한다.

예시로 f(40)의 실행시간은 0.003초이지만 f(45)를 돌려볼 경우 실행시간이 4초로 늘어난다. 그렇다면 f(100)은 안해볼련다.

문제를 해결하기 위해 메모이제이션을 확장해서 사용해보자. memoize() 함수를 사용해준다.

fun <T, R> ((T) -> R).memoize(): ((T) -> R) {
  val original = this
  val cache = mutableMapOf<T, R>()

  return { n: T -> cache.getOrPut(n) { original(n) } }
}

원래 함수는 this 키워드를 사용해 original이라는 변수에 담고, 빈 값의 cache를 정의해준다. 마지막으로 T를 인자로 받고 R 타입을 반환하는 람다 표현식을 반환한다. 여기서 우리는 캐시를 확인해 값이 있으면 연산과정을 생략하고 저장된 값을 반환한다. 반대로 캐시안에 값이 없으면 해당 연산을 수행하고 값을 저장한다.

이제 피보나치 수열에서 메모이제이션을 구현해보자

lateinit var fib: (Int) -> Long

fib = { n: Int -> 
  when (n) {
    0, 1 -> 1L
    else -> fib(n - 1) + fib(n - 2)
  }
}.memoize()

맨 윗줄에서 lateinit 키워드를 사용하면 nullable하지 않은 프로퍼티 초기화를 미룰 수 있다. 이를 늦은 초기화라고 부른다.

여태까지 구현한걸 다 조합해서 실행시간을 비교해보자

import kotlin.system.measureTimeMillis

fun <T, R> ((T) -> R).memoize(): ((T) -> R) {
  val original = this
  val cache = mutableMapOf<T, R>()

  return { n: T -> cache.getOrPut(n) { original(n) } }
}

lateinit var fib: (Int) -> Long

fib = { n: Int -> 
  when (n) {
    0, 1 -> 1L
    else -> fib(n - 1) + fib(n - 2)
  }
}.memoize()

println(measureTimeMillis { fib(40) })
println(measureTimeMillis { fib(45) })
println(measureTimeMillis { fib(500) })

실행결과

0 
0 
1

깔끔하다.

memoize() 함수는 1개이상의 매개변수를 가진 모든 함수들에 대해서 사용할 수 있다. 람다 표현식을 memoization 버전으로 바꿀 수 있고 간결하다는 장점이 있다. 하지만 var fib를 위에서 정의해주고 다시 람다식을 할당하면 compliation error가 발생할 수 있다는 단점이 있다. 또한 fib가 var이라는 점이 찝찝하다.

Memoization as delegate

import kotlin.system.measureTimeMillis
import kotlin.reflect.*

class Memoize<T, R>(val func: (T) -> R) {
  val cache = mutableMapOf<T, R>()
  
  operator fun getValue(thisRef: Any?, property: KProperty<*>) = { n: T -> 
    cache.getOrPut(n) { func(n) } }
}

val fib: (Int) -> Long by Memoize {n: Int ->
  when (n) {
    0, 1 -> 1L
    else -> fib(n - 1) + fib(n - 2)
  }
}

println(measureTimeMillis { fib(40) })
println(measureTimeMillis { fib(45) })
println(measureTimeMillis { fib(500) })

앞서 달라진 점은 fib를 val로 선언했다는 점과 getValue()를 사용해 호출하는 함수를 사용해 캐싱을 해준다는 점이 있다. 조금 더 간결해졌다.

Dynamic programming

Dynamic Programming (동적 프로그래밍)은 재귀의 효율성을 극대화시키기 위해 메모이제이션을 사용하는 알고리즘 기법이다. 반복적인 재귀호출을 줄여 연산의 부담을 줄여준다.

앞서 사용했던 메모이제이션 위임 기법을 잘 알려진 DP 문제에 대입해보자.

유명한 막대 자리그(rod cutting) 문제이다

막대 자르기 문제는 다음과 같습니다.

길이가 n인 막대와 i = 1,2,3,...,n에 대한 가격 p_i의 표가 주어지면 해당 막대를 잘라서 판매했을떄 얻을 수 있는 최대수익 r_n을 결정하는 것 입니다. 길이가 n인 막대의 가격 p_n이 충분히 비싸면 최적해는 자르지 않은 것일 수도 있습니다.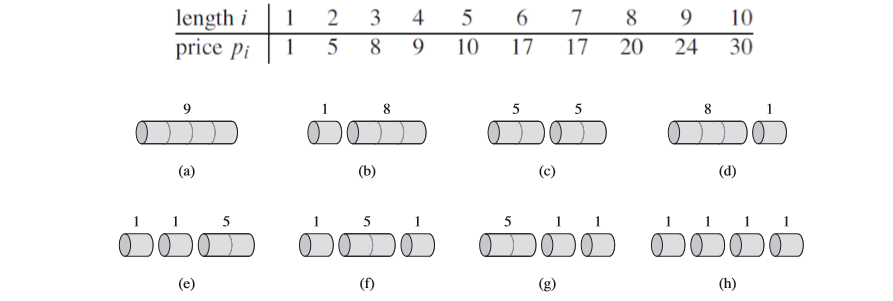

Sudo Code 풀이

maxPrice(length) =
  max {
                maxPrice(1) + maxPrice(length - 1), 
                maxPrice(2) + maxPrice(length - 2), 
                ...,
                maxPrice(length - 1) + maxPrice(1), price[length]
}

메모이제이션을 적용한 문제풀이

val prices = mapOf(1 to 2, 2 to 4, 3 to 6, 4 to 7, 5 to 10, 6 to 17, 7 to 17)

val maxPrice: (Int) -> Int by Memoize { length: Int ->
  val priceAtLength = prices.getOrDefault(length, 0)
  
  (1 until length).fold(priceAtLength) { max, cutLength ->
    val cutPrice =  maxPrice(cutLength) + maxPrice(length - cutLength)
    
    Math.max(cutPrice, max)
  }
}

for (i in 1..7) {
  println("For length $i max price is ${maxPrice(i)}")
}

실행결과

For length 1 max price is 2
For length 2 max price is 4
For length 3 max price is 6
For length 4 max price is 8
For length 5 max price is 10
For length 6 max price is 17
For length 7 max price is 19