백준 1629번 곱셈

분할정복 3step

1.divide

 기존 문제를 작은 부분문제들로 나눔
 ( break the problem into subproblems: smaller instances )
 
 base case(바로 답을 알 수 있는 경우)인지
 recursive case(바로 답을 알 수 없어서 쪼개서 풀어야 하는 경우)인지 판단해서 
 recursive case인 경우 부분 문제들로 나눈다. 
 

2.conquer

각 부분 문제를 해결 (정복)  (solve them recursively)

divide 후 부분 문제들을 해결 (부분 문제들도 분할정복으로 해결한다.->재귀)

3.combine

부분 문제들의 솔루션을 통해 기존 문제를 해결 
(combine the solutions to get the answer to the problem)

분할정복 문제 적용 .

간단한 예제

1부터 8까지 더하면 몇인가 ? Q(1~8) = ?

Q(1~8) = Q(1~4) + Q(5~8)    -> Q(1~8)은 
                              Q(1~4)와 Q(5~8)의 연산으로 구할 수 있다. (분할)


base_case중 하나인 Q(1~1)    -> 1부터 1까지 더한 것은 1 (정복 ) 


Q(1~2)=Q(1~1)+Q(2~2)        -> 1+2 = 3 (조합 )

백준 1629

10의 11제곱을 12로 나누면 몇인가? Q(10^11 %12)=?

# 방법1. 

10의 11제곱을 12로 모듈러 연산(mod)을 한다.

   10^11 % 12

# 방법2.

분할 정복을 사용한다. 

	Q(10^11 %12) 는 다음 두 가지 수학 법칙을 적용하면
    
        i. 지수법칙 
			
	    10^11=(10^5)∗(10^5∗10)  
			
	    ii. 나머지 분배 법칙
		
	    (AXB)%C =(A%C) * (B%C) % C 

	Q=( Q(10^5 %12)∗Q(10^5∗10 %12) )%12로 구할 수 있다.
    
    즉 Q(10^11 %12)는 Q(10^5 %12)와 Q(10^5*10 %12)의 연산으로 구할 수 있다.(분할)
			
		   *만약 지수가 짝수인 경우 예를 들어 Q(10^12%12) 는 
				 
		   Q=(Q(10^5 %12)∗Q(10^5 %12))%12로 구할 수 있다.
           
    이 문제의 base_case 는 Q(10^1 %12)= 10 (정복 )
    
    Q(10^2 %12) =(Q(10^1 %12) * Q(10^1 %12))%12
                =( 10 * 10 ) %12 = 4 (조합 ) 
                
    
    위 방법을 일반화한 함수는 다음과 같다. 
    
    Q( a^b%c )를 구하는 함수

      a,b,c=map(int,input().split())

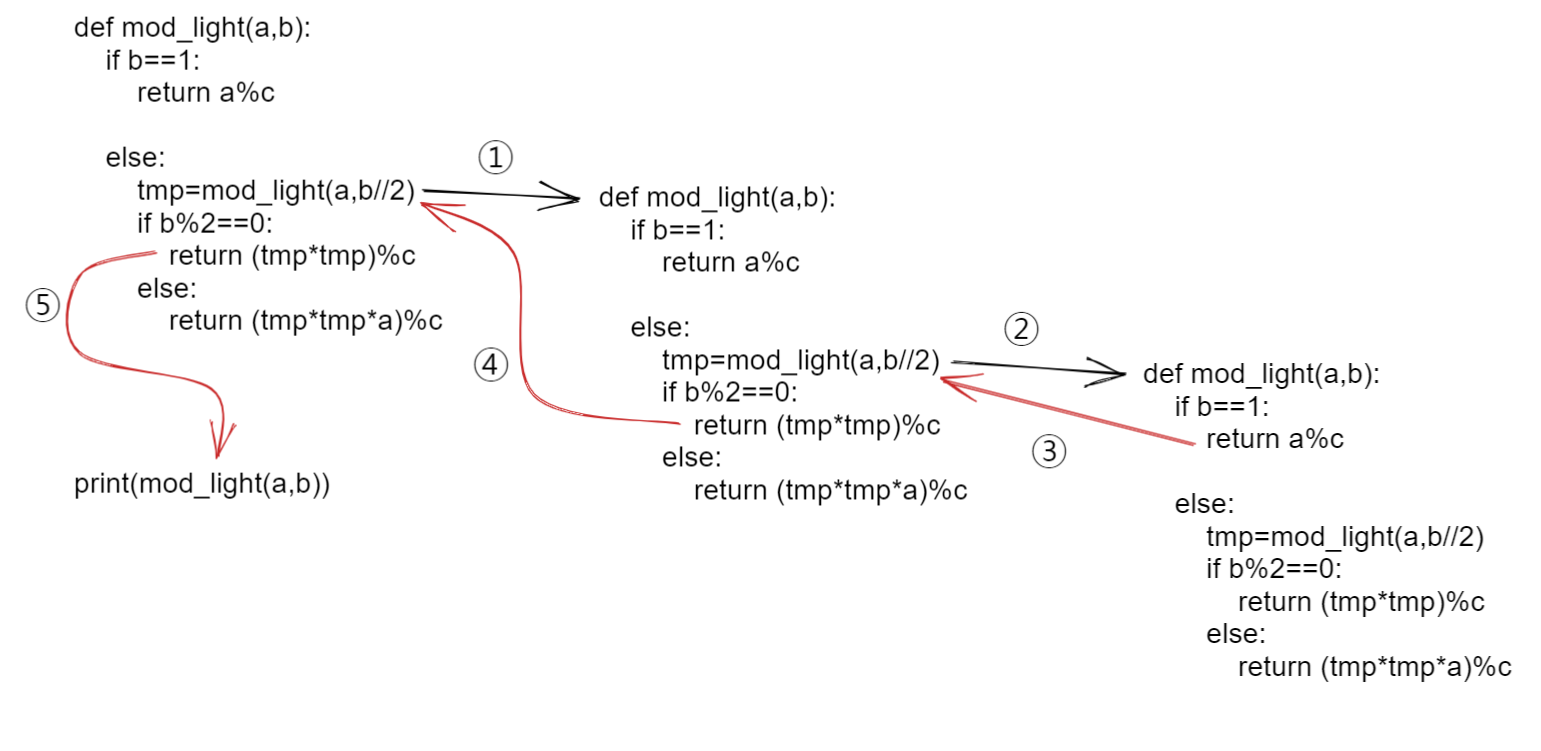
      def mod_light(a,b):
          if b==1:            # base case          
              return a%c      # base case 의 해답 .     

          else:               # recursive case 

              tmp=mod_light(a,b//2)  
              if b%2==0:
                  return (tmp*tmp)%c
              else:
                  return (tmp*tmp*a)%c

함수를 호출하면 다음과 같은 순서로 작동한다.