Introduction
이 논문은 3D human pose estimation (HPE)에서 사용되는 graph convolution networks (GCNs)에 대한 내용이다.
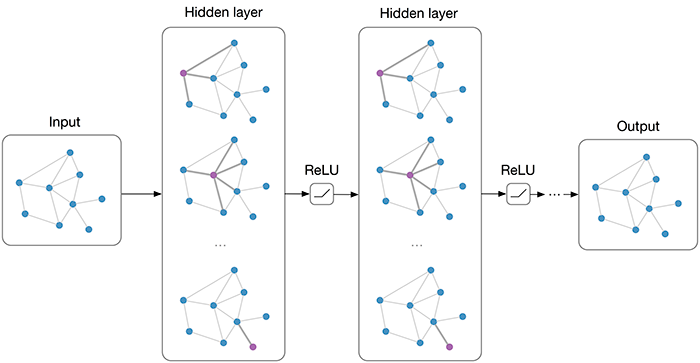
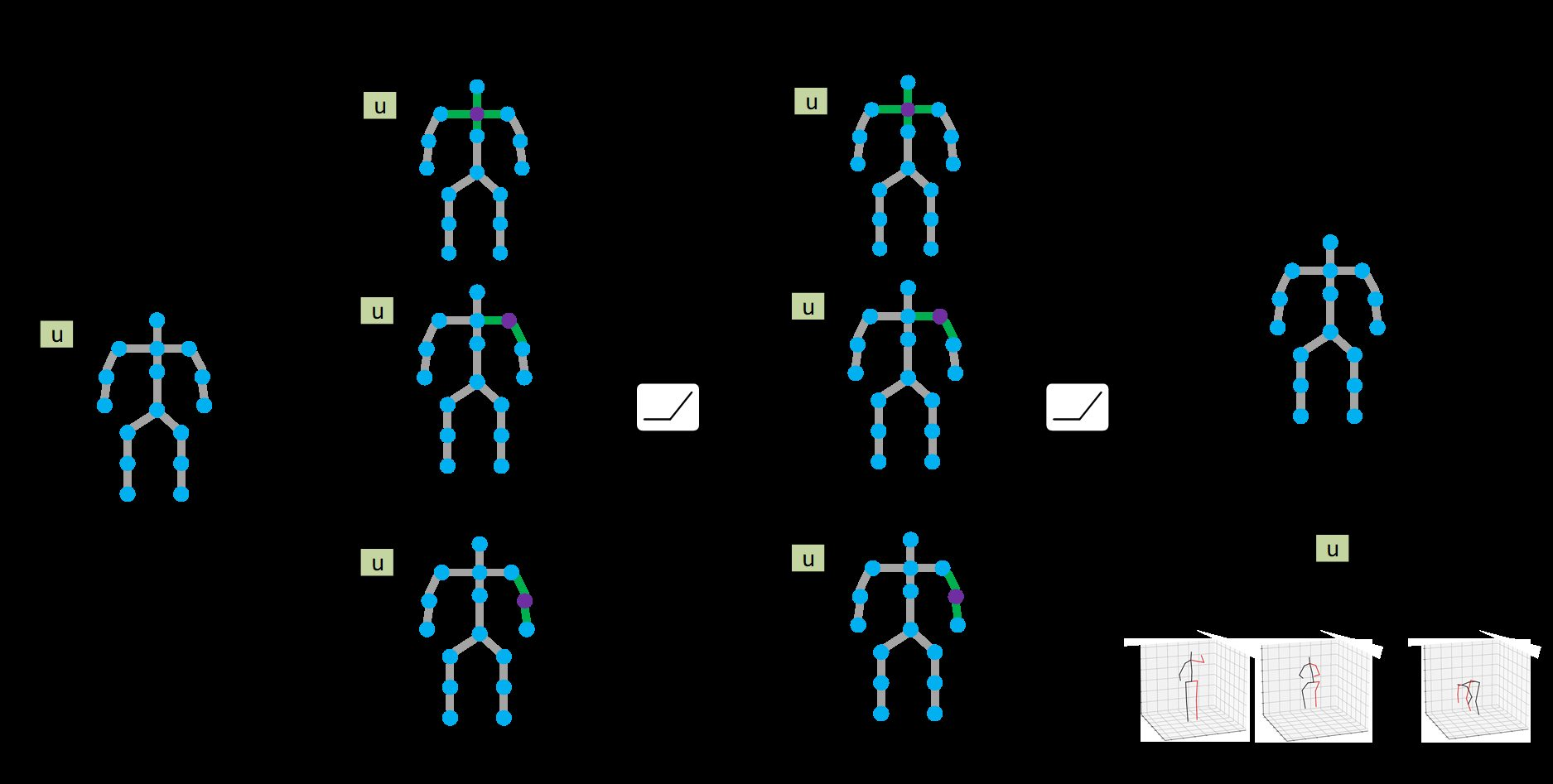
GCNs 는 2D joint detection으로부터 3D human pose를 estimation 하는데 적용되어 좋은 성과를 보여왔다.
Vanilla graph convolution에는 한계가 존재하는데, 인접한 joint와의 관계만 modeling한다. 이는 인접한 joint 외의 다른 joint 간에 다양한 관계를 잘 반영하지 못하기 때문에 비효율적이다.
이 논문은 3D HPE에서의 GCNs가 weight를 공유하는 방법에 대하여 다룬다.
GCN은 feature transformation과 feature aggregation의 수행 순서에 따라 크게 두 가지로 해석이 가능하다.
이 두 가지 해석을 통해, weight sharing methods를 총 다섯 가지로 분류할 수 있게 된다. 여기에 self-connection을 다른 edges와 분리함으로써 세 가지 변형을 추가로 도출할 수 있다.
Human Pose Estimation (HPE)
HPE는 하나의 RGB image로부터 camera 좌표계 상의 human joints 위치를 추정하는 task이다.
3D HPE의 이전 연구들은 input image로부터 direct하게 3D human pose를 regress하는 방식이거나, 2D human pose를 먼저 detection한 후 2D-to-3D pose lifting을 수행하는 two-stage 방식이었다.
최근(이건 2020년도 논문이다) 연구들은 2D-to-3D pose lifting 문제를 푸는데 GCNs을 적용했다. [그림 2] 처럼, 서로 연결된 body joints는 자연스럽게 그래프의 형태를 띄게 되고, joints와 bones는 각각 nodes와 edges를 나타내게 된다.
하나의 GCN은 인접한 body joints의 features에 대하여 transformation과 aggregation을 반복적으로 수행하며 관계를 학습한다. 이는 depth의 ambiguity를 해결할 수 있는 매우 중요한 방식이다.
Fully connected network과 비교했을 때, GCN은 graph nodes를 통한 간결한 표현이 가능하다는 것과, 구조적인 관계를 explicit하게 설명할 수 있다는 점에서 이점이 있다.
그러나 vanilla GCN에는 한계점이 존재하는데, 이는 애당초 graph나 node의 ‘classification’을 위해 설계된 것이기 때문에 모든 node에 대해 단 하나의 feature transformation만을 공유한다는 것이다.
Weight sharing을 통해 보다 간단한 model을 얻을 수 있고 그것의 일반화 성능을 증가시킬 수 있다.
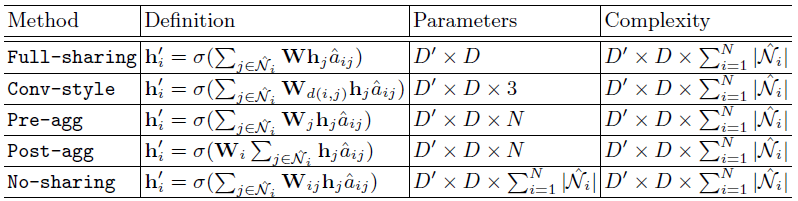
본 논문에서는 다섯 가지 weight sharing 전략을 소개한다. (full-sharing, pre-aggregation, post-aggregation, convolution-style, no-sharing)
- 먼저 full-sharing은 vanilla graph convolution과 동일하다.
- Pre-aggregation은 feature transformation을 먼저 수행한 후 aggregation을 수행하는 방식이다.
- Post-aggregation은 반대의 순서로 진행된다.
- Convolution-style는 CNNs에서 사용되는 convolution 연산에서 motive를 얻은 방식이다.
- No-sharing은 full-sharing과 정확히 반대이고, 두 nodes 사이에 다른 방식의 feature transformation을 정의하게 된다.
GCN에서 사용되는 affinity matrix는 보통 self-connections를 포함한다. 저자들은 서로 관계가 없는 nodes를 분리하였는데, 이를 통해 full-sharing, pre-aggregation, post-aggregation의 변형을 도출해낼 수 있다.
저자들은 실험을 통해 self-connection을 분리하는 것이 성능에 좋은 영향을 미친다는 사실을 발견했고, 같은 parameter 개수를 가진 model이라도 weight sharing 방식에 따라 그 성능이 완전히 달라진다는 사실을 밝혔으며, self-connection이 분리된 pre-aggregation이 3D HPE의 GCNs에서 가장 최적의 weight sharing 방식이라는 것을 알아냈다.
Understanding GCN
GCN은 graph data의 표현을 학습하여 CNN을 일반화한다.
Graph는 다음과 같이 표현된다.
는 N개의 nodes의 집합이고, 는 모든 edges의 집합이다.
모든 edges는 adjacency matrix 로 표현이 가능하다.
는 각 node i와 연관된 D 차원의 feature vector이다.
은 모든 feature vector의 집합을 의미하며, i번째 column이 이다.
GCN은 아래와 같은 공식으로 update된다.
는 update된 feature matrix이고, 차원은 이다. 은 ReLU와 같은 activation function을 의미하며 는 학습 가능한 weight matrix이다. 는 의 normalize된 버전이다.
수식을 해석해보자면, update되는 feature는 현재의 인접한 joints의 features에 weight를 곱한 것이라고 볼 수 있다.
여기서 는 다음과 같이 계산되는데,
는 self-connection을 의미하고 는 degree matrix를 의미한다. Degree matrix란 각 node에 연결된 edge의 개수를 나타내며, 따라서 diagonal matrix가 된다.
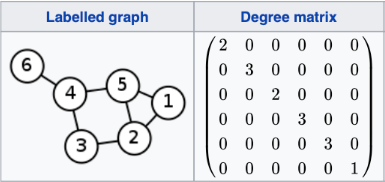
를 의 번 째 원소라고 하고, 와 를 각각 자기 자신을 제외하고 포함한 node 의 neighbors를 나타내는 matrix라고 하면 가 0이 아닐 때만 가 된다. 그렇다면 위에서 를 update하는 수식은 아래와 같이 변형이 가능하다.
수식이 너무 간단해서 해석하기도 애매하지만, 는 결국 업데이트 하고자 하는 column의 번호를 가진 node와 인접한 번호의 column을 의미한다.
위 [그림 3]을 예시로 들면, 을 구하고자 할 땐 는 1이고 은 0이므로, 나머지는 제외하고 만 고려하게 되는 것이다.
이렇게 를 더해서 와 곱하고 activation function을 통과하면 을 구할 수 있는 것이다.
위 수식은 graph convolution을 두 가지 방법으로 해석할 수 있음을 나타낸다.
는 를 곱함으로써 feature를 transformation한 후 을 통해 aggregation을 수행하는 것을 나타내고, 는 feature를 aggregation을 먼저 하고 transformation 한다는 것을 의미한다.
이 두 가지 방법을 통해 총 다섯 가지의 weight sharing 방법을 도출한다.
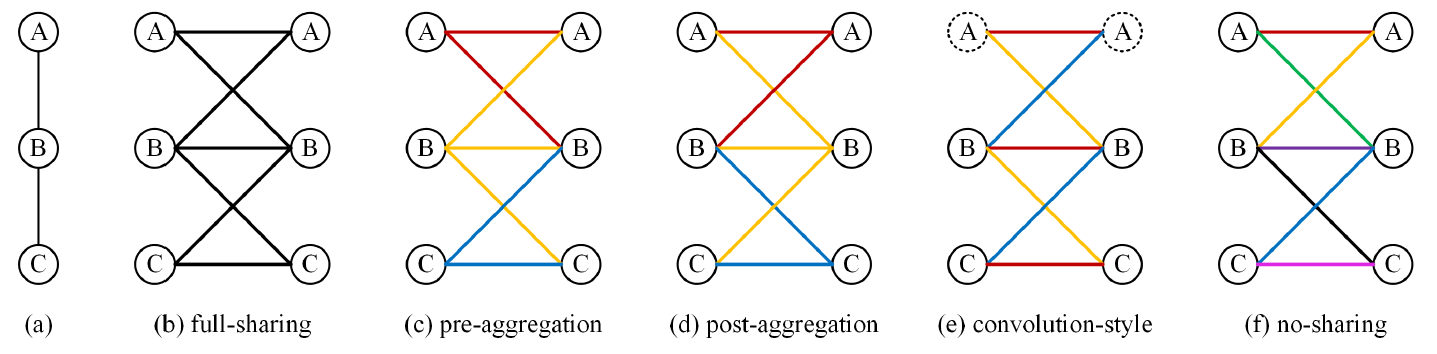
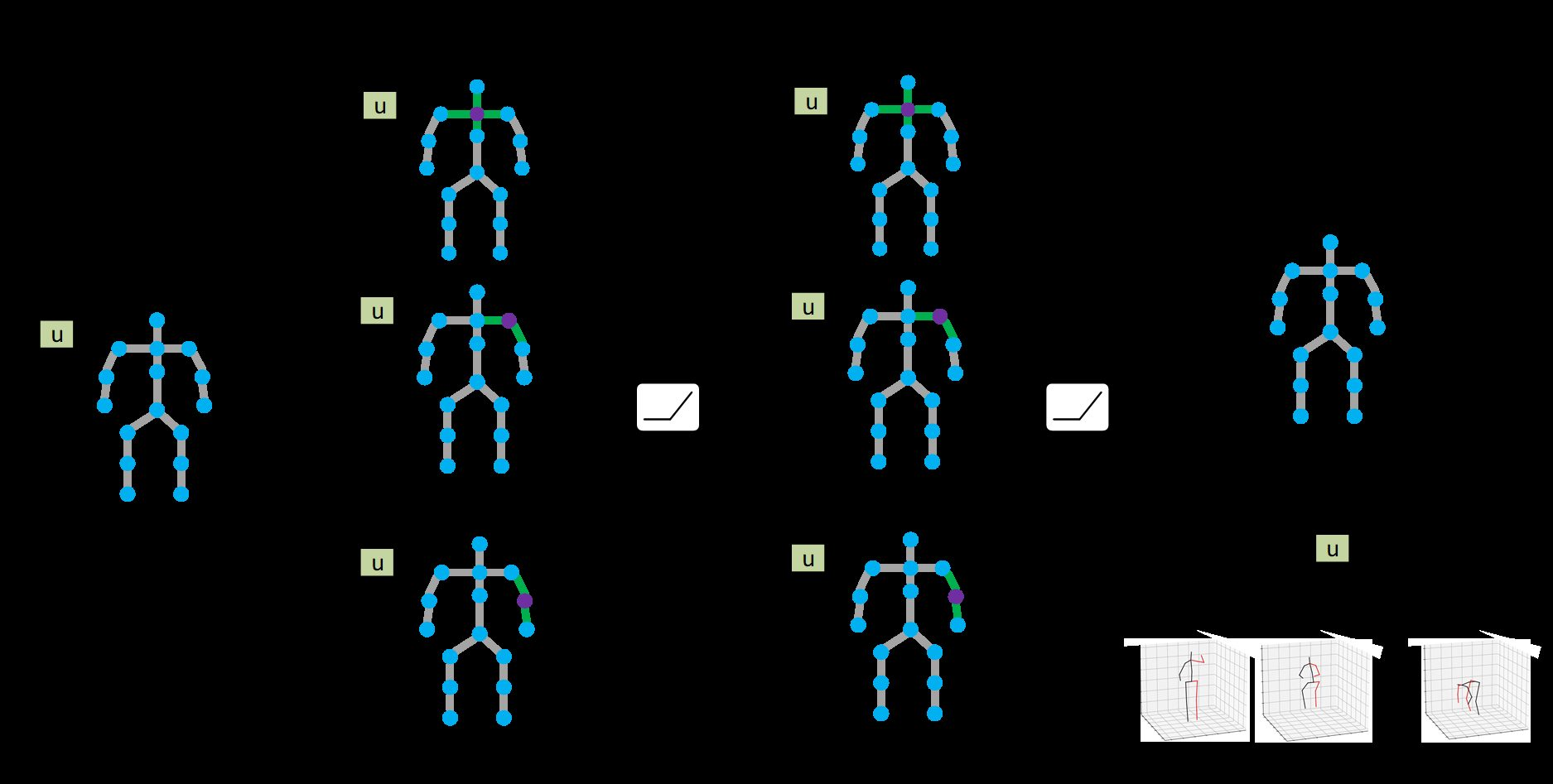
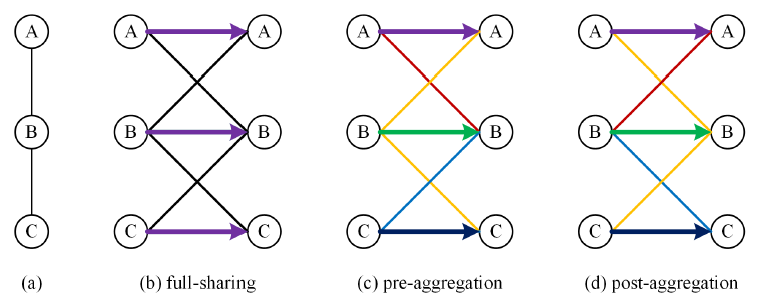
[그림 5]는 graph가 A, B, C의 3개 node로 이루어져 있을 때 각 weight sharing method에 대하여 같은 weight을 같은 색깔로 나타낸 것이다.
Full-sharing
[그림 4]에서 확인할 수 있듯, 위에서 계속 다루었던 수식은 full-sharing이다. Full-sharing은 일반화 성능이 뛰어나고 임의의 구조에 같은 GCN을 적용하여도 비교적 좋은 성능을 보인다. 그러나 사람의 joint들은 멀수록 그 관계성이 적어지는데 반해 full-sharing은 모든 joint에 대해 동등하게 weight를 sharing을 HPE에 대해서는 최적의 방법이 아니다.
Pre-aggregation
Aggregation 이전에 각 node의 input features에 대해 서로 다른 transformation을 진행한다.
는 에 곱해지는 서로 다른 weight matrix를 의미한다.
Post-aggregation
Pre-aggregation과 매우 유사하지만 aggregation 이후 transformation을 진행한다는 점이 다르며, weight matrix가 input feature에 대해 달라지는 pre-aggregation과 달리 update되는 feature에 대해 matrix가 달라진다. (pre: , post: )
Convolution-style
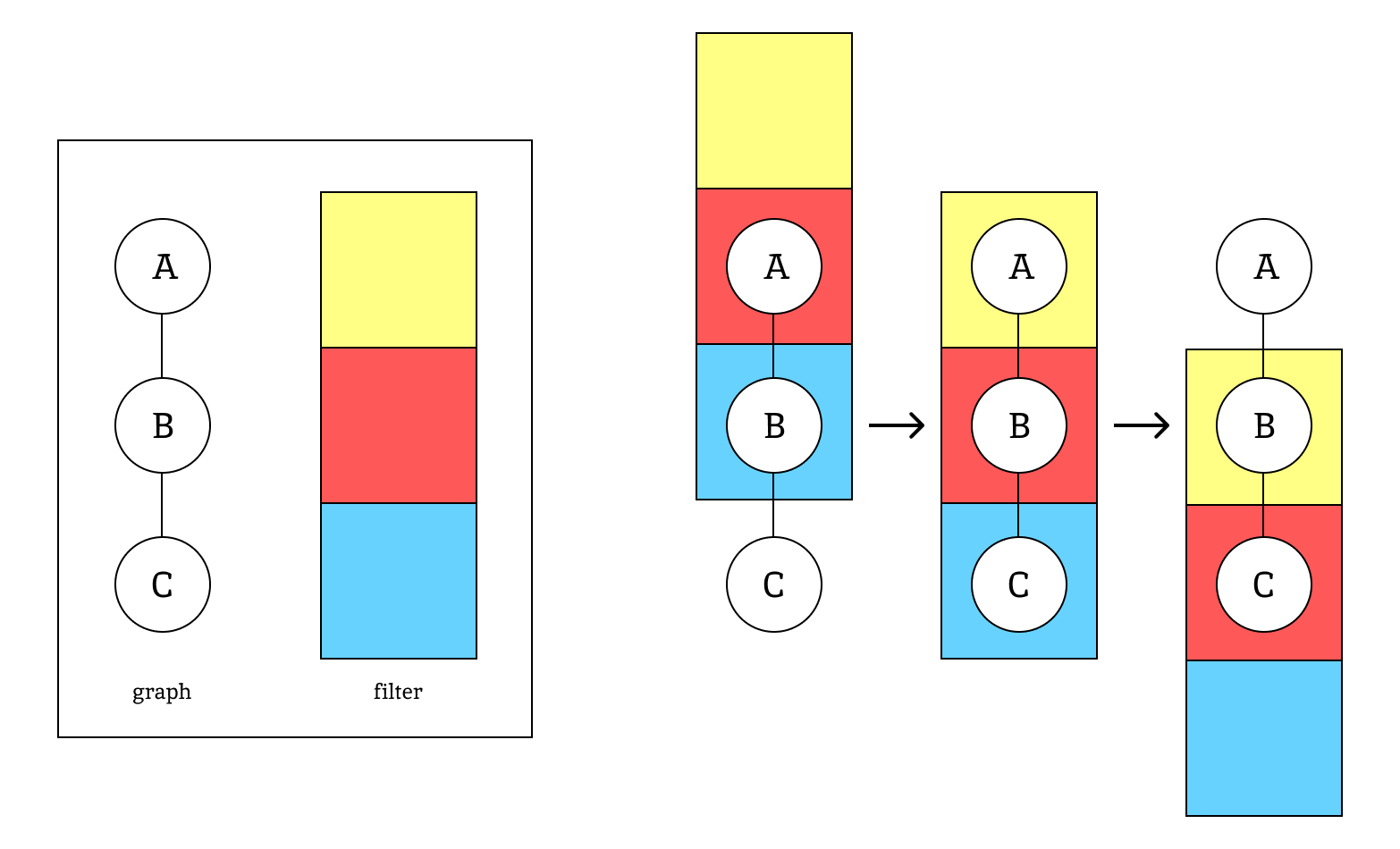
하나의 image는 nodes(pixels)가 grid로 정렬되어 있는, graph의 special case로 볼 수 있다. 이는 grid 상의 2D 좌표에 따라 인접한 pixel을 정의할 수 있게 해주며, image에서 수행되는 convolution을 graph에도 수행할 수 있게 된다.
는 graph의 두 node 를 convolution filter에 올렸을 때의 위치를 의미하는 것 같다. 즉, convolution filter가 움직임에 따라 filter를 기준으로 graph의 nodes의 위치가 계속 변할 것이기 때문에 node 별로 서로 다르게 weight가 곱해지게 된다. 이건 2D convolution을 생각하면 그렇게 어렵진 않은 것 같다. 그림을 그렸는데 좀 허접하긴 하지만,, 아무튼 아래와 같게 된다고 이해할 수 있겠다.
No-sharing
모든 node의 input과 update되는 features에 대해 서로 다른 weight matrix를 적용한다. 이 경우 weight을 전혀 공유하지 않게 된다.
Decouple Self-connections
지금까지는 GCN에 self-connection이 포함된 것을 고려했다. Neighbors와 node를 연결하는 것과는 다르게, self-connection은 당연하게도 서로 다른 nodes 사이의 관계를 modeling하지 않는다. 따라서 논문 저자들은 feature transformation에서 자기 자신의 feature를 따로 분리하여 weight를 곱하는 방식을 실험하였다. 아래 수식은 각각 full-sharing, pre-aggregation, post-aggregation의 변형이다.
는 self-connection을 위한 feature transformation이다. 수식에서 알 수 있듯이 full-sharing은 모든 self-connection에 모두 같은 weight를 곱하는 반면 pre, post-aggregation은 모든 self-connection에 서로 다른 weight를 곱한다.
Network Architecture
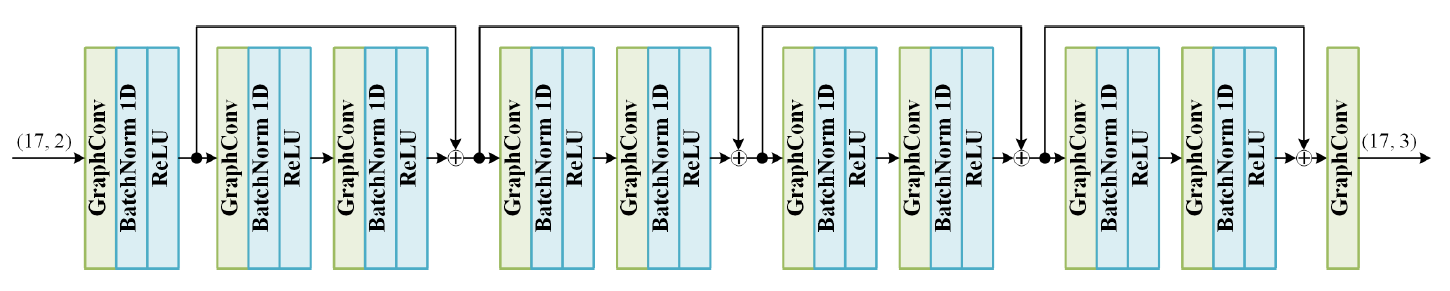
GCN의 input은 image space 상의 body joints의 2D 좌표이고, output은 그에 대응되는 camera 좌표계 상에서의 3D 좌표이다.
입출력이 각각 (17, 2), (17, 3)인 것으로 보아 joints 개수는 17개를 사용하였다.
L2-norm loss를 사용한다.
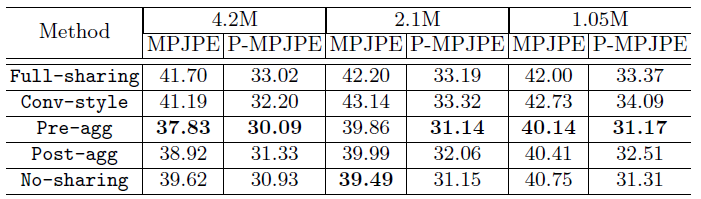
각 GraphConv block에 서로 다른 weight sharing 방법을 사용하였을 때 pre-aggregation이 가장 좋은 성능을 보였고, self-connection을 분리했을 때 더 좋은 성능을 보였다고 한다.