3D human mesh recovery

사람 사진을 한 장 찍는다. 인간이 보면 이 사진에서 사람이 어디에 위치하며 어떤 자세를 취하는 지, 카메라에서 대략 어느 정도 거리에 떨어져 있는 지 알 수 있지만, 컴퓨터가 볼 땐 그저 pixel의 연속일 뿐이다.

3D human mesh recovery (HMR)은 한 장의 사진에서 사람 위치를 파악하고 detect하여, 이 사람의 각 관절에 대한 depth 등 위치 정보와 사람의 체형에 대한 정보를 추출하여 3D mesh의 형태로 복원하는 분야이다. 3D 이므로 다양한 각도에서 보는 것이 가능하다.

개인적으로 이 분야는 메타버스나 헬스케어 등에 사용될 수 있을 것이라고 생각된다.

그림 1. 3D HMR 예시, 출처: Yan, Guoli, Zichun Zhong, and Jing Hua. "Self-Supervised 3D Human Mesh Recovery from a Single Image with Uncertainty-Aware Learning." Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 38. No. 6. 2024.

Introduction

이 논문은 HybrIK라는 걸 사용해서 3D human mesh를 복원하는 새로운 방법을 제시한다.

Monocular RGB image로 3D surface를 복원하는 것은 애초에 ill-posed 문제이지만, SMPL과 같은 좋은 무기가 있다. 이를 통해 몇 개 안되는 parameter를 가지고 현실적이면서도 controllable한 3D mesh를 생성해낼 수 있다.

이러한 model들을 사용한 model-based methods는 일반적으로 두 가지로 나뉜다.

1. Optimization-based approach: 반복적인 fitting을 통해 body pose와 shape을 추정한다. 즉, 2D joint location과 silhouette 등을 추정된 mesh의 2D projection과 비교하며 최적화해 나가는 방식이다. Non-convex 문제이기 때문에 시간이 오래 걸린다는 점과, 결과가 initialization에 민감하다는 것이 단점이다.
2. Learning-based approach: neural network을 사용하여 regression을 통해 직접 model parameter를 찾는다. Neural network을 사용하기 때문에 parameter가 추상적이고, 이로 인해 network이 mapping function을 학습하는 것이 어렵다는 단점이 있다.

Model-based methods의 위와 같은 문제점 때문에 3D keypoint estimation을 사용한다.

3D keypoint methods는 volumetric heatmap을 target representation으로 채택하여 3D joint location을 학습했고, 뛰어난 성능을 보였다.

저자들은 이를 통해 3D joint와 body mesh 사이의 관계를 구축하는데 영감을 얻었다고 한다. 정확한 3D joint는 3D body mesh를 추정하는데 도움이 될 것이고, SMPL과 같은 parametric body model의 shape prior는 3D keypoint estimation methods의 비현실적인 body 구조를 보완한다.

그림 2. HybrIK를 통한 3D skeleton과 parametric model 사이의 loop closing, 출처: 논문

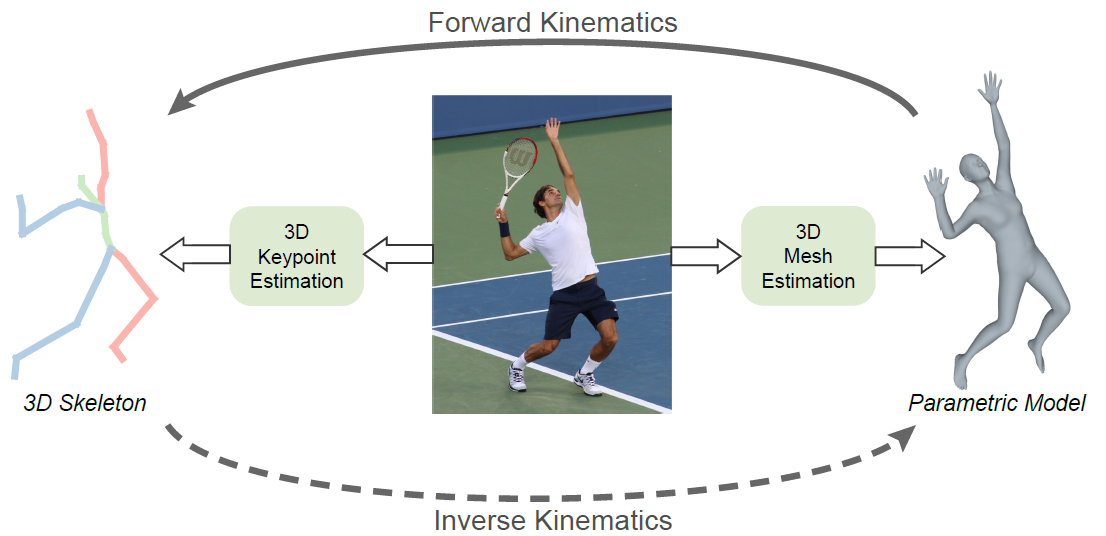
이 논문에서는 hybrid analytical-neural inverse kinematics (HybrIK, [그림 1])라는 solution을 제시하여 3D keypoint estimation과 body mesh estimation 사이의 gap에 다리를 놓아주었다.

Kinematics

Forward kinematics

Forward kinematics는 rest pose template $\bold{T}=\{t_k\}^K_{k=1}$와 relative rotations $\bold{R}=\{R_{pa(k),k}\}^K_{k=1}$을 input으로 하여 reconstructed pose $\bold{Q}=\{q_k\}^K_{k=1}$를 계산하는 과정이다.

$K$는 body joints의 개수이고, $q_k\isin\mathbb{R^3}$는 $k$번째 joint의 reconstructed 3D location, $t_k\isin\mathbb{R}^3$는 rest pose의 $k$번째 joint location, $pa(k)$는 $k$번째 joint의 parent’s index를 의미한다. 따라서 $R_{pa(k),k}$는 $k$번째 joint의 parent joint에 대한 상대적인 rotation을 나타낸다.

FK는 root joint 부터 leaf joints(손, 발 등)까지의 body part를 재귀적으로 회전시키면서 수행된다.

이 때, $R_k\isin\mathbb{SO}(3)$는 canonical rest pose space에 대한 $k$번째 joint의 global rotation을 의미한다. 이는 다음과 같이 계산되는데, 상당히 당연하다.

parent가 없는 root joint의 경우, $q_0=t_0$이 된다.

Inverse kinematics

Inverse kinematics(IK)는 FK와 반대되는 과정으로, rest pose template $\bold{T}$와 body joints $\bold{P}=\{p_k\}^K_{k=1}$를 input으로 하여 relative rotations $\bold{R}$을 계산한다.

$p_k$는 input pose의 $k$번째 joint를 나타내며, 결과로 나온 rotation은 다음과 같은 조건을 만족한다.

$p$와 $q$는 각각 input pose, reconstructed pose라는 점 외에는 동일하다.

이 때도 FK와 마찬가지로 parent가 없는 root joint의 경우, $p_0=t_0$이 된다.

FK는 well-posed인 반면, IK는 target joint location을 만족하는 solution이 많기 때문에 ill-posed problem이다.

SMPL Model

여기서도 human bode의 표현을 위해 SMPL parametric model을 사용한다. shape parameter는 $\beta\isin\mathbb{R}^{10}$, pose parameter는 $K=23$ 개의 joint를 사용하여 $\theta=(\theta_1,\theta_2,\cdot\cdot\cdot\,,\theta_k)$로 modeling되며 이들은 모두 relative rotation이다.

SMPL은 미분 가능한 함수인 $\mathcal{M}(\theta,\beta)$을 제공하여 triangulated mesh $M\isin\mathbb{R}^{N\times3}$을 출력한다. ($N$은 6890개의 vertex를 나타낸다.)

$\bold{Q}_{smpl}=\bold{FK(R,T)}$를 얻게 되며, 앞서 얻은 $M$과 linear regressor인 $W$를 곱하여 Human3.6M의 joint를 얻을 수 있게 된다 ($\bold{Q}_{h36m}=WM$).

Human3.6M 뿐 만 아니라 여러 dataset에 대한 regressor는 인터넷 곳곳에 흩뿌려져 있는 것으로 보인다. 쉽게 구할 수 있다!

Hybrid Analytical-Neural Inverse Kinematics

Relative rotation을 direct하게 regression하여 human body mesh를 추정하는 것은 매우 어려운 일이다. 이 논문 저자들은 HybrIK를 소개하며 이 model을 통해 mesh 추정 작업을 보다 쉽게 할 수 있다고 한다.

3D joint에 대한 relative rotation이 하나가 아니기 때문에, 우선 기존의 rotation을 twist와 swing으로 나누어 인체 해부학적으로 접근한다.

그림 3. HybrIK model architecture, 출처: 논문

Twist-and-Swing Decomposition

그림 4. Illustration of the twist-and-swing decomposition, 출처: 논문

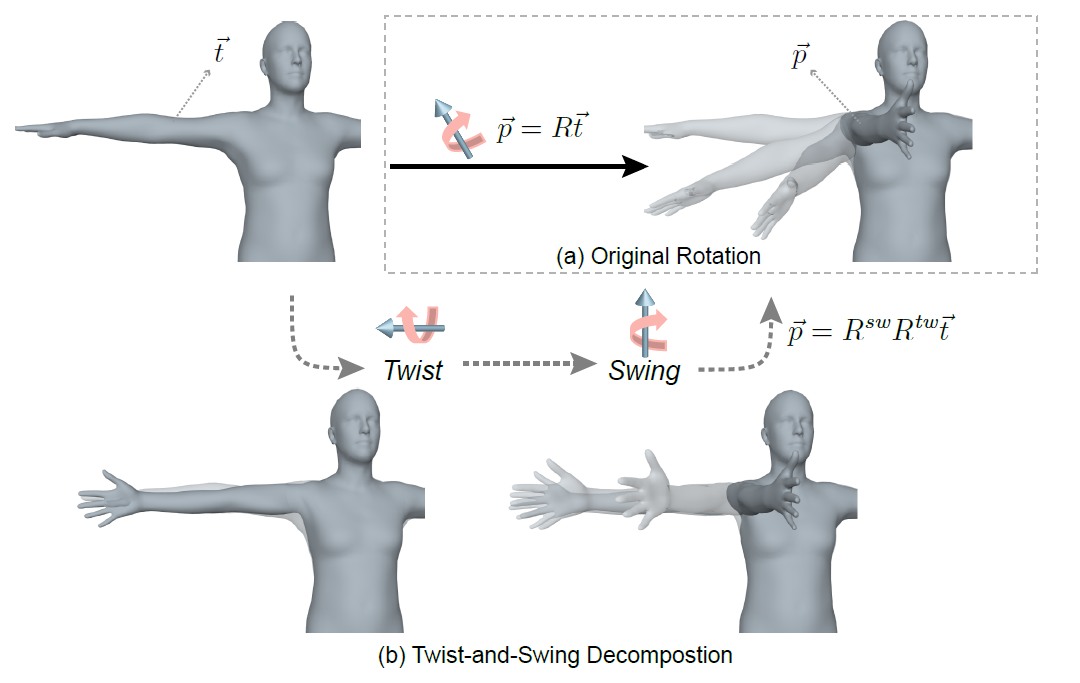
[그림 4]의 (a)와 같이, 원래의 rotation은 하나의 $R$로 이루어졌다. 따라서 하나의 축을 기준으로 회전하기 때문에, 그림의 motion과 같이 이동하게 된다.

(b)는 twist 이후 swing하는 motion을 나타낸다. $R^{sw}, R^{tw}$의 두 rotation으로 이루어져 있는데, (a)의 $R$을 decompose한 것이다.

Start template body-part 벡터를 $\vec{t}$, target 벡터를 $\vec{p}$ 라고 하면, solution process $R$은 다음과 같이 공식화된다.

이 때 $\phi$는 twist angle로, neural network을 통해 추정된다. $\mathcal{D}^{sw}$는 swing rotation의 closed-form solution이며 $\mathcal{D}^{tw}$는 $\phi$를 twist rotation으로 변환하는 함수이다.

여기서 $R$은 위에서 언급한 공식 $p_k-p_{pa(k)}=R_k(t_k-t_{pa(k)})\quad\forall1\le k\le K$ 를 만족해야 하며, 이는 $\vec{p}=R\vec{t}$ 와 같다.

Swing rotation은 $\vec{t}$와 $\vec{p}$ 에 수직인 축 $\vec{n}=\displaystyle\frac{\vec{t}\times\vec{p}}{\Vert\,\vec{t}\times\vec{p}\,\Vert}$이 존재하며, swing angle $\alpha$는 다음을 만족한다.

따라서 Rodrigues formula를 통해 다음과 같이 swing rotation을 구할 수 있다.

$[\vec{t}]_\times$은 $\vec{t}$의 skew symmetric matrix이다.

수식이 좀 복잡한데, 어쨌거나 twist-and-swing 분해의 장점은 3-DoF 회전을 1-DoF의 twist와 swing으로 나누어 학습의 난이도를 줄이고 학습을 용이하게 한다는 점이다.

Naive HybrIK

HybrIK는 naive와 adaptive로 나뉜다. 우선 naive HybrIK에 대한 설명이다.

IK process는 FK와 같이 kinematic tree를 따라 recursive하게 수행될 수 있다. 처음엔 global root ratation $R_0$를 결정한다. 그리고 각 step마다 $R$을 계산하는데, 알고리즘은 다음의 [그림 5]와 같다.

그림 5. Naive HybrIK pseudo code, 출처: 논문

Adaptive HybrIK

Naive HybrIK도 효율적이지만, parent joint의 위치 error가 children joint에도 누적된다는 단점이 있다. Adaptive HybrIK는 각 단계에서 새로 reconstruction된 parent joint를 기준으로 하여 target vector를 동적으로 업데이트하며 error 누적을 방지한다.

그림 6. 오류 누적 관점에서의 naive와 adaptive HybrIK, 출처: 논문

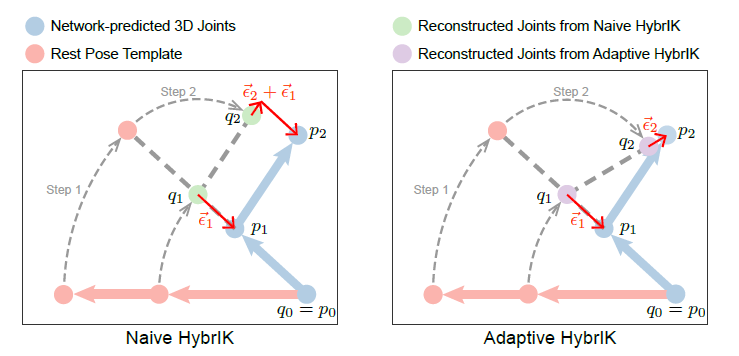
아래 알고리즘을 보면, 매 step마다 joint의 위치를 추정하는 부분이 추가되어 있는 것을 볼 수 있다.

그림 7. Adaptive HybrIK pseudo code, 출처: 논문

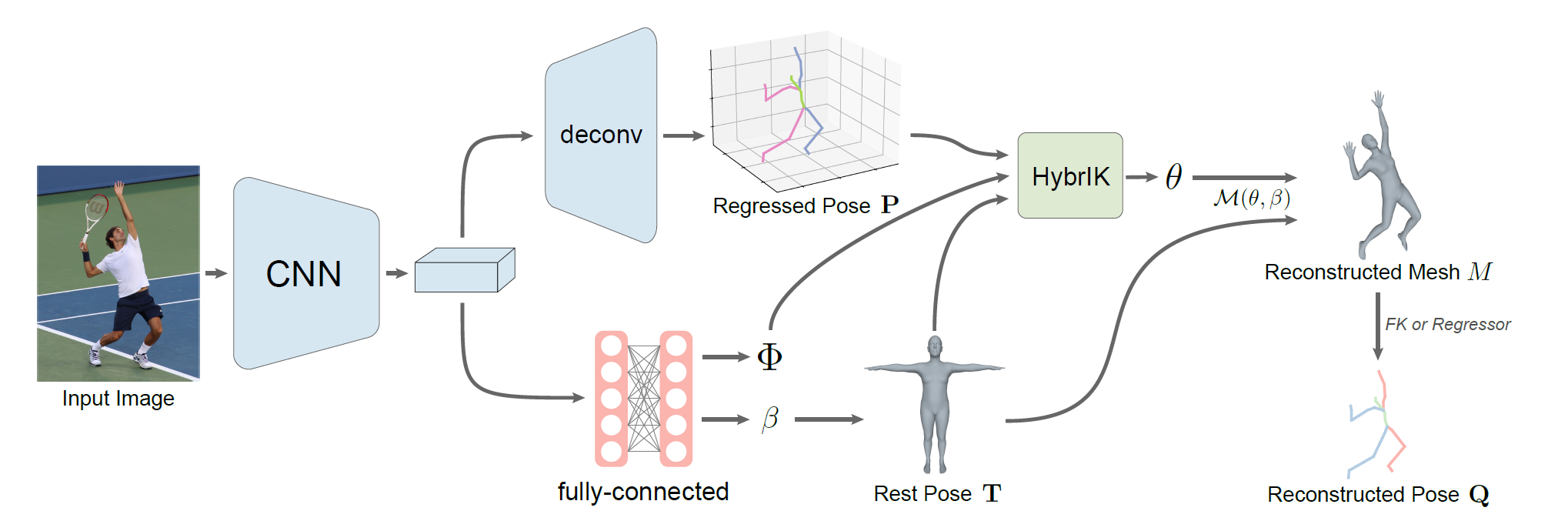
최종적으로, HybrIK process는 joint의 위치를 추정하고, twist angle을 추정하며, 이를 SMPL과 결합하여 shape과 rotation을 추정한다.

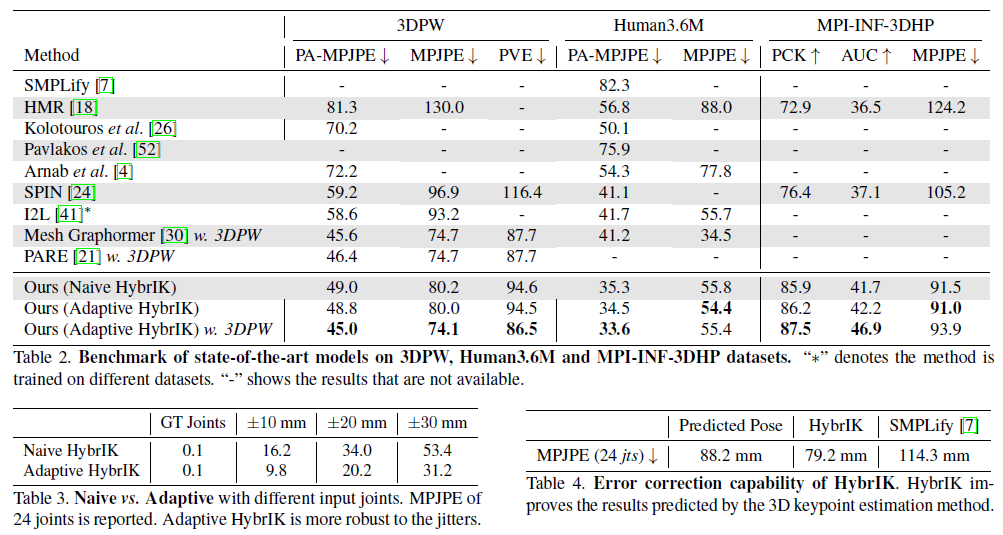
아래 성능을 보면, 다른 methods보다 Adaptive HybrIK가 성능이 가장 좋음을 알 수 있다.

그림 8. HybrIK 성능, 출처: 논문