하노이 탑 이동 순서

링크: https://www.acmicpc.net/problem/1914
분류: 재귀
레벨: Gold 5

---

문제

세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.

1. 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
2. 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.

이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.

아래 그림은 원판이 5개인 경우의 예시이다.

입력

첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 N (1 ≤ N ≤ 20)이 주어진다.

출력

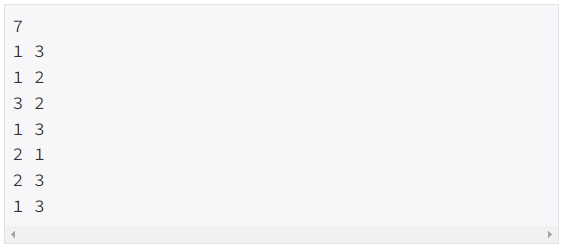
첫째 줄에 옮긴 횟수 K를 출력한다.

두 번째 줄부터 수행 과정을 출력한다. 두 번째 줄부터 K개의 줄에 걸쳐 두 정수 A B를 빈칸을 사이에 두고 출력하는데, 이는 A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위로 옮긴다는 뜻이다.

예제 입력

예제 출력

---

회고

현재 기준 백준 실버3 정도 밖에 안 되는 수준이고 컴공 출신도 아니라
알고리즘이라는 카테고리 자체가 익숙하지 않아서
처음 문제를 봤을 땐 dictionary로 구현해야 하나 싶고 막막했다.

일단은 수학적인 규칙성을 보기로 했는데,
N이 5일 때 정도까지 노가다를 하니 규칙성이 좀 보이기 시작했고
재귀 함수로 풀어야 한다는 느낌이 좀 오기 시작했다.

무작정 풀이를 시작하기 보단 문제의 원리를 파악하는 것이
알고리즘 풀이에 있어 중요한 것 같다.

---

풀이

좀 지저분하긴 한데, 처음 문제를 봤을 때의 막막한 심정이 들어있다...
원리를 우선 파악하여, N개의 원판으로 확장하고자 했다.

일단은 몇 번 원판을 이동하는지 출력해야 하기 때문에 개수를 셌다.
초록색으로 적은 부분이 개수인데, 사실 수학이랑 좀 친하면
2, 4, 8, 16, 32가 바로 보일 것이기 때문에 이 부분은 그렇게 어렵지는 않았다.
이 부분은 재귀함수로 들어가기 전에 바로 print 해버렸다.

import sys

input = sys.stdin.readline
N = int(input())

print(2**N - 1)

위 메모장에서 빨간색, 파란색으로 표시된 부분이 반복되어 나타난다.
이렇게 N이 커짐에 따라서 이전 N이 반복되는 특성이 존재하므로
재귀함수를 써야한다는 건 알겠는데, 초보인 나에게 재귀함수는 너무 어렵다..
일단은 재귀함수를 구현하려면 함수 안에 함수를 넣는 것부터 시작해야 한다고 생각해서..

import sys

input = sys.stdin.readline
N = int(input())

def hanoi(num):
	hanoi(num)

print(2**N - 1)
hanoi(N)

막막함이 모니터를 뚫고 느껴지는 듯 하다 ㅋㅋ

그리고 실제로는 가장 큰 N부터 N-1, ... 차례로 stack에 쌓이지만
구현 시에는 stack의 가장 끝에서부터 계산이 시작되는
1부터 구현하는게 편한 것 같다. 이런 식으로

import sys

input = sys.stdin.readline
N = int(input())

def hanoi(num):
	if num == 1:
    	print(1, 3)
    else:
		hanoi(num)

print(2**N - 1)
hanoi(N)

그런데 이렇게 하고 보니 print(1, 3)이 상당히 거슬린다.
일단 두고 다음 코드를 구현하려고 했는데
다음 단계인 '그럼 만약 저기서 N으로 2가 들어오면 어떻게 될 것인가?'
여기서 바로 N이 2라면 1번 원판이 3번 장대가 아닌 2번 장대로 옮겨진다는 걸 깨달았다.
hanoi 함수에 파라미터를 추가해서 start 장대와 end 장대를 다룰 수 있도록 했다.

시작 시에, N번 원판은 무조건 1번에서 3번으로 이동해야 하기 때문에
초기값은 각각 1, 3으로 설정했다.

import sys

input = sys.stdin.readline
N = int(input())

def hanoi(num, start, end):
	if num == 1:
    	print(start, end)
    else:
		hanoi(num, start, end)

print(2**N - 1)
hanoi(N, 1, 3)

지금부터는 N이 2, 3, 4 등 작은 수가 들어왔을 상황을 가정하고 풀이를 계속했다.
또 깨달았는데, 함수 안의 함수는 N-1일 경우에 대한 함수가 되어야 하기 때문에
예를 들어 N이 2일 경우 내부에 있는 hanoi 함수의 argument는 1, 1, 2가 되어야 한다.
그럼 첫 번째 argument는 num-1이 들어간다는 건 알겠는데,
start, end는 어떻게 설정해야 하는가..?

분명 이전의 start와 end가 힌트가 될 거라 생각하고 조합을 계속 생각했다.
장대는 3개이고, 1번 원판은 2번 원판의 start와 end를 제외한 곳에 위치해야 한다.

즉, N-1번 원판이 움직여야 한다는 것은
N-1번 원판이 N번 원판 위에 위치해서 N번 원판이 움직일 수 없다는 뜻이므로
N-1번 원판의 start는 N번 원판의 start와 같아야 하는 것으로 이해했다.

그리고 장대에는 각각 1, 2, 3이라는 번호가 붙어 있기 때문에,
6에서 N번 원판의 start와 end를 뺀 장대가 N-1번 원판의 end가 된다.

import sys

input = sys.stdin.readline
N = int(input())

def hanoi(num, start, end):
	if num == 1:
    	print(start, end)
    else:
		hanoi(num-1, start, 6-start-end)
        print(start, end)

print(2**N - 1)
hanoi(N, 1, 3)

여기서 끝이 아닌게, 함수를 잘 보면 N이 2, 3, 4일 때 각각 이런 그림이라고 할 수 있다.

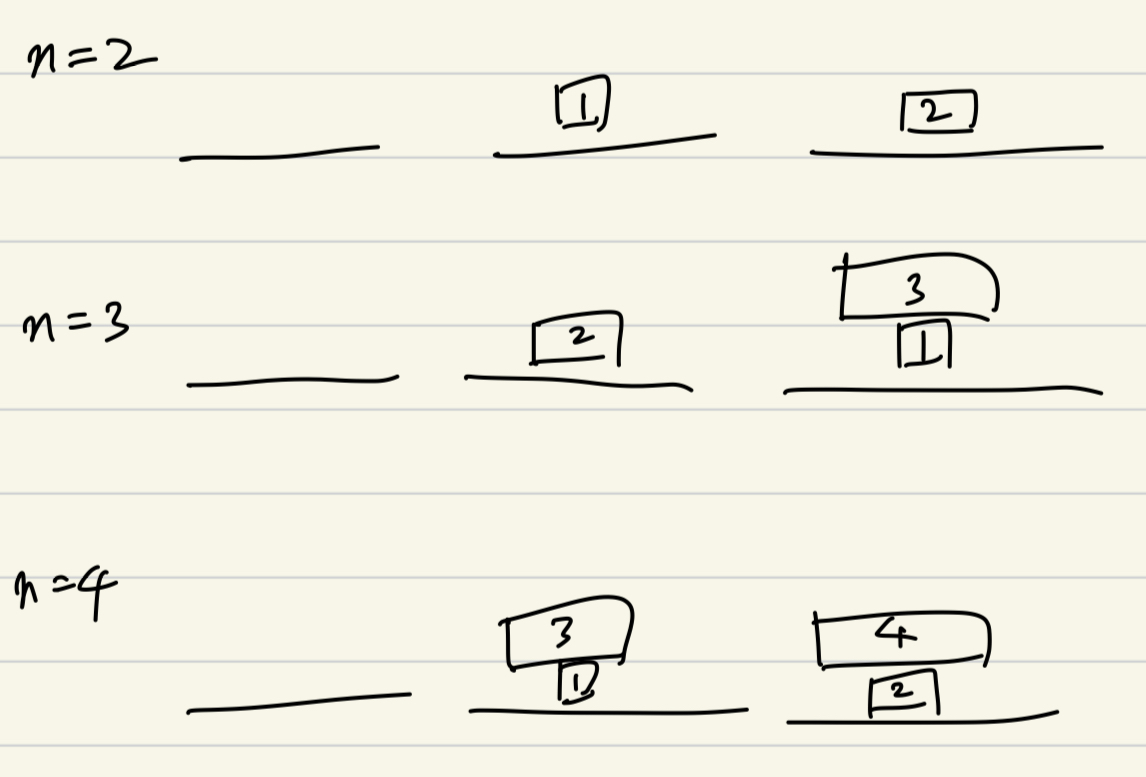
그러니까 N번 원판 위의 원판들을 모두 치웠으면,
2번 장대에 있는 N-1번 원판 위로 모두 다시 쌓아야 하는데
그렇게 하지 않아서 저런 모양새가 나오는 것이다.

해결 방법은 꽤나 간단하다.
N-1번 원판은 처음 end argument로 줬던 6-start-end에 위치해 있을 것이기 때문에
6-start-end를 다시 start로 하고 end 원판으로 옮기면 된다.

최종적인 코드는 아래와 같다.

import sys

input = sys.stdin.readline
N = int(input())

def hanoi(num, start, end):
    if num == 1:
        print(start, end)
    else:
        hanoi(num-1, start, 6-start-end)
        print(start, end)
        hanoi(num-1, 6-start-end, end)
        
print(2**N - 1)
hanoi(N, 1, 3)

코드만 보면 생각보다 많이 간단한데, 수학적인 사고력이 많이 요구돼서 어려웠던 것 같다.