Guided image filter
영상의 필터링을 함에 있어 가우시안 분포 기반의 필터링은 임의로 발생하는 잡음을 자연스럽게 잡아줄 수 있다는 장점이 있다. 가우시안 분포를 이용한 필터링에는 가우시안 필터 뿐만 아니라 양방향 필터(Bilateral Filter), 그리고 결합 양방향 필터(Joint Bilateral Filter)가 존재한다.

위 그림에서 (a)가 가우시안 필터에서의 연산, (b)가 양방향 필터에서의 연산 방법이다. (a)와 달리 (b)에서는 값의 변화가 급격하게 일어난 부분에 대해서는 가우시안 커널의 값을 곱해주지 않았다. 이 부분이 바로 양방향 필터와 가우시안 필터가 갖는 큰 차이점이다. 여기서 나아가 결합 양방향 필터는 가이드 영상을 이용하는 방법이 추가됐는데, 여기서의 가이드 영상은 Ground Truth와 같은 목표하는 결과물을 사용할 수 있다고 한다. 이 필터에 대한 자세한 이야기는 차후에 다루는 쪽으로 하겠다.
이 글에서 다루고자 하는 필터는 Guided Image Filter인데, 이 필터의 가장 큰 장점은 결합 양방향 필터처럼 가우시안 커널과 같은 별도의 커널을 적용하지 않고 가이드 영상 하나를 활용한다는 점이다. 이로 인해 결합 양방향 필터가 갖는 다음의 두 단점을 해결해준다.
- 가우시안 커널을 사용하는 연산이기 때문에 연산 속도가 느리다.
- 영상의 기울기 값 부근에서 왜곡이 발생할 수 있다.
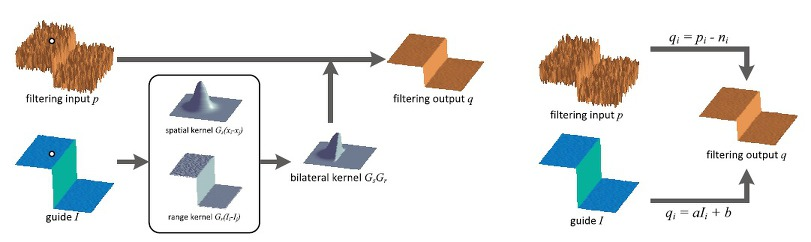
위 그림은 결합 양방향 필터와 가이디드 영상 필터를 이용한 필터링 과정을 대략적으로 보여준다. 앞서 언급했던 가우시안 커널을 응용한 양방향 커널을 사용하는 결합 양방향 필터와는 달리 가이디드 영상 필터링은 Window 크기 내에 있는 픽셀 값들의 평균과 분산, 상관계수 등의 값을 활용한다. 논문에 제시된 알고리즘의 흐름은 다음과 같다.

가이드 영상과 입력 영상에 대한 평균과 분산, 공분산 등을 1,2와 같이 계산한 뒤, a와 b를 정의하고 정의된 a와 b 값에 대해 평균을 구한다. a와 b의 평균값, 그리고 가이드 영상을 이용해 5번 연산을 수행하면 최종 필터링 결과물인 q를 얻을 수 있다. 주석에 나와있듯이 f_mean은 mean filter 결과를 사용한다. 알고리즘에 나와 있듯이, 필요한 연산의 갯수는 결합 양방향 필터에 비해서는 많은 편이다. 그러나 이를 구현하면 속도 면에서는 크나큰 향상을 보일 수 있다.
Fast guided image filter
이 필터는 기존 가이디드 영상 필터에서 파생된 방법으로, 기본 개념은 다운샘플링을 통해 연산 속도를 더욱 향상시킨다는 점이다.

두 필터링 알고리즘을 비교하면 위 사진과 같다. 가이드 영상과 입력 영상의 평균을 구하기 전에 두 영상을 정해진 비율 만큼 다운샘플링하고, 그 결과를 이용해 가이디드 영상 필터링을 수행한다. 이 후의 필터링 과정에 대해서는 a와 b의 평균을 구하는 것 까지는 같으나, 최종 결과물인 q를 얻기 이전에 a와 b의 평균에 대해 다시 원래의 크기로 업샘플링을 수행하고 이 결과물과 가이드 영상을 이용해 최종 결과를 얻는다는 차이가 있다.
References
[1] He, K., Sun, J., & Tang, X. (2013). Guided image filtering. IEEE transactions on pattern analysis and machine intelligence, 35(6), 1397-1409.
[2] https://arxiv.org/abs/1505.00996
