개요
영상 처리에서 장소 인식과 같은 문제를 다룰 때, 내가 만든 프로그램이 얼마나 인식을 잘 하는지를 판별하기 위해 precision과 recall을 모두 활용한다고 한다. 물론 이와 같은 수치는 딥 러닝 분야에서도 지표로 많이 활용된다고 들었다. (딥알못입니다 ㅠㅠ) 간단하게 말하자면, precision은 식별기가 얼마나 정확하게 인식을 수행해냈는가, recall은 식별기가 대상을 얼마나 검출해냈는가라고 할 수 있다.
(이 글을 이전에 티스토리에 끄적이던 글을 옮겨온 것으로, 작성된 지 꽤 지났던 글이라 어쩌면 수정이 필요한 부분이 다소 있을 수 있다. 지속적으로 업데이트를 할 예정.)
간단한 예시
하나의 예로 여러 장의 사진을 입력으로 받으면 그 영상 내에서 의자를 검출해내는 식별기 A와 B가 있다고 가정해보자.
A의 경우, 여러 장의 사진을 지속적으로 받으면서 그 영상에 있는 객체에 대해서 B보다 더 많고 확실하게 추출해낸다. 그렇다면 이 식별기는 식별기 B보다 검출율(Recall)이 좋다고 할 수 있다. 그러나 A가 검출한 객체에서는 분명하게 의자인 객체도 존재하지만, 의자가 아닌 객체가 검출되는 경우도 종종 발생한다. 결국 이 A는 정확도(Precision) 면에서는 그리 좋다고 할 수가 없다.
반대로 B의 경우, 같은 수의 사진을 입력으로 받을 때 A보다는 상대적으로 훨씬 적은 양의 객체를 추출해낸다. 이로 인해 우리는 이 B의 검출율이 A보다 떨어진다는 것을 알 수 있다. 그러나 전체 검출된 객체에 대해서 이 객체가 의자일 확률을 계산할 때, B에서 검출된 객체가 의자인 확률이 압도적으로 높다면 이 식별기 B는 A보다 정확도가 좋다고 할 수 있다.
그렇다면 이 예에서 식별기 A와 B 중 어느 식별기의 성능이 좋은 것일까?
정답은 없다. 좋은 식별기라면 사실 검출율과 정확도를 모두 고려해야하기 때문이다. 정확도가 높아도 분명히 존재하는 객체들을 많이 추출해내지 못한다면, 반대로 검출을 많이해도 그 정확도가 떨어진다면, 이 두 경우는 좋은 식별기라고 할 수 없다.
따라서 객체 등을 인식하는 식별기를 만들기 위해서는 이 두 요인을 모두 고려해야만 한다.
Precision and recall
이렇게 예를 들어서 설명한 정확도와 검출율을 수학적으로 표현을 하자면 다음과 같이 나타낼 수 있다.
식을 보면 네 가지 용어에 대해 적혀있다. True Positive, True Negative, False Positive, False Negative에 대한 설명은 아래 표를 보면 이해를 할 수 있다.
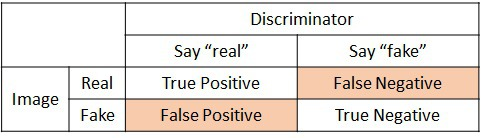
이에 대해서 이해를 할 때, "True"는 참, "False"는 거짓, "Positive"는 긍정적인 대답, "Negative"는 부정적인 대답이라고 여기면 된다.
좀 더 쉽게 이해를 돕기 위해 어떤 임의의 입력 영상이 진짜인지 가짜로 만들어진 것인지 판별하는 작업을 예로 들어 설명하겠다. 임의의 식별기가 임의의 입력 영상을 받게 되고, 진짜 가짜 여부를 검사한 뒤에 그에 대한 답을 내려줄 것이다. 식별 결과, 이 영상이 진짜 영상이라면 식별기는 긍정적인 대답(Positive)를 내놓을 것이고, 가짜 영상이라면 부정적인 대답(Negative)를 내놓을 것이다. 자, 그럼 이제 이 대답이 정답인지 오답인지를 판별해야한다. 만약에 식별기의 대답이 정답이면 "True", 오답이면 "False"가 되는 것이다.
즉, 위의 표에 있는 네 가지 경우를 정리하면 다음과 같이 말할 수 있다.
True Positive : 긍정적인 대답을 내놓았는데, 그게 참이다.
True Negative : 부정적인 대답을 내놓았는데, 그게 참이다.
False Positive : 긍정적인 대답을 내놓았는데, 그게 거짓이다. (Type I Error)
False Negative : 부정적인 대답을 내놓았는데, 그게 거짓이다. (Type II Error)
 (사진 출처 : https://marginalrevolution.com/marginalrevolution/2014/05/type-i-and-type-ii-errors-simplified.html)
(사진 출처 : https://marginalrevolution.com/marginalrevolution/2014/05/type-i-and-type-ii-errors-simplified.html)
아마 위의 사진을 보면 두 에러 케이스에 대해 이해하기 쉬울 것이다(...)
다시 앞서 언급했던 식으로 넘어가서, Precision 식의 분모를 보면 True Positive와 False Positive 값을 모두 합했다. 즉, 분모에는 식별기가 긍정적인 대답을 내놓은 모든 경우가 값으로 들어간다. 반대로 Recall의 분모에서는 True Positive와 False Negative를 더했는데, 이는 식별기가 진짜 영상을 검출한 모든 경우를 의미한다. 정리하자면, Precision 식은 식별기가 진짜라고 검출한 모든 이미지에 대해 얼마나 정확하게 진짜를 검출했는가를, Recall은 식별기가 검출한 모든 진짜 영상에 대해 식별기가 얼마나 정확한 답을 많이 내놓았는가를 의미한다고 보면 된다.
Precision-recall curve
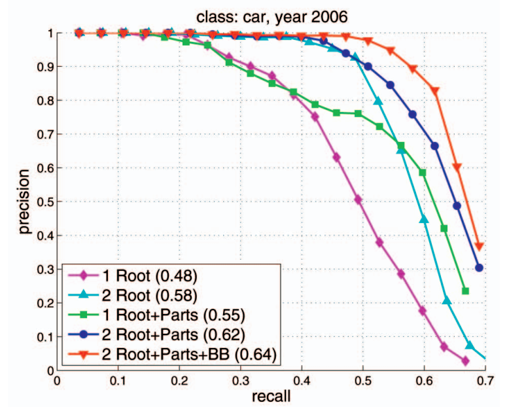 (사진 출처 : Felzenszwalb, P. F., Girshick, R. B., McAllester, D., & Ramanan, D. (2010). Object detection with discriminatively trained part-based models. IEEE transactions on pattern analysis and machine intelligence, 32(9), 1627-1645.)
(사진 출처 : Felzenszwalb, P. F., Girshick, R. B., McAllester, D., & Ramanan, D. (2010). Object detection with discriminatively trained part-based models. IEEE transactions on pattern analysis and machine intelligence, 32(9), 1627-1645.)
위의 그래프는 Precision과 Recall의 상관관계를 그래프로 나타낸 것이다. 그래프에도 나와 있듯이, Precision과 Recall은 서로 반비례의 관계를 보인다. 어떤 식별기에 대해서 이 식별기의 검출율을 높히도록 파라미터를 조절했다고 하자. 그렇게되면 더 많은 양을 검출해낼 수는 있겠지만, 이 중에는 분명 잘못된 결과들도 섞여있을 것이고, 그 수는 검출되는 결과물이 많을 수록 증가할 것이다. 이로 인해 이 식별기의 정확도는 감소할 것이다. 반대로 식별기의 정확도를 높이고자 파라미터를 조절했다고 가정하면 정확한 답만을 더 담고, 부정확한 답들은 제외해야 할텐데 이를 위해서는 검출되는 결과물이 적어질 수 밖에 없을 것이다.
이 그래프를 이용하면 하나의 알고리즘 성능에 대한 파악은 가능하겠으나, 여러 알고리즘을 두고 정량적인 비교를 하려면 어려움이 따를 것이다. 이러한 정량적인 비교를 위해 등장한 개념이 바로 Average Precision이다. 위의 그래프에서 Average Precision은 그래프로 인해 만들어질 수 있는 그래프 아랫 부분의 면적을 의미한다. 여러 알고리즘의 정확도 성능을 비교할 때는 주로 이 값을 활용한다.
