[백준] 10423 전기가 부족해

백준 10423 전기가 부족해

• https://www.acmicpc.net/problem/10423

• 어느 한 도시가 두 개의 발전소에서 전기를 공급받으면 낭비가 되므로 케이블이 연결되어있는 도시에는 발전소가 반드시 하나만 존재해야 한다

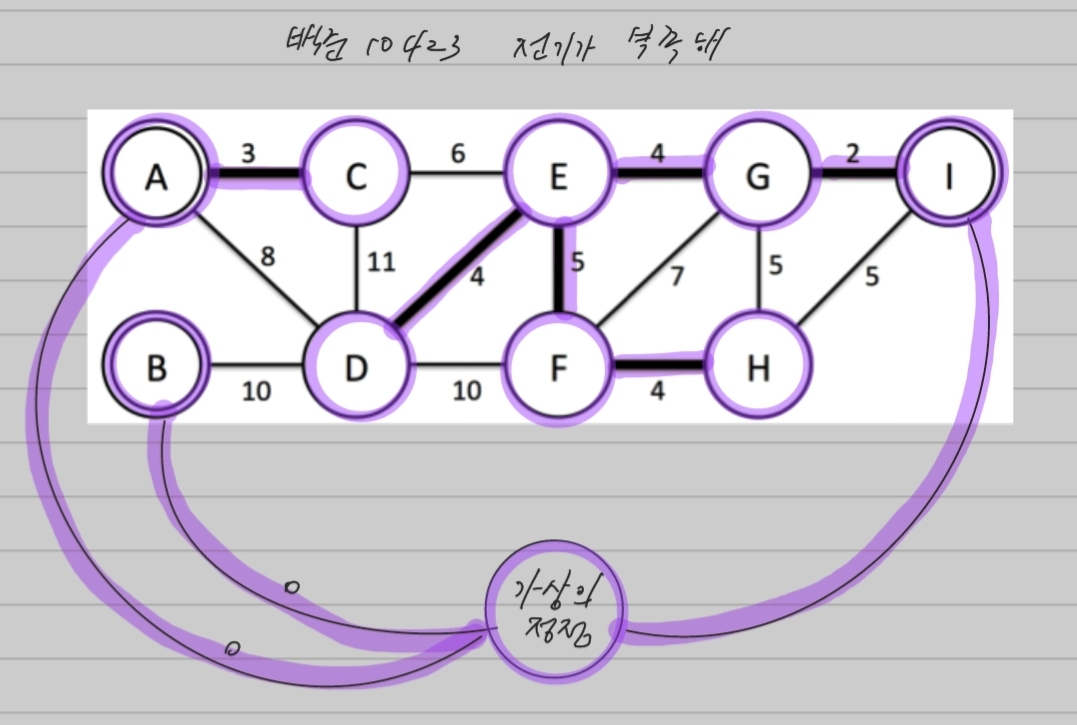
• 가상의 정점을 만들어 그래프 내의 모든 발전소와 가중치가 0인 간선으로 연결한다
  -> 도시가 두 개의 발전소와 연결된 경우 사이클이 발생하게 되므로,
  모든 도시가 하나의 발전소와 연결되어있는 최소 스패닝 트리를 만들 수 있게 된다.

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

typedef long long ll;
const int MAX_V = 1001;

struct DisjointSet {
	vector<int> parent, rank;
	DisjointSet(int n) : parent(n), rank(n, 1) {
		for (int i = 0; i < n; ++i)
			parent[i] = i;
	}

	//u가 속한 트리의 루트 번호 반환
	int find(int u) {
		if (u == parent[u]) return u;
		return parent[u] = find(parent[u]);
	}

	//u가 속한 트리와 v가 속한 트리를 합친다
	void merge(int u, int v) {
		u = find(u); v = find(v);

		//u와 v가 이미 같은 트리에 속하는 경우 걸러냄
		if (u == v) return;

		if (rank[u] > rank[v]) swap(u, v);
		parent[u] = v;
		if (rank[u] == rank[v]) ++rank[v];
	}
};

//정점의 개수
int V;

//그래프의 인접 리스트 (연결된 정점 번호, 간선 가중치) 쌍 저장
vector<pair<int, ll>> adj[MAX_V];

//주어진 그래프에 대해 최소 스패닝 트리 가중치의 합을 반환한다.
ll kruskal() {
	ll ret = 0LL;

	//<가중치, <u, v>>의 목록을 얻는다
	vector<pair<ll, pair<int, int>>> edges;

	for (int u = 0; u < V; ++u) {
		for (int i = 0; i < adj[u].size(); ++i) {
			int v = adj[u][i].first;
			ll cost = adj[u][i].second;
			edges.push_back({ cost, {u, v} });
		}
	}
	//가중치순으로 정렬
	sort(edges.begin(), edges.end());

	//처음엔 모든 정점이 서로 분리되어 있다.
	DisjointSet sets(V);

	for (int i = 0; i < edges.size(); ++i) {
		ll cost = edges[i].first;
		int u = edges[i].second.first;
		int v = edges[i].second.second;

		//간선 (u, v)를 검사한다.
		//이미 u와 v가 연결되어있을 경우(사이클) 무시
		if (sets.find(u) == sets.find(v)) continue;

		sets.merge(u, v);
		ret += cost;
	}

	return ret;
}

int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);
	
	//간선의 개수
	int M;
	//케이블의 개수
	int K;

	cin >> V >> M >> K;
	
	//입력으로 주어지는 도시 1~N번
	//발전소끼리 연결하기 위한 가상의 도시 0번
	//따라서 총 정점의 개수 = N + 1
	V++;

	//발전소
	for (int i = 0; i < K; ++i) {
		int input;
		cin >> input;

		adj[0].push_back({ input, 0LL});
		adj[input].push_back({0, 0LL});
	}

	//케이블
	for (int i = 0; i < M; ++i) {
		int u, v;
		ll w;
		cin >> u >> v >> w;

		adj[u].push_back({ v, w });
		adj[v].push_back({ u, w });
	}

	cout << kruskal();

	return 0;
}