*코드 설명은 주석처리로 되어있습니다.
1) 그래프의 표현
그래프: 연결되어 있는 객체 간의 관계를 표현하는 자료구조
(ex. 트리, 지하철 노선도..)
구성요소: 정점(verices), 간선(edge)
종류: (간선의 종류에 따라) 무방향 그래프, 방향 그래프, 가중치 그래프(간선에 비용/가중치 할당), 부분 그래프
그래프 표현:
-ADT:
데이터 - 정점, 간선의 집합
연산 -
create(): 그래프 생성
isEmpty(): 그래프가 공백 상태인지 확인
insertVertex(v): 그래프에 정점 v 삽입
insertEdge(u,v): 그래프에 간선 (u,v) 삽입
deleteVertex(v): 그래프의 정점 v 삭제
deleteEdge(u,v): 그래프의 간선 (u,v) 삭제
adjacent(v): 정점 v에 인접한 모든 정점의 집합 반환
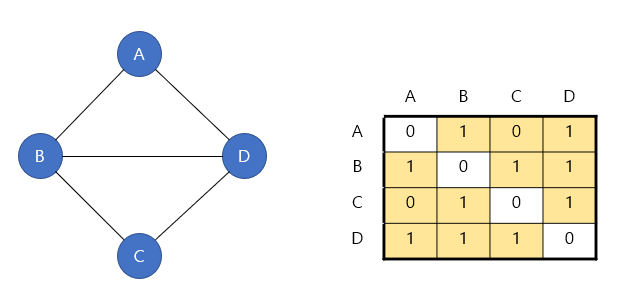
- 인접행렬(M) 활용
간선 존재0 - M[i][j] = 1,
간선 존재X - M[i][j] = 0
 코드구현:
코드구현:
#define MAX_VTXS 100
class AdjMatGraph {
protected:
int size; //정점의 개수
char vertices[MAX_VTXS]; //정점의 이름
int adj[MAX_VTXS][MAX_VTXS];//인접행렬
public:
AdjMatGraph( ) { reset(); }
char getVertex(int i) { return vertices[i]; }
int getEdge(int i, int j) { return adj[i][j]; }
void setEdge(int i, int j, int val) { adj[i][j] = val; }
bool isEmpty() { return size==0; }
bool isFull() { return size>=MAX_VTXS; }
// 그래프 초기화 ==> 공백 상태의 그래프
void reset() {
size=0;
for(int i=0 ; i<MAX_VTXS ; i++ )
for(int j=0 ; j<MAX_VTXS ; j++ )
setEdge(i,j,0);
}
// 정점 삽입
void insertVertex( char name ) {
if( !isFull() ) vertices[size++] = name; //포화상태가 아닐 경우에 새로운 정점 추가
else cout<< "Error: 그래프 정점 개수 초과\n";
}
// 간선 삽입: 무방향 그래프의 경우임.
void insertEdge( int u, int v ) {
setEdge(u,v,1);
setEdge(v,u,1);
}
// 그래프 정보 출력 (화면이나 파일에 출력)
void display( FILE *fp = stdout) {
printf(fp, "%d\n", size); // 정점의 개수 출력
for( int i=0 ; i<size ; i++ ) { // 각 행의 정보 출력
fprintf(fp,"%c ", getVertex(i)); // 정점의 이름 출력
for( int j=0 ; j<size ; j++ ) // 간선 정보 출력
fprintf(fp, " %3d", getEdge(i,j));
fprintf(fp,"\n");
}
}
};- 인접 리스트 활용
각 정점이 연결리스트를 가지고, 인접한 정점들을 연결리스트로 표현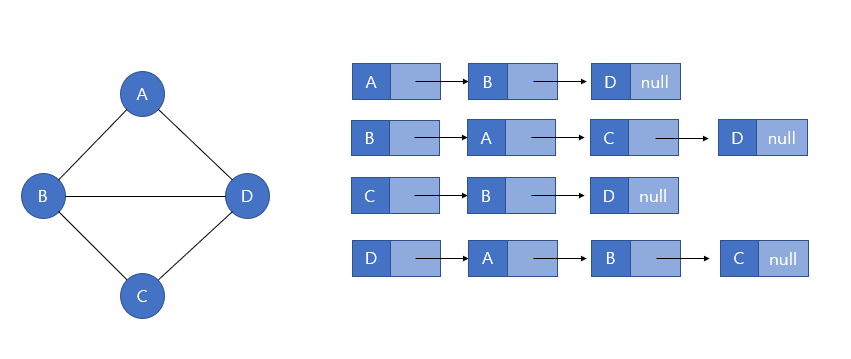
구현:
//Node.h
#define MAX_VTXS 100
class Node {
protected:
int id; // 정점의 id
Node* link; // 다음 노드의 포인터
public:
Node(int i, Node *l=NULL) : id(i), link(l) { }
~Node() {
if( link != NULL ) delete link;
}
int getId() { return id; }
Node* getLink() { return link; }
void setLink(Node* l) { link = l; }
};
#include "Node.h"
#define MAX_VTXS 256
class AdjListGraph {
protected:
int size; // 정점의 개수
char vertices[MAX_VTXS]; // 정점 정보
Node* adj[MAX_VTXS]; // 각 정점의 인접 리스트 (각 노드에 대한 인접 리스트 헤더 포인트 배열)
public:
AdjListGraph() : size(0) { }
~AdjListGraph(){ reset(); }
void reset(void) {
for( int i=0 ; i<size ; i++ )
if( adj[i] != NULL ) delete adj[i];
size = 0;
}
void insertVertex( char val ) { // 정점 삽입 연산
if( !isFull() ) {
vertices[size] = val;
adj[size++] = NULL;
}
else printf("Error: 그래프 정점 개수 초과\n");
void insertEdge( int u, int v) { // 간선 삽입 연산
adj[u] = new Node (v, adj[u]); // 인접 리스트에 추가
adj[v] = new Node (u, adj[v]); // 방향 그래프 ==> 주석 처리함
}
void display( ) {
printf("%d\n", size); // 정점의 개수 출력
for( int i=0 ; i<size ; i++ ) { // 각 행의 정보 출력
printf("%c ", getVertex(i)); // 정점의 이름 출력
for( Node *v=adj[i] ; v != NULL ; v=v->getLink() )
printf(" %c", getVertex(v->getId()) );
printf("\n");
}
}
Node* adjacent(int v) { return adj[v]; } 2) 다익스트라 알고리즘 (최단 경로 문제)
다익스트라 알고리즘: 시작 정점 v에서 다른 모든 정점까지의 최단 경로를 찾는 알고리즘
아이디어:
-적은 가중치를 먼저 선택
-이미 찾은 최단경로를 업데이트 하면서 최종 최단경로를 찾아감
구성요소:
- 시작정점 v
- 집합 S: 최단 경로를 찾은 정점들의 집합
- dist[u]: (v에서 u로) S에 있는 정점들을 거쳐서 간 최단거리
진행 단계:
1. S에 시작점 추가 & dist[u] 값에 간선이 있으면 weight(v,u) 없으면 무한대 값 으로 초기화
2. 인접 노드들에서 S에 없는(방문하지 않은) 정점들 중 dist값이 가장 작은 정점 S에 추가
3. dist값 비교 후 더 작은 값으로 업데이트
2,3 반복
예시를 통해 과정을 알아보자면,
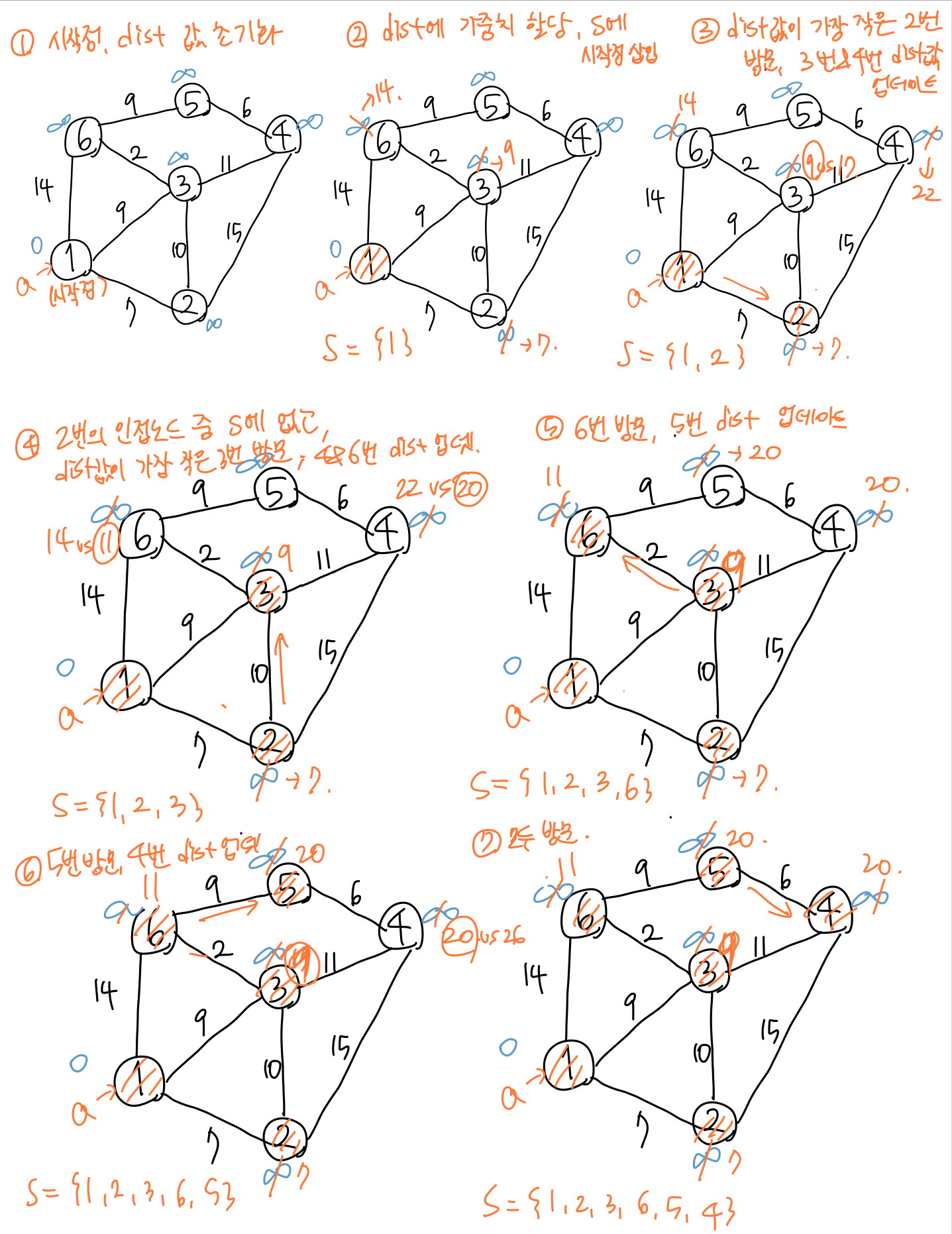
pseudo 코드:
S <- {v}
for 각 정점 w in G do
dist[w] = weight[v][w]
while 모든 정점이 S에 포함되지 않으면 do
u <- 집합 S에 속하지 않는 정점 중에서 최소 dist를 갖는 정점 선택
S <- S union {u}
for u에 인접하고 S에 있지 않은 모든 정점 w do
if ( dist[u] + weight[u][w] < dist[w] )
then dist[w] <- dist[u] + weight[u][w]다익스트라 구현 코드:
class WGraphDijkstra : public WGraph {
int dist[MAX_VTXS]; // 시작노드로부터의 최단경로 거리
bool found[MAX_VTXS]; // 방문한 정점 표시 → 집합 S
public:
int chooseVertex() { // 가장 비용 적은 미방문 정점을 반환
int min = INF;
int minpos = -1;
for( int i=0 ; i<size ; i++ )
if( dist[i]< min && !found[i] ){
min = dist[i];
minpos = i;
}
return minpos;
}
void printDistance() { //모든 정점들의 dist[] 값 출력
for( int i=0 ; i<size ; i++)
printf("%5d", dist[i]);
printf("\n");
}
// Dijkstra의 최단 경로 알고리즘: start 정점에서 시작함.
void ShortestPath( int start ) {
for( int i=0 ; i<size ; i++) { //초기화: dist[], found[]
dist[i] = getEdge(start,i); //인접행렬 값 반환(간선 가중치)
found[i] = false; //처음에 S집합은 비어있음.
}
found[start] = true; // S에 포함
dist[start] = 0; // 최초 거리
for( int i=0 ; i<size ; i++ ){
printf("Step%2d:", i+1);
printDistance(); // 모든 dist[] 배열값 출력
int u = chooseVertex(); // S에 속하지 않은 비용 가장 작은 정점 반환
found[u] = true; // 집합 S에 포함
for( int w=0 ; w<size ; w++) {
if( found[w] == false )//S에 속하지 않는 노드 w의 dist값 갱신
if( dist[u] + getEdge(u,w) < dist[w] )
dist[w] = dist[u] + getEdge(u,w);
} // u를 거쳐가는 것이 최단 거리이면 dist[] 갱신
}
}
};관련 문제 풀이
1. 백준 1753 - 다익스트라 알고리즘 & 우선순위 큐 활용
#include <iostream>
#include <vector>
#include <queue>
#define INF 1000000 // 시작 노드에서 해당 노드까지의 경로가 없는 경우의 비용
#define MAX_VERTEX 20001 // 최대 vertex 개수
#define MAX_EDGE 300001 // 최대 edge 개수
using namespace std;
// 최소 비용 배열
int d[MAX_VERTEX];
// 간선 정보를 담은 Vector 생성
// index : 시작 노드
// value : pair<비용, 도착 노드> 목록
vector<pair<int, int> > edge[MAX_EDGE];
void dijkstra(int start_node){
// 시작 노드에서 시작 노드로 가는 비용은 0
d[start_node] = 0;
// 시작 노드부터 어떤 도착 노드까지의 최소 비용을 제시하는 간선 목록이며,
// pair<비용, 도착 노드> 형식의 우선 순위 큐이다.
priority_queue<pair<int, int> > pq;
// 시작 노드에서 시작 노드로 가는 경로와 비용을 pq 에 삽입
pq.push(make_pair(0, start_node));
// pq 의 모든 경로들을 확인할 때까지 반복
while(!pq.empty()){
// 기존의 우선 순위 큐는, 첫 번째 값을 기준으로 큰 값이 top 에 오도록 정렬되어있다.
// 하지만, 해당 알고리즘에선, 비용 값을 음수화 한 뒤 첫 번째 값으로 삽입하고, 도착 노드는 두 번째 값으로 삽입한다.
// 따라서, 비용이 가장 작은 값이 top 에 오도록 정렬되어있다.
// 즉, 가장 최소 비용을 주장하는 경로부터 확인하게 된다.
// 시작 노드에서 어떤 도착 노드까지의 최소 경로를 주장하는 pq 의 top 에서,
// 도착 노드를 현재 노드로 설정한다.
int current = pq.top().second;
// 시작 노드에서 현재 노드까지의 비용을 설정한다.
// 비용은 음수화되어있는 상태이므로, 양수화해서 사용한다.
int start_to_current_distance = -pq.top().first;
// 현재 경로는 확인 되었으므로, 우선 순위 큐에서 제거한다.
pq.pop();
// pq 의 top 에서 뽑은, 시작 노드부터 현재 노드까지의 비용과
// 최소 비용 배열에 있는, 시작 노드부터 현재 노드까지의 비용을 비교함으로써,
// pq 의 top 에서 뽑은, 시작 노드부터 현재 노드까지의 비용이 더 크면
// 굳이 해당 경로를 통해 인접한 노드들을 확인할 필요가 없으므로, 더 이상 확인하지 않음
if (d[current] < start_to_current_distance){
continue;
}
// 상단 조건문에 걸리지 않고 통과하면,
// 시작 노드부터 현재 노드까지는 최소 비용으로 이루어진 상태이므로,
// 이제 현재 노드와 연결된 노드들을 모두 검사한다.
for (int i=0; i<edge[current].size(); ++i){
// 다음 노드 설정
// 즉, 현재 노드와 i 번째로 인접한 노드
int next = edge[current][i].second;
// 시작 노드에서 다음 노드까지의 비용 설정
// 즉, 시작 노드에서 현재 노드까지의 비용 + 현재 노드에서 i 번째로 인접한 노드까지의 비용
int start_to_next_distance = start_to_current_distance + edge[current][i].first;
// 기존의, 시작 노드에서 다음 노드까지의 최소 비용보다
// 새롭게 계산한, 시작 노드에서 다음 노드까지의 비용이 더 작다면
// 최소 비용을 업데이트
if (d[next] > start_to_next_distance){
d[next] = start_to_next_distance;
// 이제, 갱신된 경로가 최소 비용임을 주장하기 위해
// 우선 순위 큐에 해당 경로 삽입
pq.push(make_pair(-start_to_next_distance, next));
}
}
}
}
int main(){
// 노드의 개수와 간선의 개수 입력
int v, e;
cin >> v >> e;
// 시작 노드 입력
int start_node;
cin >> start_node;
// 최소 비용 배열 초기화
for (int i=1; i<v+1; ++i){
d[i] = INF;
}
// 간선 저장
for (int i=0; i<e; ++i){
// 시작 노드, 도착 노드, 비용 입력
int start, end, cost;
cin >> start >> end >> cost;
// 시작 노드에 따른 <비용, 도착 노드> 저장
edge[start].push_back(make_pair(cost, end));
}
// 다익스트라 함수 실행
dijkstra(start_node);
// 최소 비용 배열 출력
for (int i=1; i<v+1; ++i){
if (d[i] == INF){
cout << "INF" << " ";
}
else{
cout << d[i] << " ";
}
}
return 0;
}
(참고: https://wooono.tistory.com/398)- 백준 1238 - 다익스트라 반복
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#define VMAX 1001
#define INF 987654321
using namespace std;
int n,e,target;
vector<pair<int,int>> a[VMAX];
int dist[VMAX];
int dijkstra(int start){
priority_queue<pair<int,int>> pq;
for(int i=0; i<VMAX; i++) dist[i]=INF;
pq.push({-0, start});
dist[start]=0;
while(!pq.empty()){
int x = pq.top().second;
int wx = -pq.top().first;
pq.pop();
for(int i=0; i<a[x].size(); i++){
int y = a[x][i].first;
int wy = a[x][i].second;
if(dist[y] > dist[x] + wy){
dist[y] = dist[x] + wy;
pq.push({-dist[y], y});
}
}
}
return -1;
}
int main(){
cin >> n >> e >> target;
int tdist[VMAX];
int result=0;
for(int x,y,w,i=0; i<e; i++){
scanf("%d %d %d", &x, &y, &w);
a[x].push_back({y,w});
}
dijkstra(target);
for(int i=1; i<=n; i++){
tdist[i] = dist[i];
}
for(int i=1; i<=n; i++){
if(i==target) continue;
dijkstra(i);
result = max(result, tdist[i] + dist[target]);
}
cout << result;
}
(참고: https://dmsvk01.tistory.com/110)