[python] 백준 1509 : 팰린드롬 분할

문제 링크
https://www.acmicpc.net/problem/1509

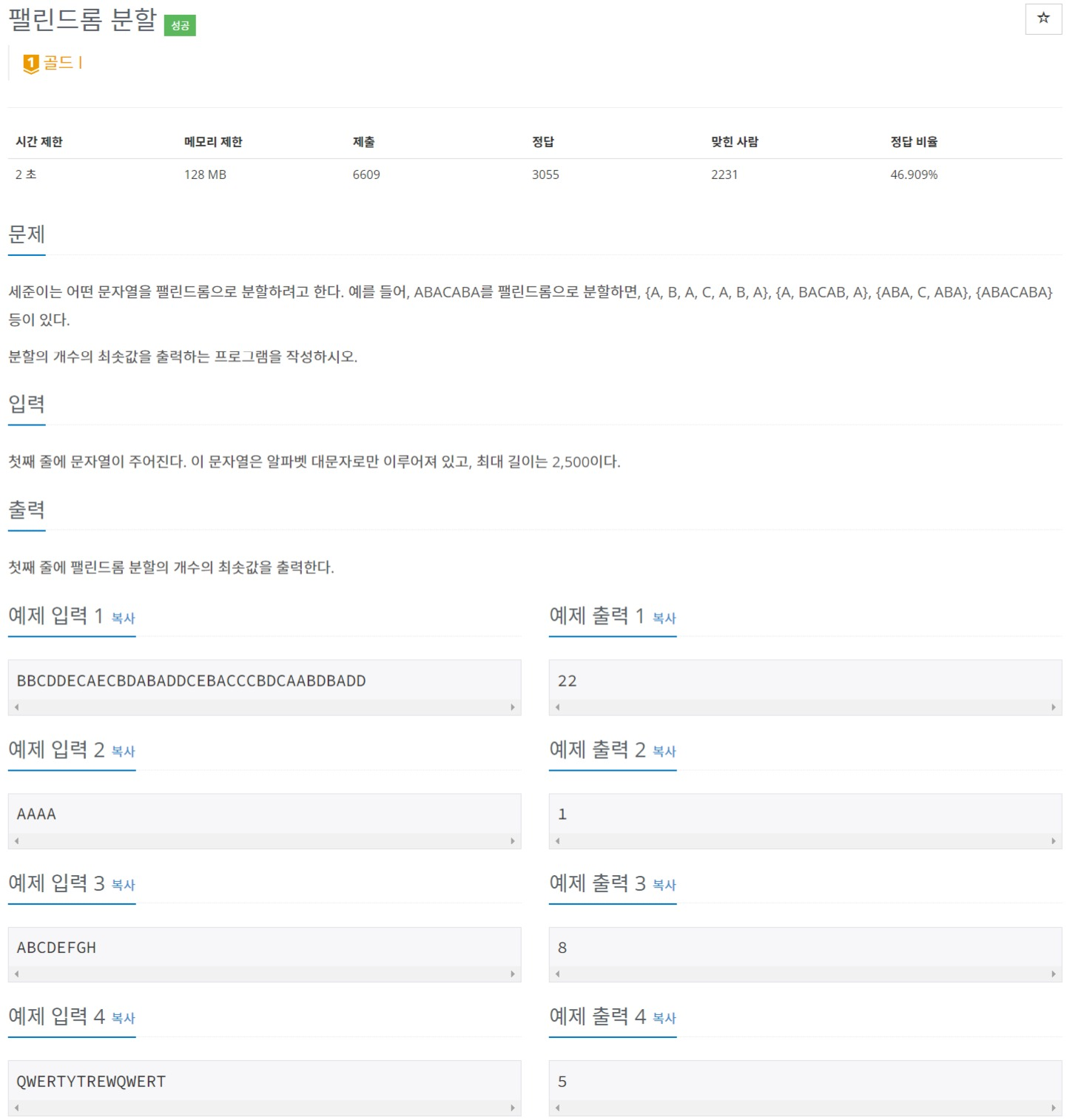
접근 1

첫 접근법은 브루트포스로 무식하게 다 탐색하였다.
key값이 시작 인덱스, value 값이 끝 인덱스들로 이루어진 리스트로 구성된 딕셔너리를 만든다. (ex. g = {0:[0,1,2], 1:[1,2]} 이런식으로...)
해당 팰린드롬 분할을 선택했을 때, 그 길이만큼 점프. 그 다음 것도 이와 같은 방식으로 마지막 인덱스까지 탐색하였다.
딩연히 시간초과

접근 2

이제 dp를 생각해보았다.
dp[i][j] = 인덱스 i~j 까지의 최소 팰린드롬 분할 수
점화식은 dp[i][j] = k(i~j)일 때 dp[i][k] + dp[k+1][j] 의 최솟값

그러나 O(N^3) 이 되어버려 2500^3 = 15625000000 번의 연산을 해야하는 상황이 되어버려 실패.

접근 3

결국 또다시 다른 사람들의 코드를 참고하였다.
https://yabmoons.tistory.com/592

is_p라는 리스트를 선언한다.
is_p[i][j]는 통해 i부터 j까지가 팰린드롬이면 1을 아니면 0을 반환

is_p = [[0 for j in range(L)] for i in range(L)]

길이가 1이나 2인 팰림드롬 분할을 미리 계산해준다.

for i in range(L):  # 길이 1 짜리 팰린드롬
    is_p[i][i] = 1

for i in range(1, L):  # 길이 2 짜리 펠린드롬 (AA, DD 같은 놈들)
    if s[i - 1] == s[i]:
        is_p[i - 1][i] = 1

이제 길이가 3 이상인 팰린드롬들을 구한다.
길이가 1 또는 2 인 팰린드롬을 구해놨기 때문에 3 이상부터 다 구할 수 있다.

중요한 부분은 처음과 끝이 같고, 그 사이가 팰린드롬이면 해당 구간 역시 팰린드롬이다.

for l in range(3, L + 1):  # 길이 3 ~ L 짜리 팰린드롬
    for start in range(L - l + 1):
        end = start + l - 1
        if s[start] == s[end] and is_p[start + 1][end - 1]:
            # 처음과 끝이 같고, 그 사이가 펠린드롬이면
            is_p[start][end] = 1  # start~end 도 팰린드롬

정답 코드

import sys

sys.setrecursionlimit(10 ** 8)
input = lambda: sys.stdin.readline().rstrip()

s = input()
L = len(s)


dp = [2500 for _ in range(L + 1)]
dp[-1] = 0
is_p = [[0 for j in range(L)] for i in range(L)]


for i in range(L):  # 길이 1 짜리 팰린드롬
    is_p[i][i] = 1

for i in range(1, L):  # 길이 2 짜리 팰린드롬 (AA, DD 같은 놈들)
    if s[i - 1] == s[i]:
        is_p[i - 1][i] = 1

for l in range(3, L + 1):  # 길이 3 ~ L 짜리 팰린드롬
    for start in range(L - l + 1):
        end = start + l - 1
        if s[start] == s[end] and is_p[start + 1][end - 1]:
            # 처음과 끝이 같고, 그 사이가 팰린드롬이면
            is_p[start][end] = 1  # start~end 도 팰린드롬

for end in range(L):
    for start in range(end + 1):
        if is_p[start][end]:
            dp[end] = min(dp[end], dp[start - 1] + 1)
        else:
            dp[end] = min(dp[end], dp[end - 1] + 1)

print(dp[L - 1])