[python] 백준 1647 : 도시 분할 계획

문제 링크
https://www.acmicpc.net/problem/1647

접근

문제는 크게 3가지 조건이 있다.

1. 마을은 2개로 분리
2. 마을 안에 임의의 두 집에 대해 경로 존재
3. 길 유지비의 합이 최소로 되게끔

사실 1번과 2번은 거의 같은 개념인데, 동떨어진 섬같은 집을 하나의 마을로 볼 수 없다는 것을 의미한다.

문제를 보고 유지비 c 가 적은 길부터 뽑으면 좋을 것 같다는 생각을 했다.
그렇기에 먼저 도로에 대한 정보를 유지비 c에 대하여 정렬한 후 차례대로 뽑는 것을 생각했다.
그 후 든 생각은 만일 이번에 뽑은 길이 이미 뽑았던 두 집에 대한 길이라면? 즉 사이클이 생기는 경우엔 어떻게 처리할 것인지에 대한 것이었다.

결국 각 집을 트리로 보고 이 트리를 합치는 것이라고 생각하면 문제는 쉽게 풀릴 것이라고 생각한다.
그리고 사이클이 생겨선 안되므로 Union-Find 알고리즘을 생각해보았다.

Union-Find

처음에 작성한 일반적인 Union-Find 알고리즘이다

def union(v1, v2):
    p1 = find(v1)
    p2 = find(v2)
    par[p2] = p1
    

def find(v):
    if v == par[v]:
        return v
    return find(par[v])  # 경로 압축

그러나 이 알고리즘으로는 최악의 경우 시간초과가 날 것이라고 생각했다.
만일 부모-자식 관계가 일자로 쭉 이어진 경우 최상단에 있는 root를 찾기 위해서는 O(N)의 시간복잡도가 걸린다.
각 도로마다 find 함수를 호출해야 하는데, 최대 도로의 개수 M = 100만 일 때 N * M 은 10만 * 100만으로 시간초과가 날 것이다.

( 이 경우 1의 root를 찾으려면 많이 거슬러 올라가야함...)

최적화된 Union-Find 알고리즘

https://gmlwjd9405.github.io/2018/08/31/algorithm-union-find.html
해당 글을 참고하였다.

find 연산 최적화

먼저 find 연산을 최적화 해보자.
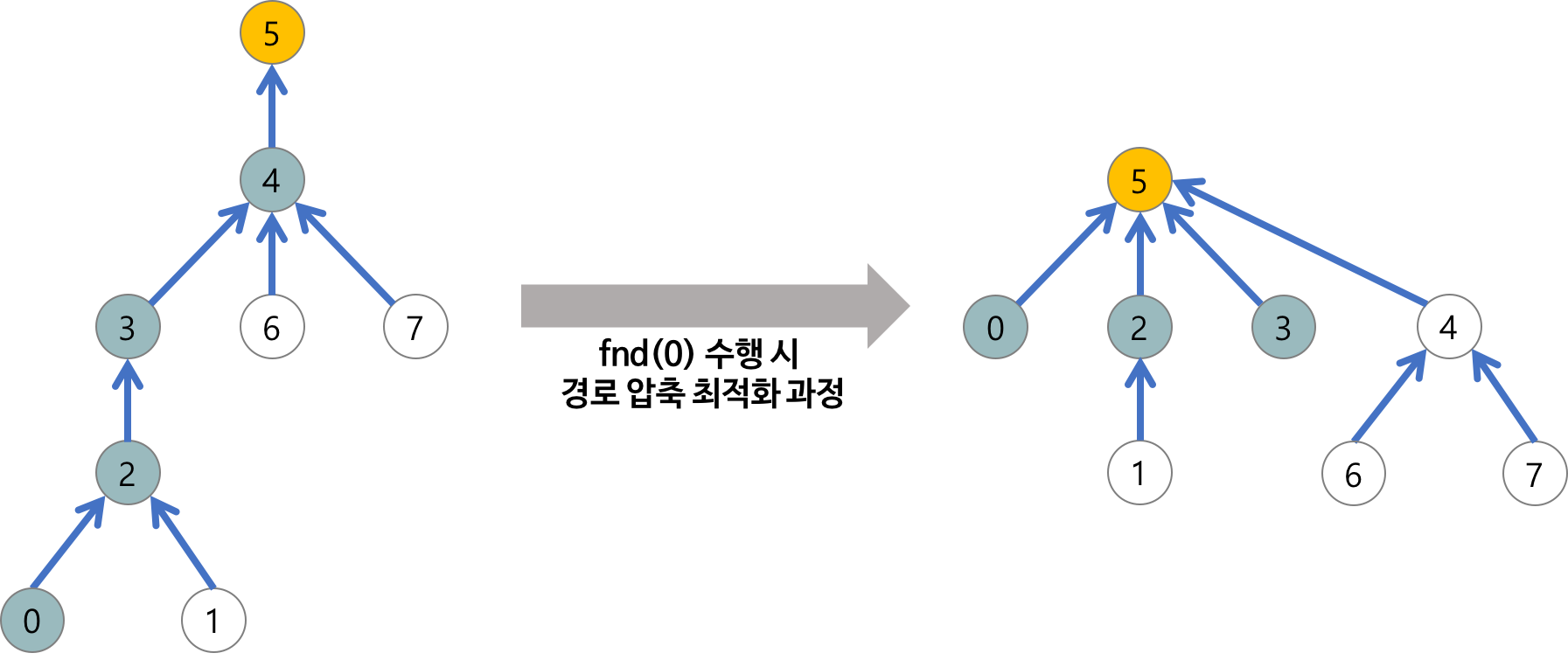
기존의 find 연산의 문제점은 자신의 부모(par)에게 밖에 가지 못한다는 것이다. 어차피 root가 같으면 같은 트리에 있다고 봐도 무방한데, 중간 다리들은 좀 뛰어넘고싶다.

최적화된 find 연산은 이처럼 중간 다리들을 뛰어 넘는 "경로 압축"의 역할을 해준다.

root = [i for i in range(n + 1)]

def find(v):
    if v == root[v]:
        return v
    root[v] = find(root[v])  # 경로 압축
    return root[v]

기존과 비슷하지만 root[v] = find(root[v]) 부분을 통해 지나왔던 모든 중간 다리들이 하나의 root를 가지게 된다. 이제 굳이 하나하나씩 올라갈 필요가 없어진 것이다!

union 연산 최적화

다음은 union 연산을 최적화해보자.
union 연산 최적화 개념의 핵심은 합칠 두 트리의 rank(높이로 봐도 무방)를 비교하는 것이다. 두 트리를 비교했을 때 rank가 더 높은 트리가 부모가 되는 것이다.
만일 두 트리의 rank가 같으면 아무나 부모가 되고, 부모가 된 트리는 rank+1 을 해준다.

rank = [0 for _ in range(n + 1)]

def union(v1, v2):
    r1 = find(v1)
    r2 = find(v2)

    if rank[r1] > rank[r2]:
        root[r2] = r1
    elif rank[r1] < rank[r2]:
        root[r1] = r2
    else:  # rank[r1] == rank[r2]
        root[r2] = r1
        rank[r1] += 1

정답 코드

import sys

sys.setrecursionlimit(10 ** 8)
input = lambda: sys.stdin.readline().rstrip()


def union(v1, v2):
    r1 = find(v1)
    r2 = find(v2)

    if rank[r1] > rank[r2]:
        root[r2] = r1
    elif rank[r1] < rank[r2]:
        root[r1] = r2
    else:  # rank[r1] == rank[r2]
        root[r2] = r1
        rank[r1] += 1


def find(v):
    if v == root[v]:
        return v
    root[v] = find(root[v])  # 경로 압축
    return root[v]


n, m = map(int, input().split())
roads = []
for _ in range(m):
    a, b, c = map(int, input().split())
    roads.append([a, b, c])
roads.sort(key=lambda x: x[2])

root = [i for i in range(n + 1)]
rank = [0 for _ in range(n + 1)]

c_sum = 0
div = n
for r in roads:
    if div == 2:
        break

    a, b, c = r[0], r[1], r[2]![](https://velog.velcdn.com/images%2Fsunkyuj%2Fpost%2F0d297976-522d-4cc6-a2b2-2dec6624d4d5%2Fimage.png)
    if find(a) == find(b):
        continue

    union(a, b)
    div -= 1
    c_sum += c

print(c_sum)
# print(root)