문제 링크
https://www.acmicpc.net/problem/1766
접근
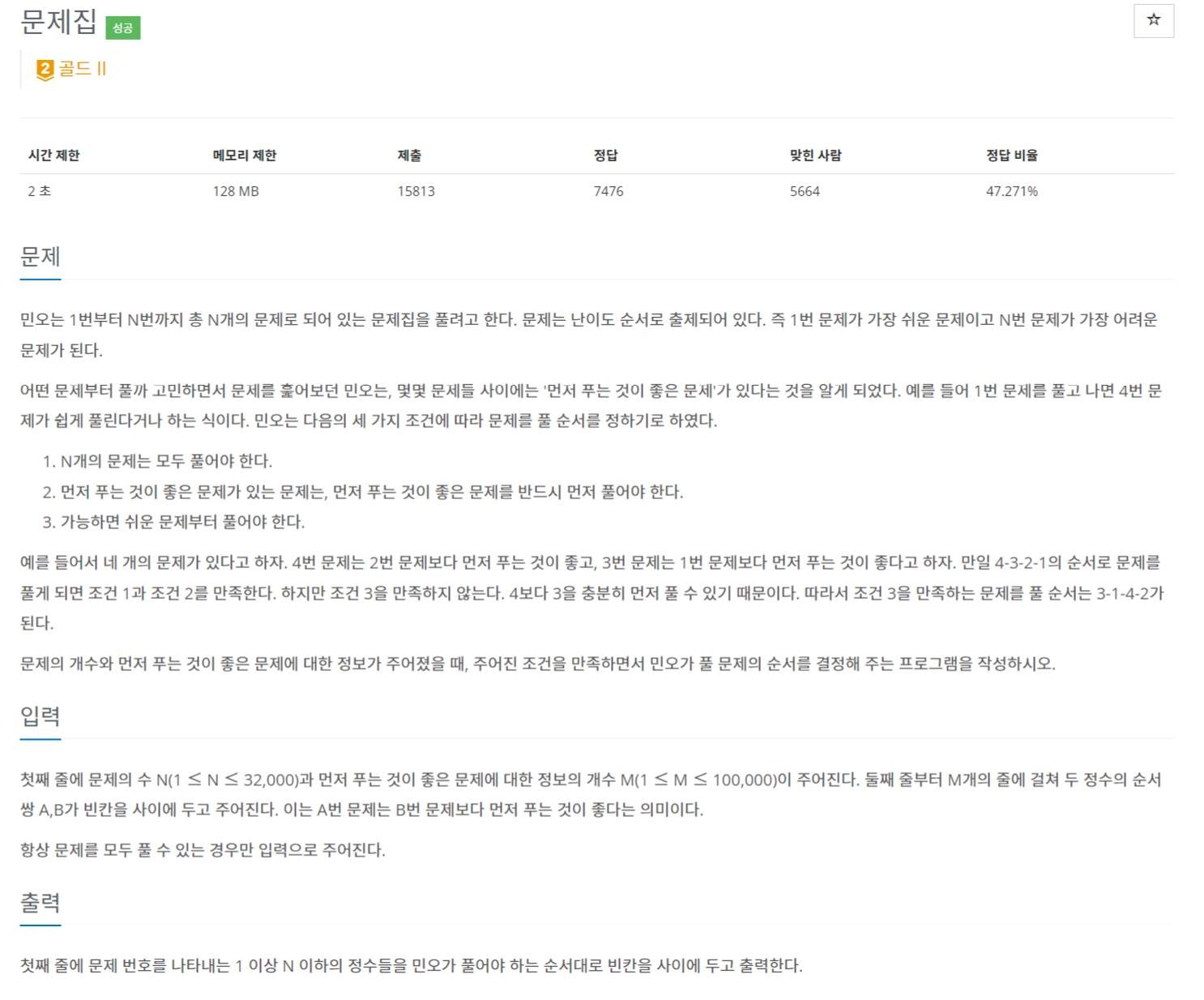
문제의 조건은 다음과 같다.
- N개의 문제는 모두 풀어야 한다.
- 먼저 푸는 것이 좋은 문제가 있는 문제는, 먼저 푸는 것이 좋은 문제를 반드시 먼저 풀어야 한다.
- 가능하면 쉬운 문제부터 풀어야 한다.
1번은 그냥 모든 문제를 다 풀어야된다는 것이므로 패스.
2번 조건과 3번 조건이 핵심인데, 문제에서 주어진 예제를 봐보자.
예를 들어서 네 개의 문제가 있다고 하자. 4번 문제는 2번 문제보다 먼저 푸는 것이 좋고, 3번 문제는 1번 문제보다 먼저 푸는 것이 좋다고 하자. 만일 4-3-2-1의 순서로 문제를 풀게 되면 조건 1과 조건 2를 만족한다. 하지만 조건 3을 만족하지 않는다. 4보다 3을 충분히 먼저 풀 수 있기 때문이다. 따라서 조건 3을 만족하는 문제를 풀 순서는 3-1-4-2가 된다.
즉, 4->2 그리고 3->1 과 같이 1,2번 문제는 선행되는 문제를 먼저 풀어야 하는 것이다. 따라서 위상정렬을 풀이로 생각해볼 수 있었다.
여기서 3번 조건이 추가가 되는데, 가능한 쉬운(숫자가 낮은) 문제부터 풀어야 한다는 것이다.
그래서 4-3-2-1은 안 되고 3-1-4-2는 되는 것이다.
이와 같은 조건을 고려하여 최소힙을 이용하여 풀이해보는 것을 떠올렸다.
풀이
n, m = map(int, input().split())
in_degree = [0 for _ in range(n + 1)] # in_degree[x] <-- x번 문제의 들어오는 차수
outs = {} # outs[a] = {b,c,d,...} <-- 문제 a 는 b,c,d,... 보다 먼저 풀어야한다.
for i in range(m):
a, b = map(int, input().split())
in_degree[b] += 1 # a->b 이므로 b의 in_degree를 하나 늘림
outs.setdefault(a, set()) # outs는 set을 value로 갖는 딕셔너리
outs[a].add(b) # a->b
각 문제들을 하나의 노드라고 생각하였다.
in_degree는 각 문제들의 들어오는 차수들을 저장해놓은 리스트이다.
outs는 노드(문제) a 가 가리키고 있는 노드들을 집합으로 묶은 딕셔너리이다.
outs= {a:set(b,c,d,...), x:set(y,z,...) }예를 들어 이와 같은 경우에서는, 문제 a는 b,c,d,...를 가리키고 있고, 문제 x는 y,z,...를 가리키고 있는 구조인 것이다.
다음은 본격적인 풀이를 위한 알고리즘이다.
minh = [] # 최소힙
for i in range(1, n + 1):
if in_degree[i] == 0:
heapq.heappush(minh, i) # 최소힙에 차수가 0인 문제들를 넣어줌
for i in range(n):
x = heapq.heappop(minh) # 문제 번호가 가장 낮은 문제를 pop
print(x, end=" ")
while x in outs and outs[x]: # 문제 x가 가리키고 있는 문제들만큼 반복
out = outs[x].pop() # 문제 x가 가리키고 있는 문제 하나 pop
in_degree[out] -= 1 # 해당 문제의 차수 하나 줄임
if in_degree[out] == 0: # 만약 그 문제의 차수가 0이 되면, 이제 풀 수 있게 되므로 최소힙에 집어넣음
heapq.heappush(minh, out)
먼저 heapq라이브러리를 이용하여 최소힙을 만들고, 차수가 0인 문제들을 최소힙에 넣어준다. 차수가 0 인 문제는 풀 수 있다는 문제이기 때문이다.
이제 최소힙에 있는 문제들을 총 n번 pop할 것인데, 항상 문제를 모두 풀 수 있는 경우만 입력으로 주어진다.고 하였으므로 위와 같이 반복문을 사용해도 무방하다.
문제 번호가 가장 낮은 문제(가장 쉬운 문제)를 pop해주어 해당 문제를 print한다(문제를 푼 것!) 그리고 방금 pop한 문제가 어떠한 문제들을 가리키고 있었다면, 가리키고 있던 문제들의 차수를 하나씩 빼주고, 만약 그 문제의 차수가 0이 되면, 이제 풀 수 있게 되므로 최소힙에 집어넣어 최소힙을 갱신한다.
위상정렬의 개념과 일치한다.
정답 코드
import sys
import heapq
sys.setrecursionlimit(10 ** 8)
input = lambda: sys.stdin.readline().rstrip()
n, m = map(int, input().split())
in_degree = [0 for _ in range(n + 1)] # in_degree[x] <-- x번 문제의 들어오는 차수
outs = {} # outs[a] = {b,c,d,...} <-- 문제 a 는 b,c,d,... 보다 먼저 풀어야한다.
for i in range(m):
a, b = map(int, input().split())
in_degree[b] += 1 # a->b 이므로 b의 in_degree를 하나 늘림
outs.setdefault(a, set()) # outs는 set을 value로 갖는 딕셔너리
outs[a].add(b) # a->b
minh = [] # 최소힙
for i in range(1, n + 1):
if in_degree[i] == 0:
heapq.heappush(minh, i) # 최소힙에 차수가 0인 문제들를 넣어줌
for i in range(n):
x = heapq.heappop(minh) # 차수가 가장 낮고 문제 번호도 가장 낮은 문제를 pop
print(x, end=" ")
while x in outs and outs[x]: # 문제 x가 가리키고 있는 문제들만큼 반복
out = outs[x].pop() # 문제 x가 가리키고 있는 문제 하나 pop
in_degree[out] -= 1 # 해당 문제의 차수 하나 줄임
if in_degree[out] == 0: # 만약 그 문제의 차수가 0이 되면, 이제 풀 수 있게 되므로 최소힙에 집어넣음
heapq.heappush(minh, out)