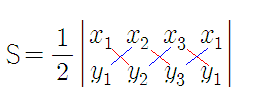문제 링크
https://www.acmicpc.net/problem/2162

https://www.youtube.com/watch?v=aVX5rOZuwjQ
https://darkpgmr.tistory.com/86
접근
N이 3000 정도로 O(N^2)도 거뜬하다고 판단하여 부담없이 코딩했다. 한 선에 대해서 다른 모든 선들을 다 확인하는 방식을 생각했다.
만일 교차가 되면 같은 그룹으로 묶고(Union) 아니면 그냥 안 묶고 넘어간다.
한가지 아쉬운 점은, 옛날에 분명 선분 교차를 판별하는 문제를 풀었는데 전혀 기억나지 않아 추가적으로 따로 알아본 것이다...
그래서 결론은, 이 문제에서 가장 중요한 것은 "선분 교차 판별"이라는 것이다.
선분 교차 판별
해당 블로그들을 참고했다.
https://jason9319.tistory.com/358
https://darkpgmr.tistory.com/86
선분이 교차되는 것을 판별하는 방법은 바로 "삼각형의 넓이"를 이용하는 것이다.
우선 다각형의 넓이를 구하는 공식을 보자.
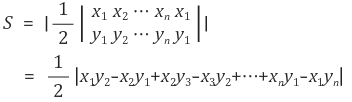
이렇다고 하는데... 벡터의 외적에 의해 저 식이 항상 성립한다고 한다.
저 식을 자세히 보면 한가지 규칙을 알 수 있는데, 고등학교때 종종 들었던 "신발끈 법칙(?)"이다.
[출처] https://mathworld.wolfram.com/PolygonArea.html
이렇게 크로스로 더해주고 빼주면, 그 다각형의 넓이가 나온다고 한다..!
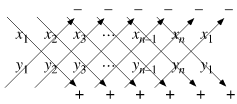
우리는 삼각형의 넓이를 원하니 구하고자 하는 삼각형의 넓이는 다음과 같을 것이다.
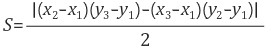
그럼 이거랑 선분이 교차하는 거랑 무슨 상관이냐고 할 수 있다.
우리는 넓이를 구할 때에는 항상 절대값을 사용한다. 자연스럽게 그냥 사용하지만 사실 수학에서의 부호는 방향이나 위치라고 볼 수 있다.
저 식에서 절대값을 빼면, 음수 또는 양수가 나올텐데
음수면 점 (x3,y3)이 (x1,y1)과(x2,y2)를 이은 선분 아래에,
양수면 점 (x3,y3)이 (x1,y1)과(x2,y2)를 이은 선분 위에 존재하게 된다.
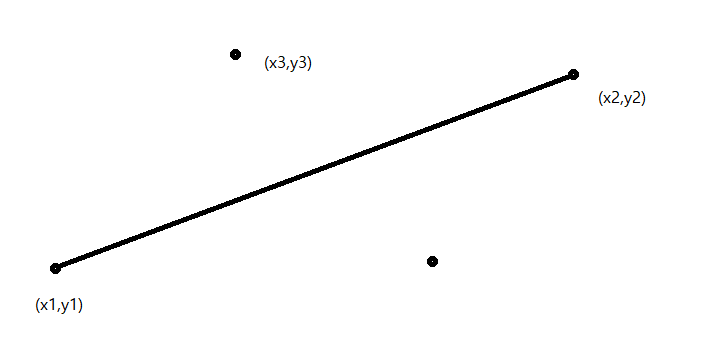
신발끈 공식을 기억하자
벡터의 외적을 이용한 방법도 있다. 나는 이 방법을 알고리즘에 사용했다.
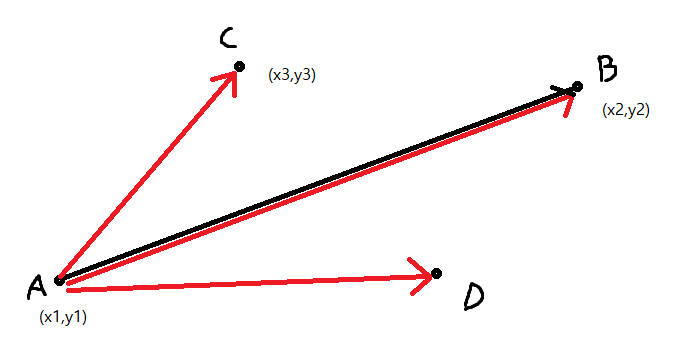
벡터AB와 벡터AC의 외적의 절대값은 삼각형 ABC의 넓이의 2배이다.
마찬가지로 절대값을 빼면 벡터의 상대적인 위치를 알 수 있다.
위 그림의 경우
벡터AB = (ab0,ab1)
벡터AC = (ac0,ac1) 이라고 하자
그렇다면 둘의 외적을 구하면 (이번에도 크로스!)
ab0*ac1 - ab1*ac0 의 값이 나온다.
이 값에 절대값을 씌우면 그냥 두 벡터의 평행사변형 넓이가 되지만,
씌우지 않으면 벡터AC가 벡터AB 위에 있는지 아래에 있는지 판별해주는 기능을 한다.
벡터 AD에 대해서도 같은 작업을 한다.
그리고 그 둘을 곱하여 양수가 나오면
그 둘이 같은 위치에 있으므로 교차하지 않고,
음수가 나오면 그 둘이 다른 위치에 있으므로 교차할 가능성이 있다.
예외 (네 점을 한 직선으로 이을 수 있는 경우)
교차할 가능성이 있다고 한 것은 이 경우 때문이다.
네 점이 한 직선 위에 있는 경우는

두 선분이 전혀 만나지 않는 경우와

두 선분이 겹쳐서 만나는 경우(혹은 한 선분이 완전히 포개지는 경우)가 있다.
어찌되었든 예외 처리를 잘 해주자.
그냥 각 점마다 서로 다른 선분 사이에 있는 점이 있는지 파악해주면 된다.
모든 점이 서로 다른 선분 위에 존재하는 경우가 없으면 첫번째 그림처럼 만나지 않는다.
그렇지 않으면, 특정 점이 다른 선분 위에 겹쳐져 있다는 것이므로, 두번째 그림처럼(은 아닐수도 있지만) 어쨋든 만난다.
풀이
cross(line1,line2) 함수
line1과 line2가 교차되어있는지 확인해주는 함수이다.
def cross(line1, line2):
a = (line1[0], line1[1]) # line 1
b = (line1[2], line1[3]) # line 1
c = (line2[0], line2[1]) # line 2
d = (line2[2], line2[3]) # line 2
if a > b:
a, b = b, a
if c > d:
c, d = d, c
ab = (b[0] - a[0], b[1] - a[1]) # a -> b
ac = (c[0] - a[0], c[1] - a[1]) # a -> c
ad = (d[2] - a[0], d[3] - a[1]) # a -> d
# 벡터로 삼각형 넓이 구하기
# 2S = ab_x * ac_y - ab_y * ac_x
t1 = ab[0] * ac[1] - ab[1] * ac[0] # 선분ab 와 점c로 만든 삼각형 넓이
t2 = ab[0] * ad[1] - ab[1] * ad[0] # 선분ab 와 점d로 만든 삼각형 넓이
if t1 * t2 <= 0:
if t1 == 0 and t2 == 0: # 한 직선 위에 네 점 있을 때
return a <= c <= b or a <= d <= b or c <= a <= d or c <= b <= d
return 1
else:
return 0먼저 점 a,b,c,d를 설정해준다.
이때, 편의상 무조건 a<=b 그리고 c<=d 가 되게끔 해준다.
다음은 벡터 ab와 ac 그리고 ad를 만들어준다.
아까 보았던 것 처럼 벡터의 각 성분을 크로스로 곱해주면 외적이 되는데, 두 벡터의 상대적 위치를 알 수 있다.
# 벡터로 삼각형 넓이 구하기
# 2S = ab_x * ac_y - ab_y * ac_x
t1 = ab[0] * ac[1] - ab[1] * ac[0] # 선분ab 와 점c로 만든 삼각형 넓이
t2 = ab[0] * ad[1] - ab[1] * ad[0] # 선분ab 와 점d로 만든 삼각형 넓이 문제에서 끝 점에 걸치는 것도 교차된 것이라 보므로 t1*t2 <= 0이면 교차 가능성이 높은 것이다.
만일 양수면 두 벡터 ac와 ad가 같은 영역에 있다는 것이므로 교차할 수 없다.(return 0)
마지막으로 네 점이 한 직선 위에 있는 경우 예외처리만 해주면 모든 경우를 다 나눌 수 있다.
전체 알고리즘
전체적인 알고리즘은 Union-Find 알고리즘을 이용하여 풀이했다.
for i in range(n - 1):
for j in range(i + 1, n):
if cross(lines[i], lines[j]) and cross(lines[j], lines[i]):
if find(i) != find(j):
union(i, j)모든 선분에 대하여 모든 선분과 교차하는지 본다.
만일 두 선분이 교차하고, 서로 다른 그룹이라면, 두 선분을 한 그룹으로 묶는다.
정답 코드
import sys
sys.setrecursionlimit(10 ** 8) # pypy 제출시 삭제!
input = lambda: sys.stdin.readline().rstrip()
# in_range = lambda y,x: 0<=y<n and 0<=x<m
def find(v):
if v == root[v]:
return v
root[v] = find(root[v])
return root[v]
def union(v1, v2):
r1 = find(v1)
r2 = find(v2)
if r1 > r2:
r1, r2 = r2, r1 # r1<=r2 되게끔
root[r2] = r1
def cross(line1, line2):
a = (line1[0], line1[1]) # line 1
b = (line1[2], line1[3]) # line 1
c = (line2[0], line2[1]) # line 2
d = (line2[2], line2[3]) # line 2
if a > b:
a, b = b, a
if c > d:
c, d = d, c
ab = (b[0] - a[0], b[1] - a[1]) # a -> b
ac = (c[0] - a[0], c[1] - a[1]) # a -> c
ad = (d[2] - a[0], d[3] - a[1]) # a -> d
# 벡터로 삼각형 넓이 구하기
# 2S = ab_x * ac_y - ab_y * ac_x
t1 = ab[0] * ac[1] - ab[1] * ac[0] # 선분ab 와 점c로 만든 삼각형 넓이
t2 = ab[0] * ad[1] - ab[1] * ad[0] # 선분ab 와 점d로 만든 삼각형 넓이
if t1 * t2 <= 0:
if t1 == 0 and t2 == 0: # 한 직선 위에 네 점 있을 때
return a <= c <= b or a <= d <= b or c <= a <= d or c <= b <= d
return 1
else:
return 0
n = int(input())
lines = [0 for _ in range(n)]
for i in range(n):
x1, y1, x2, y2 = map(int, input().split())
lines[i] = (x1, y1, x2, y2)
root = [i for i in range(n)]
for i in range(n - 1):
for j in range(i + 1, n):
if cross(lines[i], lines[j]) and cross(lines[j], lines[i]):
if find(i) != find(j):
union(i, j)
for i in range(n):
find(i)
print(len(set(root)))
root.sort()
cnt = 1
max_cnt = 1
for i in range(1, n):
cnt = cnt + 1 if root[i - 1] == root[i] else 1
max_cnt = max(max_cnt, cnt)
print(max_cnt)