문제 링크
https://www.acmicpc.net/problem/2357

접근
N과 M이 각각 10만이다.
만약 M개의 a,b 쌍의 탐색 범위가 모두 10만 가까이 된다고 치면
10만 * 10만으로 시간초과다!
즉, 무식한 방법으로는 풀 수 없다는 것이다.
연속된 구간에 대한 문제이므로 세그먼트 트리를 이용하여 문제를 풀 수 있다.
풀이
세그먼트 트리를 이용하여 특정 구간에서의 최솟값, 최댓값을 구해주면 쉽게 풀린다.
수열의 세그먼트 트리의 노드에 최솟값, 최댓값을 저장해놓고 비교하면 되는 것이다.
간단한 예를 들면, 5 1 2 3 4 라는 수열이 있다고 치고, 인덱스 0~3까지의 최솟값, 최댓값을 구하고자 한다.
5 1 2 3 의 최솟값, 최댓값은 각각 1,5 인데 이를 어떻게 구하는지 알아보자

우선 세그먼트 트리로 해당 수열을 나타내면 위와 같을 것이다.
우리는 세그먼트 트리의 각 노드에 "해당 구간의 최솟값,최댓값"을 저장할 것임을 다시한번 강조한다.
해당 트리에서 리프노드를 주목해보자.
세그먼트 트리에서 리프노드는 숫자 하나(혹은 한 영역)를 가리킨다.
숫자가 하나 뿐이라면 해당 구간(i~i)에서 최댓값과 최솟값 모두 그 숫자일 것이다.
그리고 이제 위로 올라가면서 왼쪽 자식에 있던 (좌)최대 (좌)최소와, 오른쪽 자식에 있던 (우)최대 (우)최소를 비교해가며,
현재 최댓값은 max((좌)최대 ,(우)최대 )
현재 최솟값은 min((좌)최소 ,(우)최소 ) 으로 갱신해준다.
이를 반복해서 원하는 값을 골라내면 되는 것이다.
다시 예시로 돌아와서...
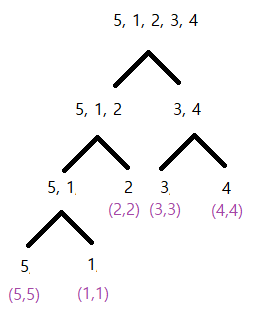
처음에 리프노드는 다음과 같은 상태일 것이다. (본인이 최대고 최소임)
그 다음 5,1 이 합쳐지는 곳을 보자.
해당 구간은 왼쪽 최대와 오른쪽 최대를 비교하여 더 큰 값을 최댓값으로 취한다.
최소도 마찬가지다.
따라서 5,1이 합쳐지는 곳의 최솟값과 최댓값은 (1,5)가 될 것이다.
이와 같은 방법으로 다음과 같은 세그먼트 트리를 얻을 수 있다.

정답 코드
import math
import sys
sys.setrecursionlimit(10 ** 8) # pypy 제출시 삭제!
input = lambda: sys.stdin.readline().rstrip()
# in_range = lambda y,x: 0<=y<n and 0<=x<m
def make_seg(idx, s, e):
if s == e:
seg[idx] = (arr[s], arr[s]) # min, max
return seg[idx]
mid = (s + e) // 2
l = make_seg(idx * 2, s, mid)
r = make_seg(idx * 2 + 1, mid + 1, e)
seg[idx] = (min(l[0], r[0]), max(l[1], r[1]))
return seg[idx]
def f(s, e, idx):
# 탐색범위 s~e
if e < a or b < s: # 범위 밖
return (1000000000, 0)
mid = (s + e) // 2
if a <= s and e <= b: # 탐색 범위가 작아서 다 리턴
return seg[idx]
else:
l = f(s, mid, idx * 2)
r = f(mid + 1, e, idx * 2 + 1)
return (min(l[0], r[0]), max(l[1], r[1]))
n, m = map(int, input().split())
arr = [int(input()) for _ in range(n)]
b = math.ceil(math.log2(n)) + 1
node_n = 1 << b
seg = [0 for _ in range(node_n)]
make_seg(1, 0, len(arr) - 1)
for _ in range(m):
a, b = map(int, input().split())
a, b = a - 1, b - 1 # idx
ans = f(0, len(arr) - 1, 1)
print(ans[0], ans[1])