[R] Dimension Reduction Methods

지금까지는 설명변수 $X_1,X_2,...X_p$를 사용하여 $y_i=\beta_0+\sum_{j=1}^p \beta_jx_{ij}+\epsilon_i$와 같은 모델을 정의했다.

이번에는 설명변수를 또 다른 변수로 변환한 다음, 변환한 변수를 사용하여 최소 제곱 모델을 적합하는 방법에 대해 알아보려고 한다. 이러한 방법을 차원 축소 방법 : Dimension Reduction Methods이라고 한다.

$Z_1,Z_2,...,Z_M$ ($M<p$)은 기존 설명변수의 선형결합으로, 다음과 같이 정의된다.

이때 상수 $\phi_{jm}$의 값이 적절하게 정해지면 최소제곱법을 이용하는 것보다 나은 성능을 보일 수 있다.
추정할 계수가 $p+1$개에서 $M+1$개로 줄어든다는 점에서 축소라는 말을 사용하는 것이다.

그럼 다음 식을 고려해보자.

위 식과 처음의 식을 결합하면 아래의 결과를 얻는다.

즉, $p$개의 $\beta_j$는 $M$개의 $\theta_m$의 합으로 표현되므로 편향이 생길 수 있지만, $M$보다 $p$가 충분히 크다면 분산을 크게 줄일 수 있어서 효과적이다!!

PCA : Principal Components Regression

PCA는 $n\times p$ 데이터 행렬 $X$의 차원을 줄이는 기법이다. 데이터의 첫 번째 주성분은 관측치가 가장 많이 변동하는 방향인데, 아래 그림에서 녹색 실선으로 표현되고 있다.

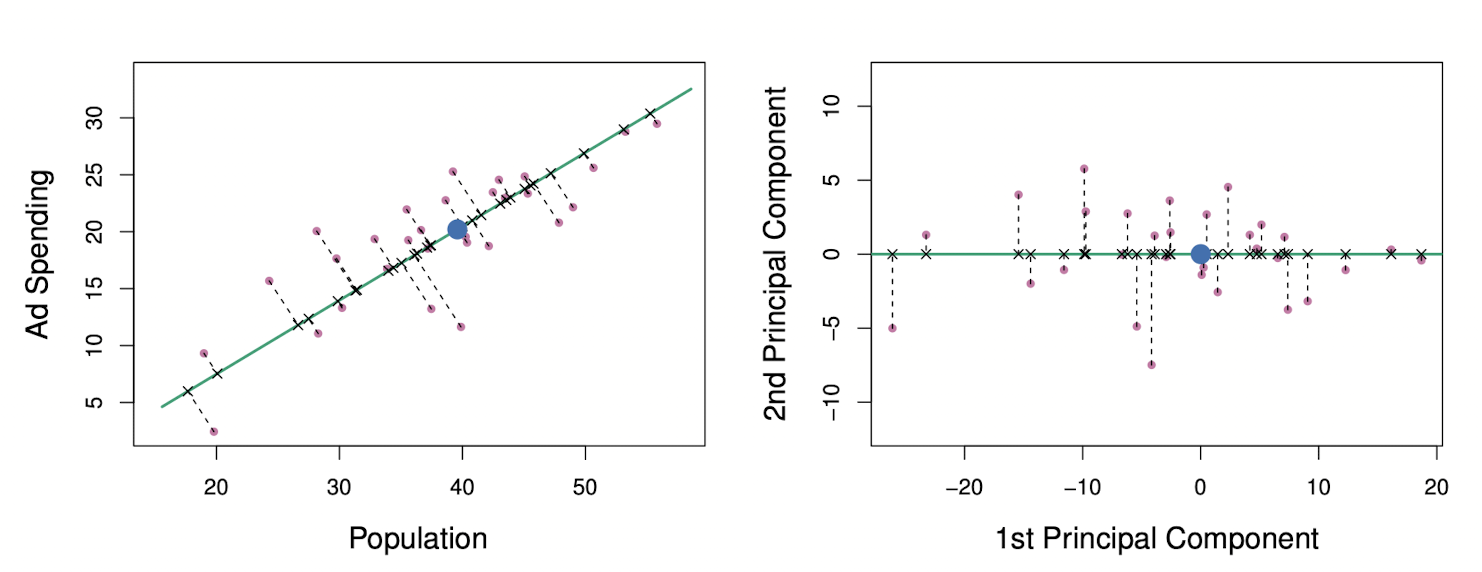
첫 번째 주성분을 수학적으로 표현하면

여기서 $\phi_{11} = 0.839$와 $\phi_{21} = 0.544$는 주성분 적재량으로, 위에서 언급한 방향을 정의한다.

PLS : Partial Least Squares

PCR : 주성분 회귀는 설명변수 $X_1,X_2,...,X_p$를 가장 잘 나타내는 선형 조합을 찾는 것이다. 이 방법은 비지도 학습 : Unsupervied way로 식별되며, 반응변수 $Y$가 주성분의 방향을 찾는데에 쓰이지 않는다.

PCR의 대안으로 PLS를 소개하겠다. PCR과 마찬가지로 차원축소 기법인데, 기존의 설명변수들의 선형 조합인 $Z_1,...,Z_M$을 새로운 방법으로 찾아낸다.

1st PLS direction을 계산한다면 우선 $p$개의 설명변수들을 표준화한 후, $\phi_{j1}$를 $Y$와 $X_j$간의 단순 선형 회귀 계수로 설정하여 1st direction $Z_1$을 계산한다. 이때 $\phi_{j1}$는 $Y$와 $X_j$간의 상관관계에 비례한다. 반응변수와 높은 상관관계를 갖는 변수에 높은 가중치를 부여하게 되는 것이다.

일반적으로 PLS를 수행하기 전에 반응변수와 설명변수를 표준화한다.

Training / Test로 분할한 데이터셋에 대해 PCR을 수행해보자.

> library(pls)
> set.seed(2)
> pcr.fit = pcr(Salary ~ ., data=Hitters, subset = train, scale = TRUE, validation = 'CV')
> summary(pcr.fit)
Data: 	X dimension: 131 19 
	Y dimension: 131 1
Fit method: svdpc
Number of components considered: 19

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept)  1 comps  2 comps  3 comps  4 comps  5 comps  6 comps  7 comps  8 comps  9 comps  10 comps  11 comps
CV           428.3    327.3    329.9    324.4    325.3    325.6    326.3    328.3    323.9    322.7     322.9     323.6
adjCV        428.3    326.9    329.3    323.5    324.4    324.3    325.0    327.0    322.6    320.8     321.3     322.0
       12 comps  13 comps  14 comps  15 comps  16 comps  17 comps  18 comps  19 comps
CV        328.4     329.1     335.4     337.9     332.2     337.5     343.2     342.7
adjCV     326.5     327.0     333.0     335.3     329.6     334.5     339.9     338.9

TRAINING: % variance explained
        1 comps  2 comps  3 comps  4 comps  5 comps  6 comps  7 comps  8 comps  9 comps  10 comps  11 comps  12 comps
X         39.32    61.57    71.96    80.83    85.95    89.99    93.25    95.34    96.55     97.61     98.28     98.85
Salary    43.87    43.93    47.36    47.37    49.52    49.55    49.63    50.98    53.00     53.00     53.02     53.05
        13 comps  14 comps  15 comps  16 comps  17 comps  18 comps  19 comps
X          99.22     99.53     99.79     99.91     99.97     99.99    100.00
Salary     53.80     53.85     54.03     55.85     55.89     56.21     58.62
> validationplot(pcr.fit, val.type = 'MSEP')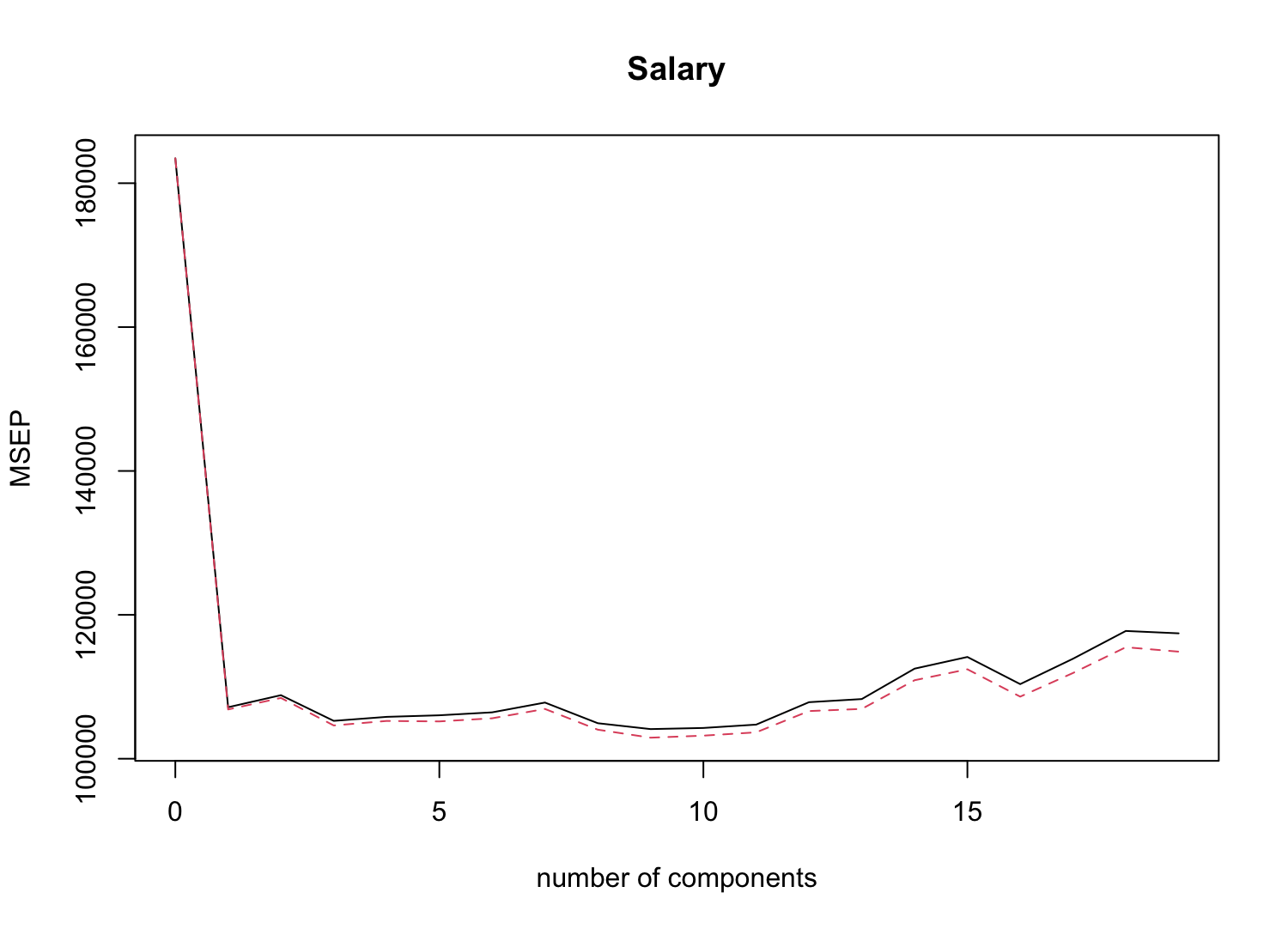

MSEP가 $M=5$에서 가장 작으므로, 5개의 주성분을 사용할 때의 Test MSE를 계산해보자.

> yhat = predict(pcr.fit, x[test,], ncomp = 5)
> mean((y[test]-yhat)^2)
[1] 142811.8

이제 전체 데이터 셋에서 5개의 주성분을 사용하는 모델을 적합해보자.

> pcr.fit = pcr(y ~ x, scale = TRUE, ncomp = 5)
> summary(pcr.fit)
Data: 	X dimension: 263 19 
	Y dimension: 263 1
Fit method: svdpc
Number of components considered: 5
TRAINING: % variance explained
   1 comps  2 comps  3 comps  4 comps  5 comps
X    38.31    60.16    70.84    79.03    84.29
y    40.63    41.58    42.17    43.22    44.90

마찬가지로 교차검증으로 PLS의 MSEP를 확인해보자.

> pls.fit = plsr(Salary ~ ., data=Hitters, subset = train, scale = TRUE, validation = 'CV')
> summary(pls.fit)
Data: 	X dimension: 131 19 
	Y dimension: 131 1
Fit method: kernelpls
Number of components considered: 19

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept)  1 comps  2 comps  3 comps  4 comps  5 comps  6 comps  7 comps  8 comps  9 comps  10 comps  11 comps
CV           428.3    323.4    326.5    324.3    331.2    333.5    340.6    340.9    350.2    351.1     348.1     344.8
adjCV        428.3    323.0    325.0    323.1    329.5    331.2    337.1    337.9    346.3    347.3     344.7     341.5
       12 comps  13 comps  14 comps  15 comps  16 comps  17 comps  18 comps  19 comps
CV        350.5     356.1     359.3     360.4     357.8     350.0     349.5     349.9
adjCV     346.7     350.8     354.4     355.4     353.2     345.9     345.5     345.8

TRAINING: % variance explained
        1 comps  2 comps  3 comps  4 comps  5 comps  6 comps  7 comps  8 comps  9 comps  10 comps  11 comps  12 comps
X         39.13    48.80    60.09    75.07    78.58    81.12    88.21    90.71    93.17     96.05     97.08     97.61
Salary    46.36    50.72    52.23    53.03    54.07    54.77    55.05    55.66    55.95     56.12     56.47     56.68
        13 comps  14 comps  15 comps  16 comps  17 comps  18 comps  19 comps
X          97.97     98.70     99.12     99.61     99.70     99.95    100.00
Salary     57.37     57.76     58.08     58.17     58.49     58.56     58.62
> validationplot(pls.fit, val.type = 'MSEP')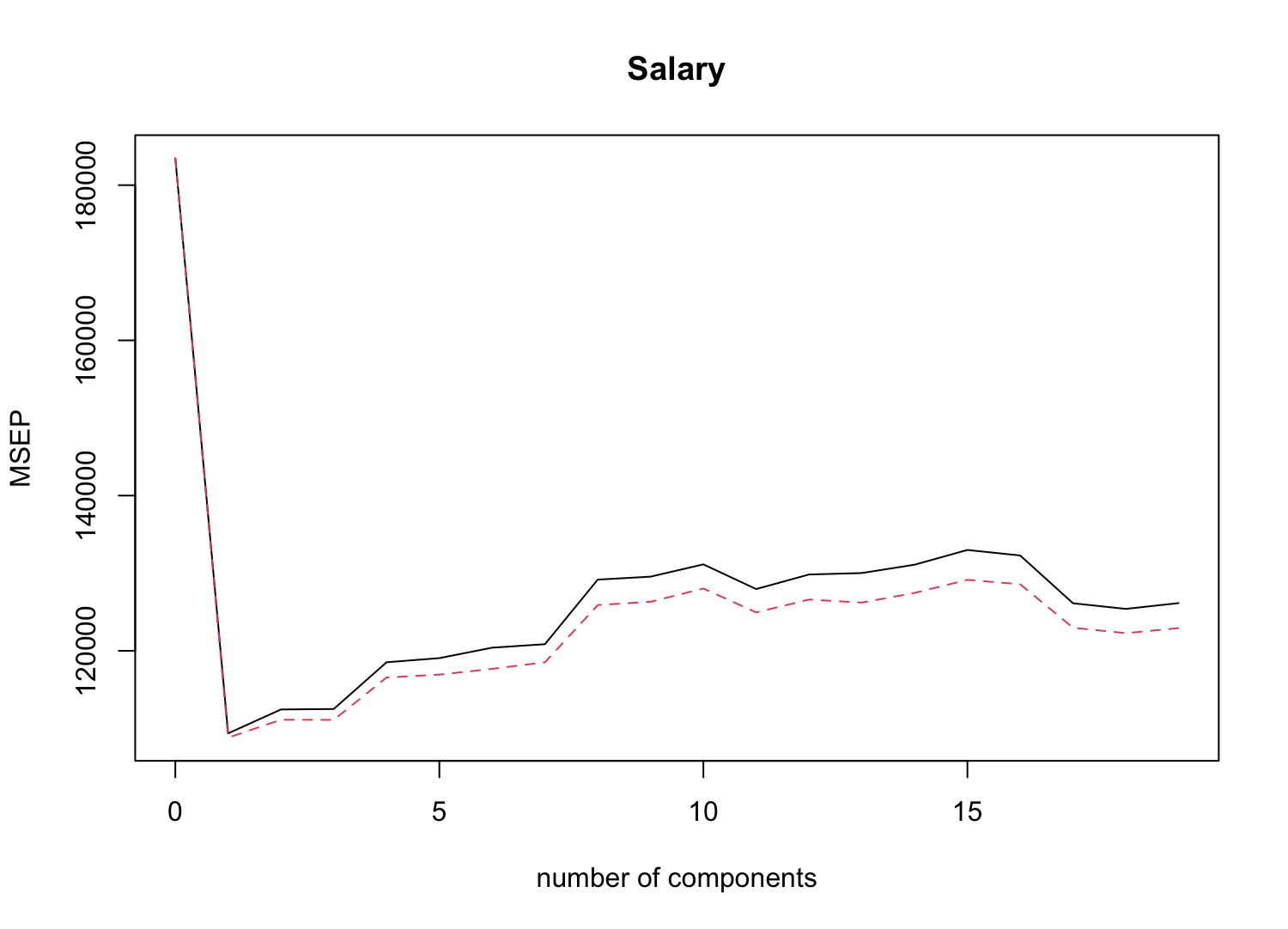

MSEP가 $M=2$일 때 가장 작으므로, 2개의 PLS direction만 사용할 때의 Test MSE를 계산해보자.

> yhat = predict(pls.fit, x[test,], ncomp = 2)
> mean((y[test]-yhat)^2)
[1] 145367.7
> yhat = predict(pls.fit, x[test,], ncomp = 2)
> mean((y[test]-yhat)^2)
[1] 118381.7

마지막으로, 전체 데이터셋에 대해 2개의 PLS direction만 사용하는 모델을 적합하자.

> pls.fit = plsr(y ~ x, scale = TRUE, ncomp = 2)
> summary(pls.fit)
Data: 	X dimension: 263 19 
	Y dimension: 263 1
Fit method: kernelpls
Number of components considered: 2
TRAINING: % variance explained
   1 comps  2 comps
X    38.08    51.03
y    43.05    46.40