[R] Shrinkage Methods

sunnyboy·2024년 10월 23일

R Regression

Data Mining

목록 보기

8/9

바로 이전 포스트에서 언급했듯이, 모델 적합시에 모든 설명변수 $p$ 개를 사용하면서
계수 추정치를 적절히 제한하는 방식으로 성능 개선이 가능하다.

이것은 계수 추정치를 0에 가깝게 수축하는 것과 같은 방식이다. 그럼 Shrinkage하는 방법으로는 어떤 것들이 있을까?

가장 잘 알려진 두 가지 기법인 Ridge Regression과 Lasso에 대해 알아보자.

Ridge Regression

Ridge Regression으로 추정한 계수를 $\hat\beta^R$ 이라고 하자. 이때 $\hat\beta^R$ 을 다음과 같이 정의한다.

\hat\beta^R=argmin_\beta\left[\sum_{i=1}^n (y_i-\beta_0-\sum_{j=1}^p\beta_jx_{ij})^2 + \lambda\sum_{j=1}^p \beta_j^2\right]

Ridge 추정량의 형태는 LSE 추정량에 $\beta_j$ 의 제곱합이 패널티로 더해진 꼴이다. 따라서 전체적으로 $\beta_j$ 를 수축시키는 효과가 발생한다.(intercept 항인 $\beta_0$ 제외)

Tuning parameter $\lambda$ 가 0일 때는 Least squares estimate와 같지만, $\lambda \rightarrow\infty$ 에 따라 Coefficient는 0으로 수렴하게 된다. 이때 $\lambda$ 는 K-fold CV로 결정한다.

LSE는 설명변수의 Scale에 영향을 받지 않지만, Ridge Coefficient는 패널티 때문에 설명변수의 Scale에 크게 의존한다. 따라서 모형을 적합하기 전에 설명변수를 Standardization할 필요가 있다.

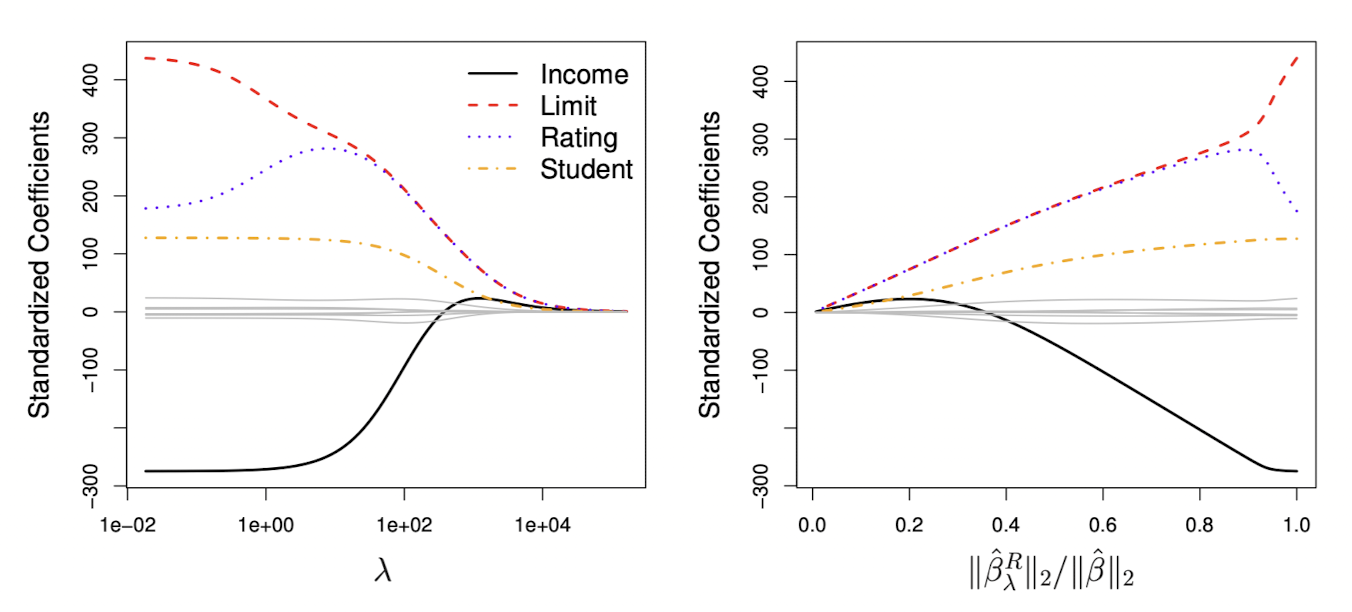
왼쪽의 그림은 Credit 데이터셋의 변수 Income, Limit, Rating, Student 각각에서 $\lambda$ 에 따른 릿지 계수 추정값을 나타낸 그래프다. 일반적으로 Ridge Coefficient Estimate는 $\lambda$ 가 증가함에 따라 0으로 수렴한다.

오른쪽은 x축이 $||\hat\beta_\lambda^R||_2/||\hat\beta||_2$ 으로, $\lambda=0$ 일 때 0, $\lambda=\infty$ 일 때 1의 값을 갖는다. 따라서 Ridge Coefficient Estimate가 0으로 얼마나 수축되었나를 나타내는 지표이다.

이제 glmnet 패키지를 이용하여 Ridge를 적합해볼건데, 우선 데이터 결측값을 제거하자.

> library(glmnet)
> library(ISLR)
> head(Hitters)
                  AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits CHmRun CRuns CRBI CWalks League Division PutOuts
-Andy Allanson      293   66     1   30  29    14     1    293    66      1    30   29     14      A        E     446
-Alan Ashby         315   81     7   24  38    39    14   3449   835     69   321  414    375      N        W     632
-Alvin Davis        479  130    18   66  72    76     3   1624   457     63   224  266    263      A        W     880
-Andre Dawson       496  141    20   65  78    37    11   5628  1575    225   828  838    354      N        E     200
-Andres Galarraga   321   87    10   39  42    30     2    396   101     12    48   46     33      N        E     805
-Alfredo Griffin    594  169     4   74  51    35    11   4408  1133     19   501  336    194      A        W     282
                  Assists Errors Salary NewLeague
-Andy Allanson         33     20     NA         A
-Alan Ashby            43     10  475.0         N
-Alvin Davis           82     14  480.0         A
-Andre Dawson          11      3  500.0         N
-Andres Galarraga      40      4   91.5         N
-Alfredo Griffin      421     25  750.0         A
> str(Hitters)
'data.frame':	322 obs. of  20 variables:
 $ AtBat    : int  293 315 479 496 321 594 185 298 323 401 ...
 $ Hits     : int  66 81 130 141 87 169 37 73 81 92 ...
 $ HmRun    : int  1 7 18 20 10 4 1 0 6 17 ...
 $ Runs     : int  30 24 66 65 39 74 23 24 26 49 ...
 $ RBI      : int  29 38 72 78 42 51 8 24 32 66 ...
 $ Walks    : int  14 39 76 37 30 35 21 7 8 65 ...
 $ Years    : int  1 14 3 11 2 11 2 3 2 13 ...
 $ CAtBat   : int  293 3449 1624 5628 396 4408 214 509 341 5206 ...
 $ CHits    : int  66 835 457 1575 101 1133 42 108 86 1332 ...
 $ CHmRun   : int  1 69 63 225 12 19 1 0 6 253 ...
 $ CRuns    : int  30 321 224 828 48 501 30 41 32 784 ...
 $ CRBI     : int  29 414 266 838 46 336 9 37 34 890 ...
 $ CWalks   : int  14 375 263 354 33 194 24 12 8 866 ...
 $ League   : Factor w/ 2 levels "A","N": 1 2 1 2 2 1 2 1 2 1 ...
 $ Division : Factor w/ 2 levels "E","W": 1 2 2 1 1 2 1 2 2 1 ...
 $ PutOuts  : int  446 632 880 200 805 282 76 121 143 0 ...
 $ Assists  : int  33 43 82 11 40 421 127 283 290 0 ...
 $ Errors   : int  20 10 14 3 4 25 7 9 19 0 ...
 $ Salary   : num  NA 475 480 500 91.5 750 70 100 75 1100 ...
 $ NewLeague: Factor w/ 2 levels "A","N": 1 2 1 2 2 1 1 1 2 1 ...
> sum(is.na(Hitters))
[1] 59

데이터셋을 Training Set과 Test Set으로 나눈 다음 $\lambda=10^{10}$ 부터 $\lambda=10^{-2}$ 내의 $\lambda$ 에서 모델을 적합시켜보자.

> dim(Hitters)
[1] 263  20
> x = model.matrix(Salary ~., Hitters)[,-1];
> y = Hitters$Salary; length(y)
[1] 263
> set.seed(1)
> train = sort(sample(1:nrow(x), nrow(x)/2))
> test = setdiff(1:nrow(x), train)
> y.test = y[test]
> ridge.mod = glmnet(x[train,], y[train], alpha = 0, lambda = grid, thresh = 1e-12)
> ridge.pred = predict(ridge.mod, s = 4, newx = x[test,])
> mean((ridge.pred - y.test)^2)
[1] 142199.2

적합된 모델에서 임의로 $\lambda=4$ 일 때의 MSE를 구해보니 약 142,199라는 값이 나왔다. 다음으로 $\lambda=10^{10}$ 으로 큰 값의 MSE를 구해보겠다.

> ridge.pred = predict(ridge.mod, s = 1e10, newx = x[test,])
> mean((ridge.pred - y.test)^2)
[1] 224669.8

$\lambda=0$ 인 LSE를 구해보면

> ridge.pred = predict(ridge.mod, s = 0, newx = x[test,], exact = T, x=x[train,], y=y[train])
> mean((ridge.pred - y.test)^2)
[1] 168588.6

이번에는 K-fold CV로 최적의 $\lambda$ 를 찾아보자.

> cv.out = cv.glmnet(x[train, ], y[train], alpha = 0, nfold = 10)
> plot(cv.out)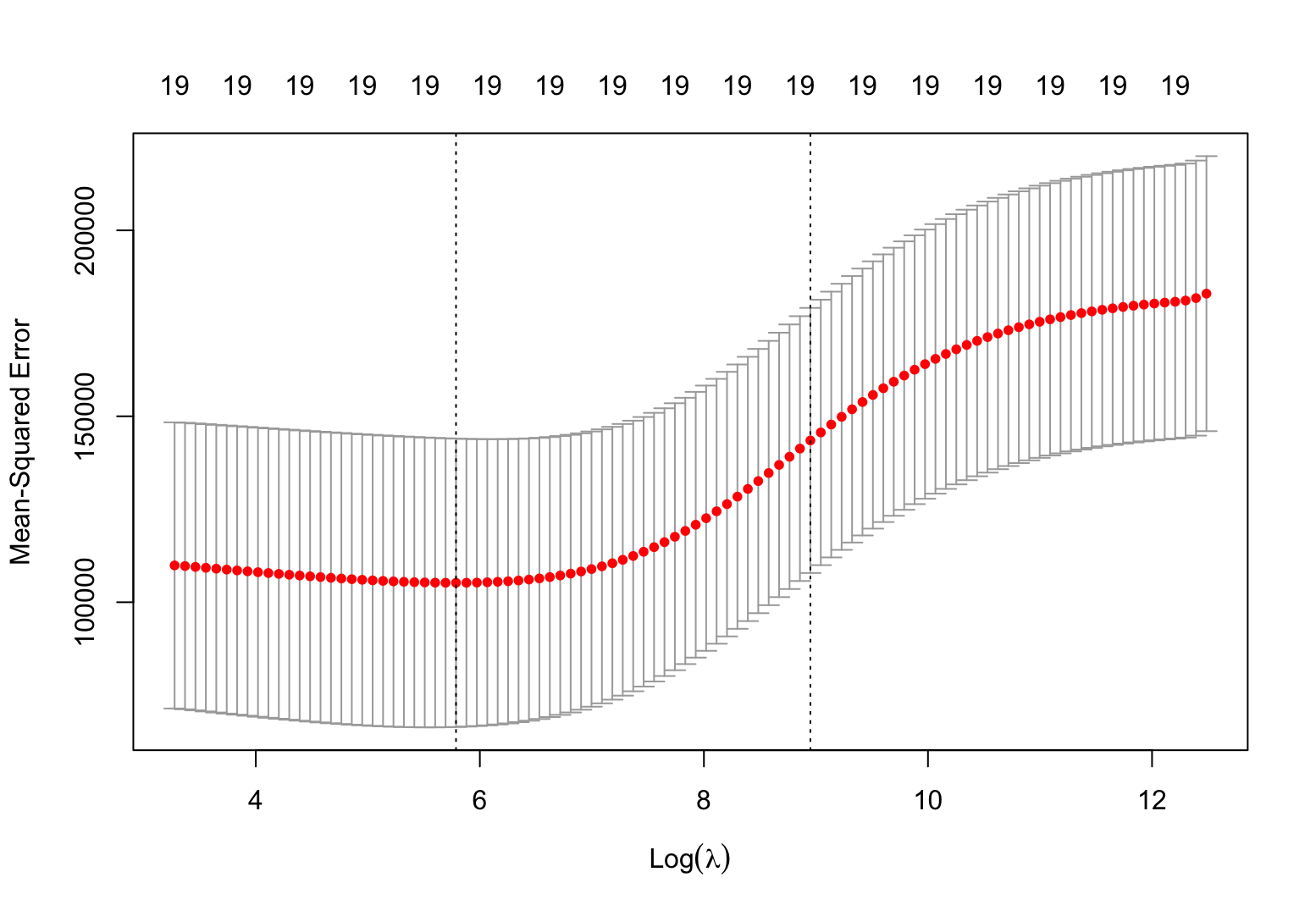

> bestlam = cv.out$lambda.min; bestlam
[1] 326.0828
> yhat = predict(ridge.mod, newx = x[test, ], s = bestlam)
> mean((y[test] - yhat)^2) # MSE of test data
[1] 139856.6

best lambda는 326.0828로, MSE는 139856.6으로 앞서 $\lambda=4$ 에서 계산한 MSE보다 좋은 성능을 보인다.

> out = glmnet(x, y, alpha = 0)
> predict(out, type = "coefficient", s = bestlam)[1:20,]
 (Intercept)        AtBat         Hits        HmRun         Runs          RBI        Walks        Years       CAtBat        CHits       CHmRun 
 15.44383120   0.07715547   0.85911582   0.60103106   1.06369007   0.87936105   1.62444617   1.35254778   0.01134999   0.05746654   0.40680157 
       CRuns         CRBI       CWalks      LeagueN    DivisionW      PutOuts      Assists       Errors   NewLeagueN 
  0.11456224   0.12116504   0.05299202  22.09143197 -79.04032656   0.16619903   0.02941950  -1.36092945   9.12487765

K-fold CV를 이용해 선택한 $\lambda$ 로 전체 데이터셋에서 모델을 다시 적합하고, 계수 추정치를 확인해보니 예상대로 0인 값은 없었다.

Lasso

Lasso coefficient estimate가 $\hat\beta^L$ 라고 할때, 다음과 같이 정의한다.

\hat\beta^L=argmin_\beta\left[\sum_{i=1}^n (y_i-\beta_0-\sum_{j=1}^p\beta_jx_{ij})^2 + \lambda\sum_{j=1}^p |\beta_j|\right]

Ridge Regression은 $\beta_j$ 를 수축시키지만 정확히 0으로 만들 수는 없다. 하지만 Lasso는 $\beta_j$ 를 0으로 만들 수 있다는 장점이 있다.

Tuning parameter $\lambda$ 가 0일 때 Lasso Coefficient는 Least squares estimate와 같지만, $\lambda$ 가 충분히 크면 모든 Coefficient가 0인 null model이 된다. 마찬가지로 $\lambda$ 는 K-fold CV로 결정한다.

Lasso도 모델 적합 전에 설명변수를 Standardization할 필요가 있다.

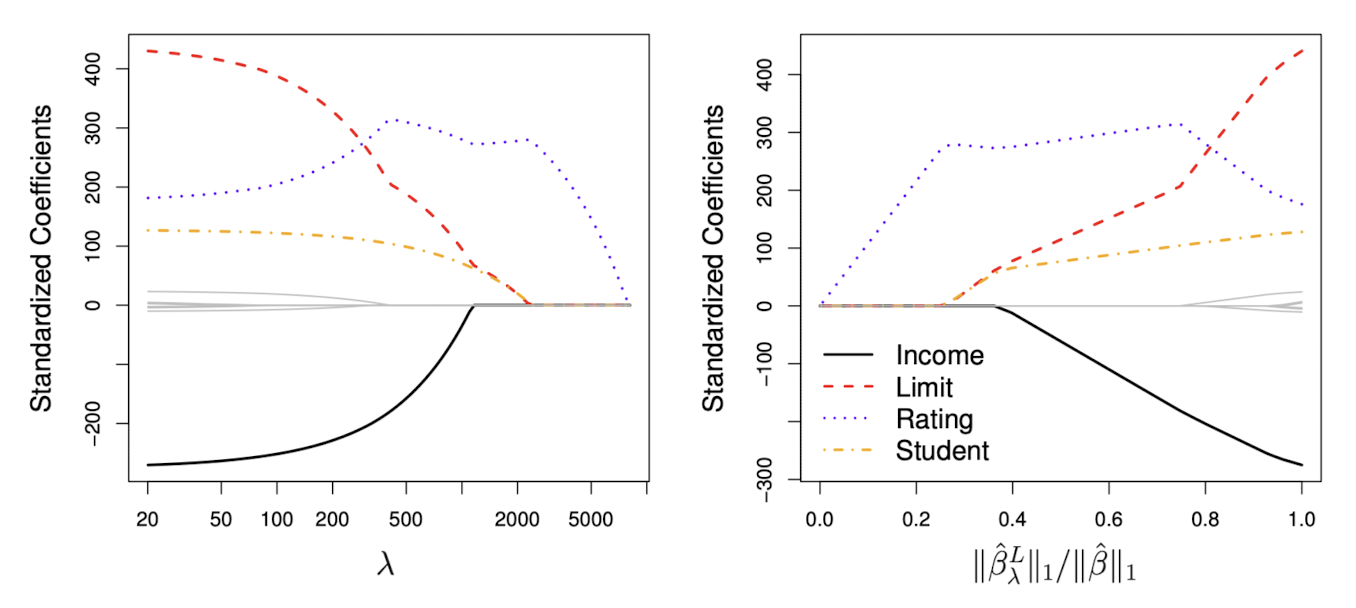
왼쪽의 그래프를 보면 Ridge랑은 다르게 $\lambda$ 가 충분히 커졌을 때 Coefficient가 0이 된다. 또한 오른쪽 그래프에서도 비슷한 결과를 볼 수 있다.

> lasso.mod = glmnet(x[train,], y[train], alpha = 1, lambda = grid)
> set.seed(1)
> cv.out = cv.glmnet(x[train, ], y[train], alpha = 1, nfold = 10)
> plot(cv.out)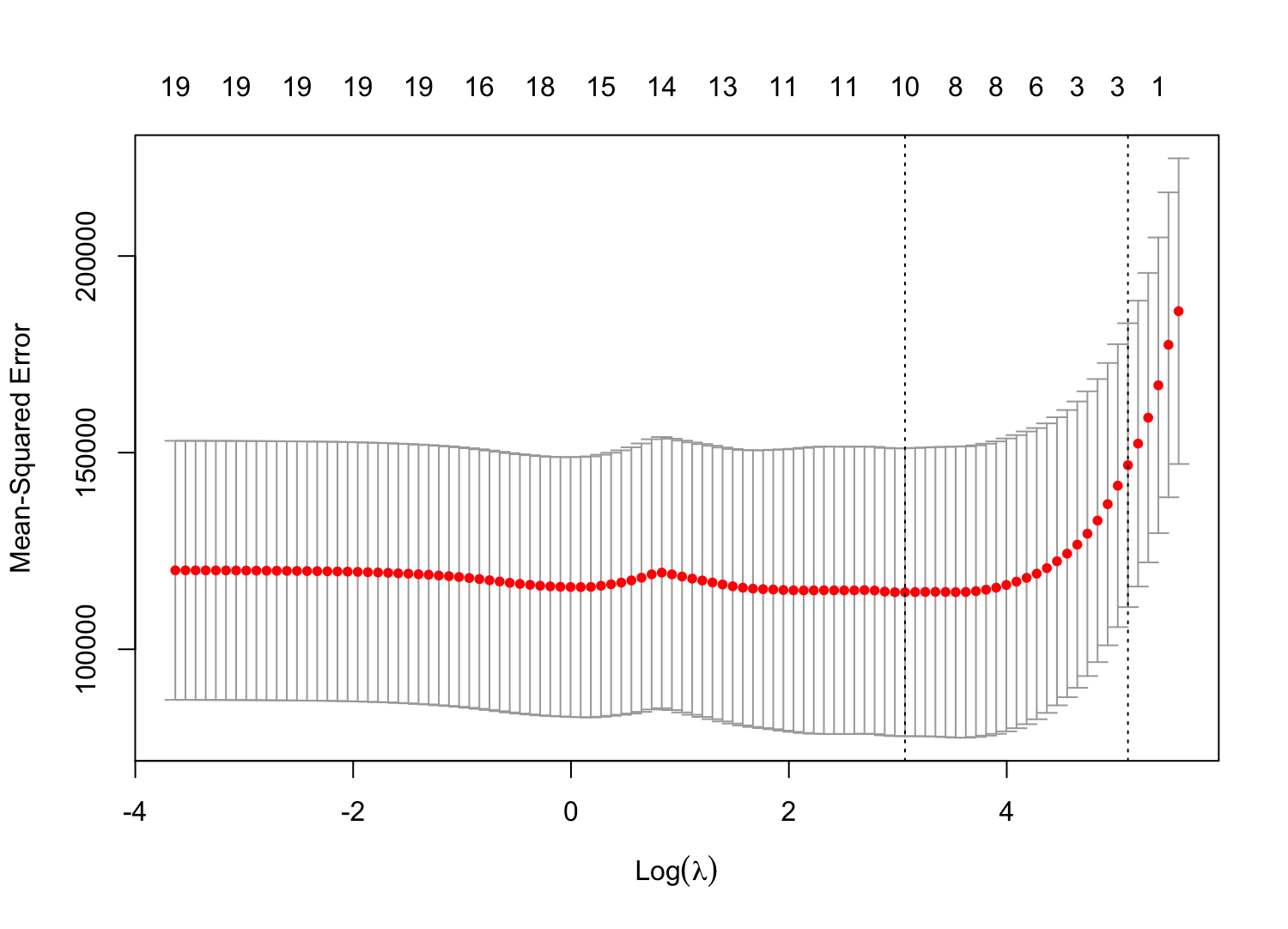

> bestlam = cv.out$lambda.min; bestlam
[1] 21.45407
> yhat = predict(lasso.mod, newx = x[test, ], s = bestlam)
> mean((y[test] - yhat)^2) # MSE of test data
[1] 141346.4

최적의 $\lambda$ 인 21.45407로 계산한 MSE는 141346.4로, LSE보다 좋은 성능을 보인다.
Ridge Regression에서의 Test MSE와 유사한 값이다.

> out = glmnet(x, y, alpha = 1, lambda = grid)
> lasso.coef = predict(out, type = "coefficient", s = bestlam)[1:20,]
> lasso.coef[lasso.coef!=0]
(Intercept)        Hits       Walks       CRuns        CRBI   DivisionW     PutOuts 
 30.1802892   1.8270990   2.1632633   0.2032989   0.4057870 -95.0481045   0.2088099

교차검증을 통해 선택된 변수는 단 6개로, Lasso는 변수선택 기능을 갖고있다는 것을 알 수 있다.

Another formula

Ridge Regression과 Lasso 계수 추정량을 아래와 같은 형식으로 나타낼 수도 있다.

\hat\beta^R=argmin_\beta\left[\sum_{i=1}^n (y_i-\beta_0-\sum_{j=1}^p\beta_jx_{ij})^2\right] s.t \ \sum_{j=1}^p \beta_j^2 \leq s

\hat\beta^L=argmin_\beta\left[\sum_{i=1}^n (y_i-\beta_0-\sum_{j=1}^p\beta_jx_{ij})^2\right] s.t \ \sum_{j=1}^p |\beta_j| \leq s

식을 자세히 보면, $\beta$ 에 대한 타원의 방정식이라는 것을 알 수 있다. 단 Ridge의 조건식은 $\beta$ 에 대한 원의 방정식, Lasso의 조건식은 마름모이다.

$p=2$ 일 경우,
Ridge : $\beta_1^2+\beta_2^2\leq s$ 로 정의된 원 내 모든 점 중 가장 작은 RSS를 갖는 점이 Coefficients가 된다.
Lasso : $|\beta_1|+|\beta_2|\leq s$ 로 정의된 마름모 내 모든 점 중 가장 작은 RSS를 갖는 점이 Coefficients가 된다.

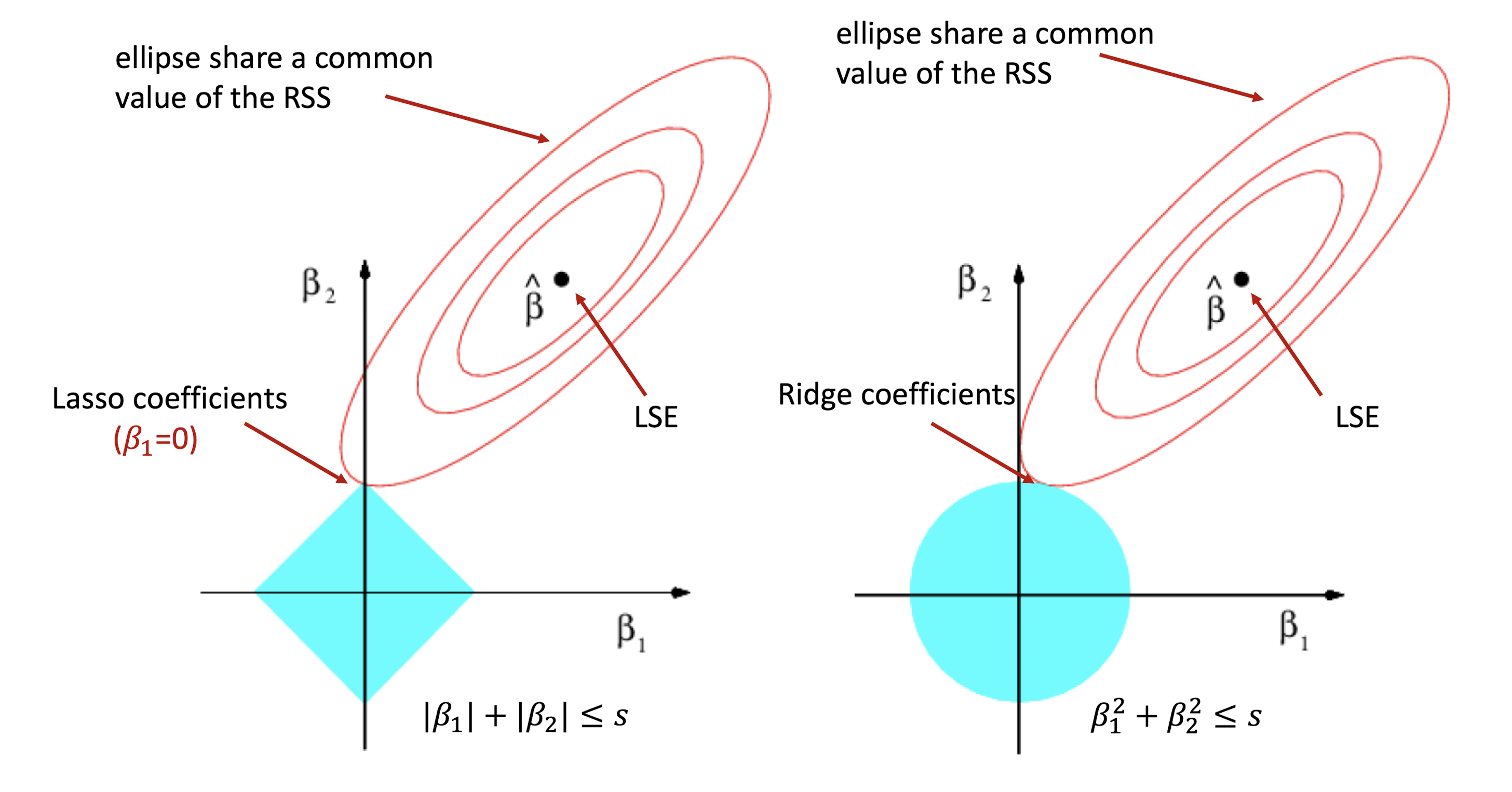
위 그림에서 타원의 선은 RSS가 동일한 지점을 시각화 한 것이다.

마름모의 경우에는 $\beta_1=0$ 인 지점에서 타원과 접할 수도 있지만, 원의 경우에는 그런 형태가 나오지 않는다는 점에서 Ridge Coefficient는 0이 될 수 없다는 점을 다시 상기할 수 있다.

Test MSE

$\lambda$ 가 증가하면 Ridge나 Lasso 모델의 flexibility가 감소한다. 따라서 Test MSE의 Bias는 증가하지만 Variance는 감소한다.

반면 $p>n$ 인 경우 Bias는 작고 Variance이 큰데, 이런 경우 Ridge나 Lasso가 잘 작동한다.

아래 그래프는 $n=50, \ p=45$ 에서 시뮬레이션한 결과를 나타낸 것이다.

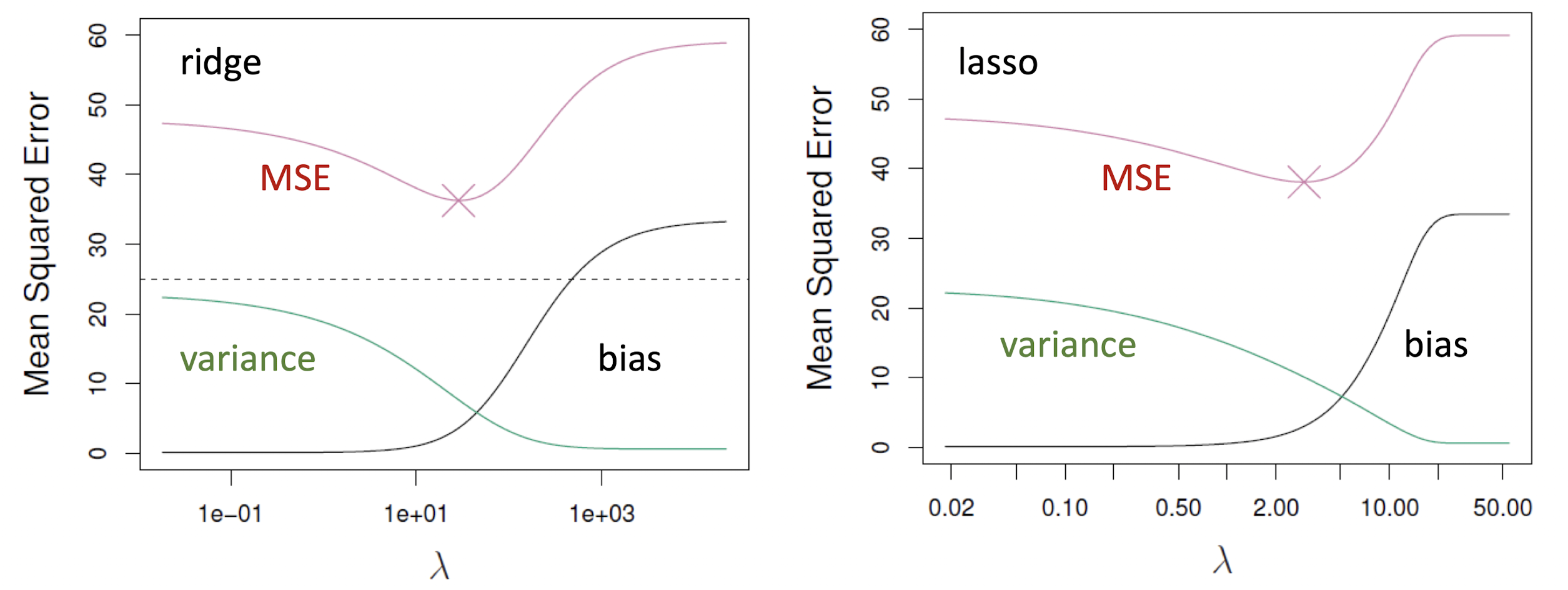
Comparing the Lasso and Ridge Regression

시뮬레이션에 따른 Ridge와 Lasso를 비교해보자. 점선이 Ridge, 실선이 Lasso의 값을 나타낸다.

Simulation 1 : $n=50, \ p=45$ 이며, 45개의 모든 설명변수가 반응변수와 연관된 경우
Simulation 2 : $n=50, \ p=45$ 이며, 두 개의 설명변수만이 반응변수와 연관된 경우

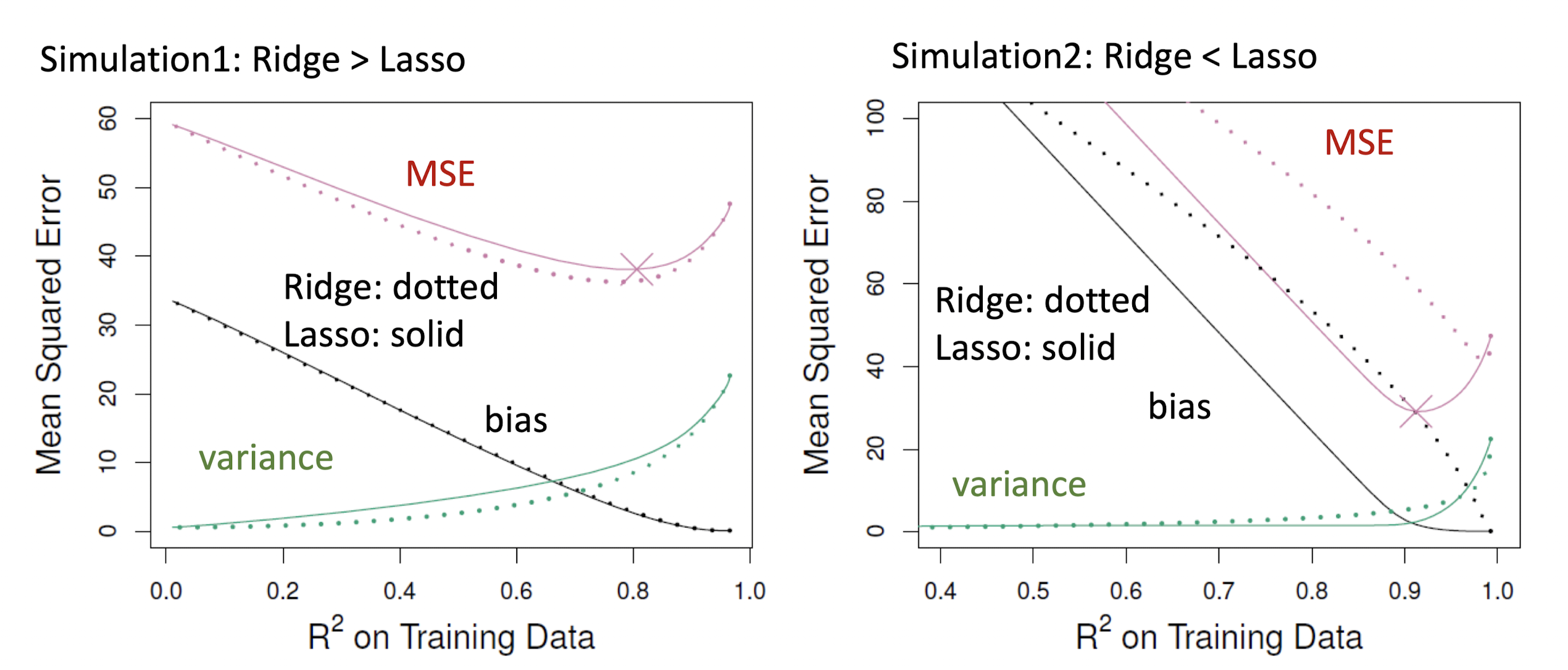
우선 $\lambda$ 가 증가함에 따라 분산은 커지고, 편향이 줄어든다는 점에서 두 방법은 비슷하다.

Lasso는 몇몇 $\beta_j$ 가 0이라는 가정을 하고 있으므로, Simulation 1에서 Ridge가 더 높은 성능을 보이는 것이 이상하지 않다. 반면 Simulation 2에서는 Lasso가 더 나은 성능을 보이고 있다.

Better Intuition about Ridge and Lasso

Ridge Regression과 Lasso를 좀더 직관적으로 파악하기 위해 간단하고 특수한 경우를 가정해보자.

y_i = \beta_i+\epsilon_i, \quad n=p

이 경우 LSE는 $\sum_{i=1}^p(y_i-\beta_i)^2$ 를 최소화하는 추정량이므로, $\hat\beta_i=y_i$ 가 된다. ( $i=1,...,p$ )

같은 상황에서 Ridge Regression은 $\sum_{i=1}^p(y_i-\beta_i)^2+\lambda\sum_{i=1}^p \beta_i^2$ 을 최소화하는 추정량을 갖는다.

식을 미분하여 최소가 되는 추정량을 구해보자. $\frac{\partial f(\beta)}{\partial \beta_i} = -2(y_i-\beta_i)+2\lambda \beta_i=0$ 을 만족하므로
Ridge Regression 추정량은

\hat\beta_i^R=\frac{y_i}{1+\lambda}

가 된다. 따라서 Ridge는 LSE를 일정비율( $1+\lambda$ )로 수축시킨다는 것을 알 수 있다.

비슷한 방법으로 Lasso 추정량은

\hat\beta_i^L= \begin{cases} \ y_i - \frac{\lambda}{2}, & y_i > \frac{\lambda}{2} \\ \ y_i + \frac{\lambda}{2}, & y_i < -\frac{\lambda}{2} \\ \ 0, & |y_i|\leq\frac{\lambda}{2} \end{cases}

가 된다. 즉, Lasso는 LSE를 일정한 양( $\frac{\lambda}{2}$ )만큼 수축시키며, 절댓값이 $\frac{\lambda}{2}$ 보다 작은 경우에는 0으로 만든다.

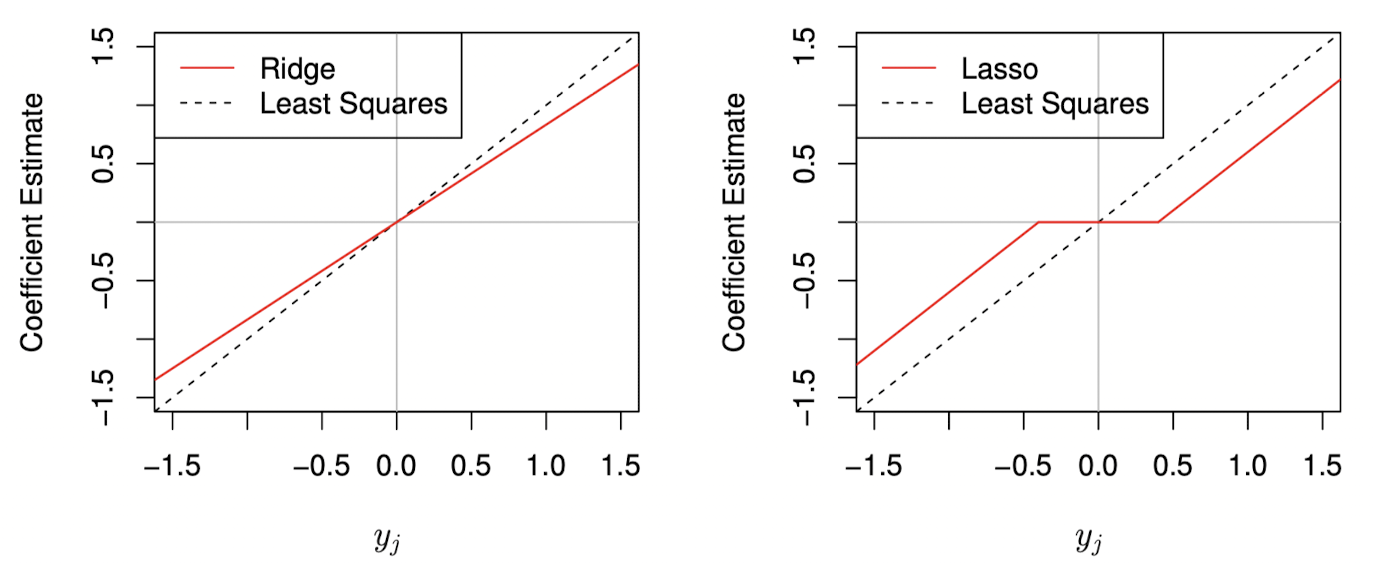
위 그림을 보면, Ridge의 경우 각 계수 추정치들이 동일한 비율로 수축된다. 반면 Lasso는 동일한 상수값만큼 수축시키며, 절댓값이 $\frac{\lambda}{2}$ 보다 작은 경우 0으로 만드는 것을 볼 수 있다.

sunnyboy

Data Analysis, ML, Backend 이것저것 합니다

이전 포스트

[R] Linear Model Selection

다음 포스트