🏆 학습목표
- 경사하강법과 역전파 알고리즘에 대해 이해하고 설명할 수 있다.
- 경사하강법과 역전파 알고리즘을 사용하여 신경망을 구현할 수 있다.
- 케라스 프레임워크를 이용하여 모델을 구축할 수 있다.
🌈Warm up
-
신경망의 학습과정, 경사하강법

① 입력 값을 Y= w * x + b 모델 식에 넣어 예측값을 구함
② 예측 값에서 정답을 뺀 것이 오차(계산을 쉽게 하려고 제곱)
③ 모든 학습 데이터의 오차를 모두 더하면 이차함수 그래프 나옴
④ 이때 접선의 기울기가 0이면 오차가 최소가 됨
⑤ 오차함수에서 w와 b로 각각 편미분을 하면 (w,b)=0인 두 개의 식 생성
⑥ 이걸 연립방정식으로 풀면 w와 b를 구할 수 있음
⑦ 미분이 0인 오차의 최솟값을 한 번에 구하는 방법 = 최소제곱법 -
문제점: 노드의 개수가 많아지면 연립방정식이 넘 복잡해짐
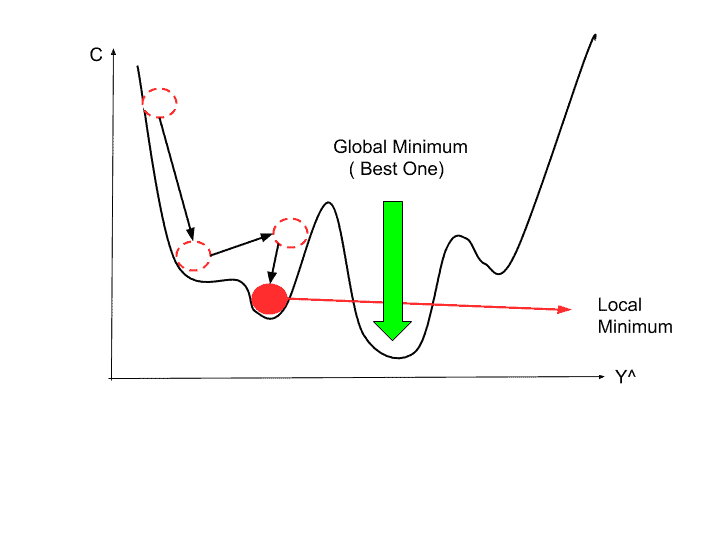
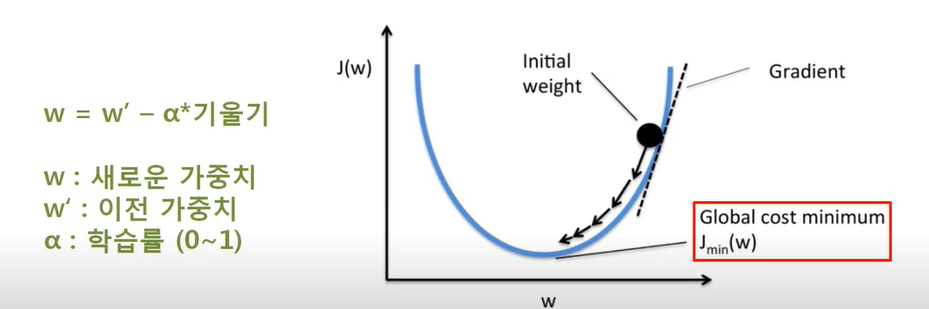
✨경사하강법: 오차의 최소값을 한 번에 안 찾고, 현재 가중치 w의 위치에서 오차가 작아지는 방향으로 조금씩 이동하면서 가중치를 수정합니다.
오차함수를 미분한 기울기만큼 가중치를 변경하는데 여기서 학습률인 알파로 이동속도를 조절합니다. 이 과정을 계속 반복하면 오차의 최소값에 근접하게 되고 그 때 가중치 파라미터가 신경망이 학습한 지능이다.
경사하강법의 문제점: 다층신경망의 경우 오차 함수에 모든 노드의 식이 연결되어 있다. 그래서 이를 미분하는데 엄청나게 시간이 걸린다. 1980년대 오차 역전파라는 방법을 발견해 가장 마지막 노드인 출력에서 한 번만 미분을 하고 그 결과를 뒤의 노드로 전달하면서 재사용합니다. 덕분에 빠른 속도로 학습이 가능해졌고 신경망이 다시 주목을 받았다.
🔥Class
역전파
- 역방향으로 가중치를 업데이트 하는 알고리즘.
ex) 시험 공부 오답 노트?, 스챌 이후의 회고
경사하강법