정수 삼각형(프로그래머스-동적계획법)

문제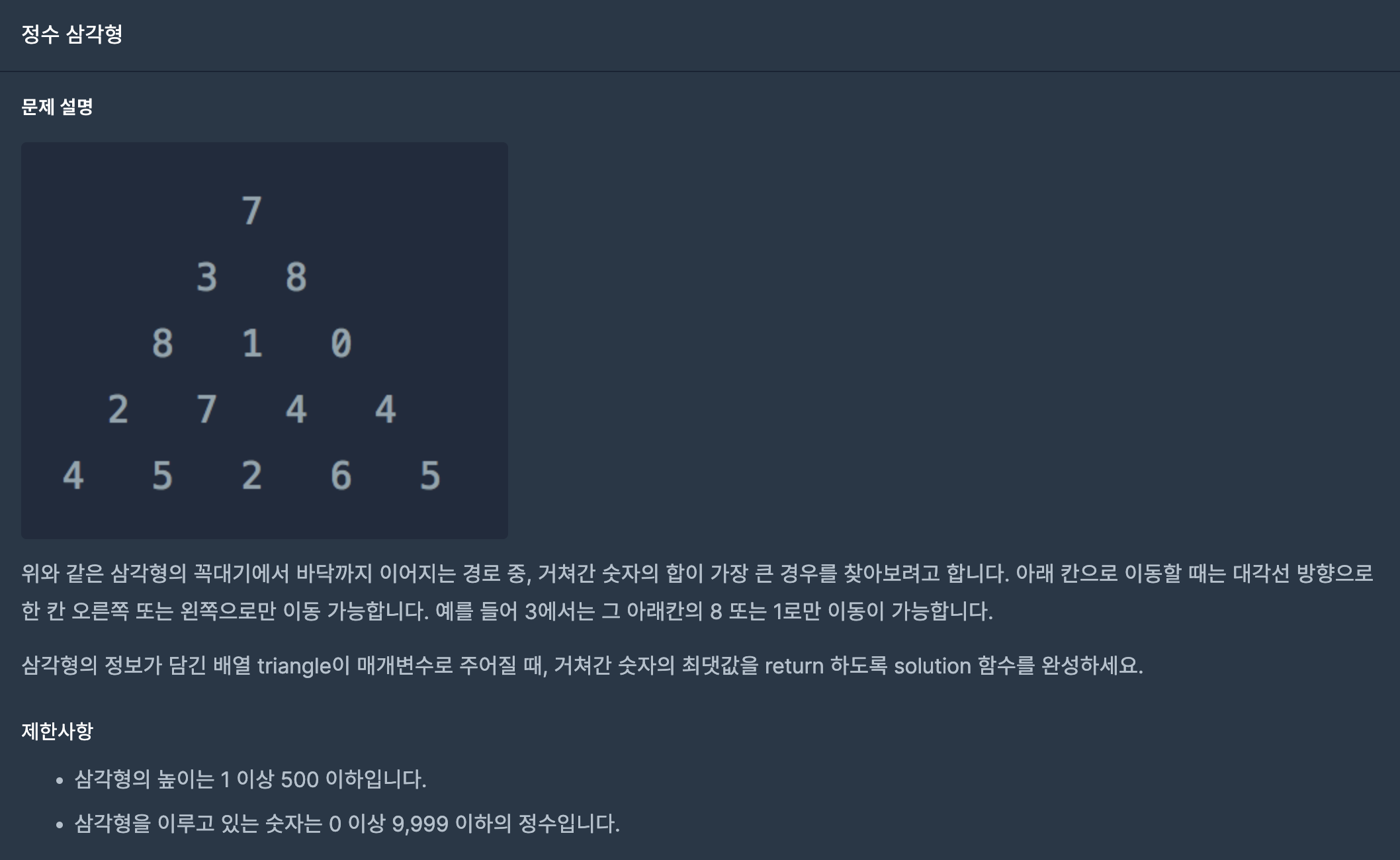

코드

class Solution {
    public int solution(int[][] triangle) {
        int answer = 0;
        int[][] dp=new int[triangle.length][];
        for(int i=0;i<triangle.length;i++)
            dp[i]=triangle[i].clone();
        dp[0][0]=triangle[0][0];

        for(int i=0;i<triangle.length;i++){
            for(int j=0;j<triangle[i].length;j++){
                if(i==triangle.length-1){
                    answer=Math.max(answer,dp[i][j]);
                    continue;
                }
                dp[i+1][j]=Math.max(dp[i+1][j],dp[i][j]+triangle[i+1][j]);
                dp[i+1][j+1]=Math.max(dp[i+1][j+1],dp[i][j]+triangle[i+1][j+1]);
            }
        }
        return answer;
    }
}

풀이

(1) triangle 배열과 같은 크기의 dp 배열을 만들어 준다. (dp 배열의 각 요소에는 누적 합의 최댓값이 들어갈 예정이다.)
(2) 반복문으로 dp의 한 행씩 돌면서, 다음 행의 누적 합의 최댓값을 갱신한다.
(3) 마지막 행까지 완료하면, 마지막 행의 요소들 중 최댓값을 answer로 반환한다.

결과

정말 기본적인 dp문제라고 생각한다.
하지만 나는 쉽게 풀지 못했다.
처음에는 dfs로 풀 수 있을 것이라 생각해고 풀었더니, 시간초과가 났다. 제한사항에서 최대 높이가 500이라는 것만 보고 크기가 작다고 생각한 것이다.
하지만 좀만 생각해보면, 한 요소에서 한칸씩 내려갈 떄마다 두가지 경우의 수로 나뉘는데 이게 500번 쌓이면 시간복잡도가 어마어마하게 높아진다는 것을 알 수 있었다.
그래서 원래 이 문제의 카테고리인 dp로 다시 풀었다.
나는 누적합 중 나올 수 있는 가장 큰 수인 5000000 크기의 dp 배열을 만들어 놓고, 0부터 5000000까지 돌면서 최대 값을 갱신하는 방식으로 했는데, 결과적으로는 틀린 방식이었다.

힌트를 살짝 봤는데, 보자마자 바로 깨달았다.
전형적인 dp 풀이로 풀면 된다는 걸 그제서야 꺠달았다.
왜 이렇게 쉬운 방법이 생각나지 않았을까.

그리고 이 문제를 풀면서 원래 아무생각 없던 것도 의문이 생겼다.
int[][] arr={{1,2},{3},{1,2,3}};
이런 게 원래 되는거였나?
다차원 배열은 원래 행,열 크기가 고정되어 있는것이 아니었나?
라는 생각이 들었다.
사실 다차원 배열이라는게, 배열의 배열이다.
위 배열의 예시로,
arr의 첫번째 행은, [1,2]라는 배열의 참조값을 가지고 있는 것이다. (참조값은 메모리 주소와 다른 개념이다. 다른 언어와 달리 자바에서는 jvm이 참조값이라는 것을 관리한다고 한다.)
결과적으로, 각 행은 배열을 가리키는 참조값을 가지는 것이기 때문에 그 가리키는 배열이 크기가 어떻든 상관이 없다.

이러한 기본적인 개념도 놓치지 않도록 하자.

출처 : 프로그래머스 코딩 테스트 연습 https://school.programmers.co.kr/learn/challenges