
선형 회귀
집의 크기로 집의 값을 예측하는 경우를 생각해봅시다.
선형 회귀는 데이터에 가장 적절한 하나의 선을 찾아냅니다. 이 선을 최적선이라 합니다.
이 선을 통해 새로운 집의 크기에 대한 집의 값을 예측할 수 있습니다.
선형 회귀 용어
선형회귀는 지도학습, 비지도학습, 강화학습 중 지도학습 알고리즘에 해당합니다.
그리고 지도학습 내 분류랑 회귀 중 회귀에 해당합니다.
선형 회귀에서 맞추려고 하는 값을 목표 변수라 합니다.(target variable/output variable)
그리고 맞추는데 사용하는 값을 입력 변수라 합니다.(input variable/feature)
학습 데이터의 개수를 보통 m으로 나타냅니다. 입력 변수는 x, 목표 변수는 y로 표현합니다. x와 y의 위에 괄호로 어떤 데이터에 해당하는 건지 적어줍니다.
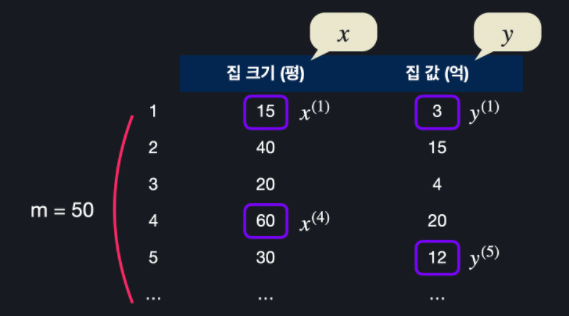
가설 함수
최적선을 찾기 위해 시도하는 함수 하나하나를 가설 함수라 합니다. 가설 함수가 hypothesis function이므로 h로 표현합니다. 또한, 계수는 일관성 있게 θ로 표현합니다.

평균 제곱 오차(MSE)
가설 함수를 평가하는 방법으로 평균 제곱 오차(Mean Squared Error)를 사용합니다. MSE는 데이터와 가설함수가 평균적으로 얼마나 떨어져 있는지 나타냅니다.
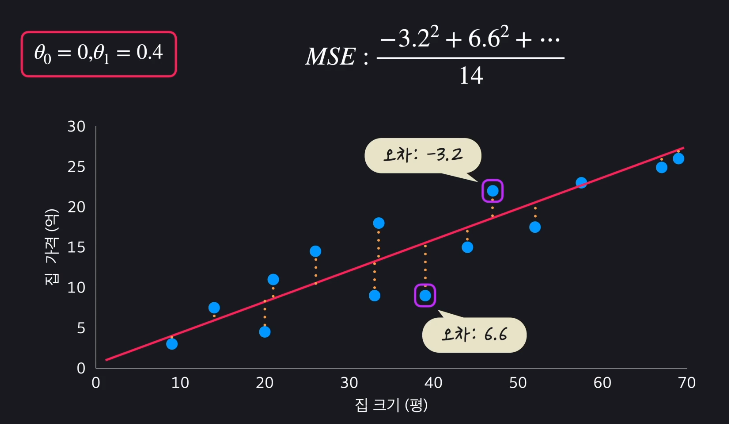
제곱을 더하는 이유는 모든 오차를 양수로 통일하고, 더 큰 오차를 부각시키기 위함입니다.
평균 제곱 오차 일반화
다음 식이 평균 제곱 오차의 일반화식입니다.
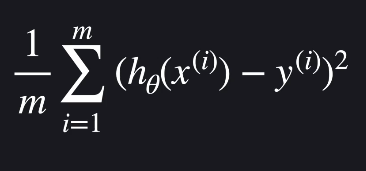
손실 함수(Loss Function)
손실 함수는 비용 함수(Cost Function)이라고도 합니다.
손실 함수는 가설함수의 성능을 평가하는 함수이고, 보통 J라는 문자를 씁니다.

선형회귀에서는 평균제곱오차(MSE)가 손실함수의 output입니다. 분모에 2를 곱한 것은 계산의 편리성 때문입니다.
변수가 x인 가설함수와 다르게, 손실 함수는 θ가 변수입니다.
θ값들을 바꿔 손실 함수의 아웃풋을 최소화시켜야 합니다.
θ를 아래와 같이 따로따로 적어도 되는데, 보통 θ하나로 묶어서 표현합니다.
경사 하강법 개념
손실함수의 극소점을 향해 가는 방법입니다. 기울기 벡터는 가장 가파르게 올라가는 방향을 알려주므로, -1을 곱해 가장 가파르게 내려가는 방향으로 이동합니다.
경사 하강법 테크닉
학습률 α는 경사를 타고 내려갈 때, 얼마나 많이 움직일지 그 정도를 나타냅니다.
이를 적용한 경사 하강법의 일반화는 다음과 같습니다. (θ를 업데이트 해나가기)
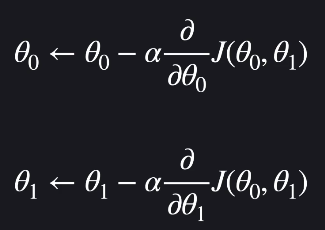
이를 계산한 결과는 다음과 같습니다.
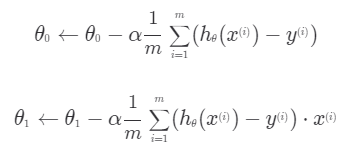
입력변수 x와 목표 변수 y를 하나의 값이 아니라 벡터로 생각할 수 있습니다.
또한, 경사하강법 식은 다음과 같이 표현도 가능합니다.
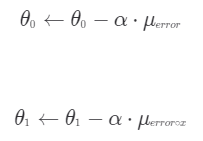
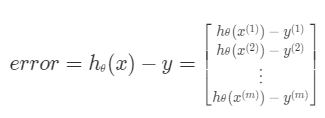
이때, 주의할 점은 순서대로 업데이트 할 때, 뒷 순서에도 바뀌기 전 값을 넣어줘야 한다는 것입니다.
경사 하강법 구현 시각화
import matplotlib.pyplot as plt
plt.scatter(house_size, house_price) #산점도
plt.plot(house_size, prediction(theta_0, theta_1, x), color='red') #가설함수
plt.show() #시각화학습률 알파
학습률 α가 크면, 경사 하강을 한 번 할 때마다 θ값이 너무 많이 바뀝니다.
심지어, α가 너무 크면 경사 하강법을 진행할수록 손실 함수 J의 최소점에서 멀어질 수도 있습니다.
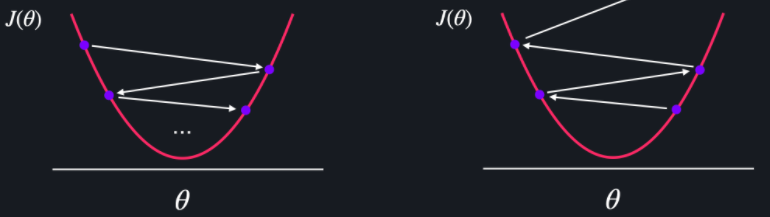
학습률 α가 작으면 찔끔찔끔 움직여서, 최소 지점을 찾는데 오래걸리게 됩니다. 즉 다음 그림처럼 iteration수가 너무 많아집니다.
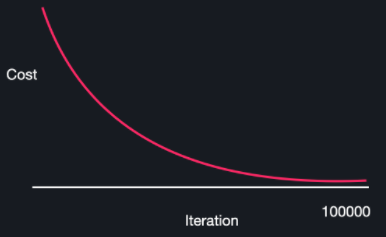
일반적으로 학습률은 1.0~0.0 사이로 여러 개를 실험해보면서, 경사 하강을 제일 적게 하면서 손실이 잘 줄어드는 학습률을 선택합니다.
모델 평가하기
가설함수는 모델이라고 부릅니다. 또한, 데이터를 이용해서 모델을 개선시키는 것을 모델을 학습시킨다고 합니다.
모델을 평가하는데는 평균 제곱근 오차를 사용하는데, 평균 제곱 오차에 단위를 맞추기 위해 루트를 씌운 값입니다.
하지만, 주어진 데이터에 맞게 학습시켰으므로, 평균 제곱 오차는 낮을 수 밖에 없습니다. 따라서 학습 데이터(training set)와 평가 데이터(test set)를 나눕니다.
scikit-learn 소개 및 데이터 준비
scikit-learn(sklearn) 라이브러리에 머신러닝 알고리즘이 들어있습니다. 또한, 교육용 데이터를 제공합니다.
from sklearn.datasets import load_boston #boston집값 데이터셋
import pandas as pd #pandas DataFrame 쓰기위해
boston_dataset = load_boston()
print(boston_dataset.DESCR) #데이터셋 정보 보기
boston_dataset.feature_names #속성이름들
boston_dataset.data #입력변수들이 행렬로
boston_dataset.data.shape #행렬 차원
boston_dataset.target #목표변수들이 행렬로
boston_dataset.target.shape #행렬 차원
x = pd.DataFrame(boston_dataset.data, columns = boston_dataset.feature_names)
x = x[['AGE']] #입력변수
y = pd.DataFrame(boston_dataset.target, columns=['MEDV']) #목표변수scikit-learn 데이터 셋 나누기
training set과 test set으로 데이터를 나눠야 합니다.
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x,y,test_size=0.2, random_state=5)
#20퍼를 테스트 셋으로 고릅니다.
#random_state에 정수를 적으면, 실행할때마다 항상 같은 데이터셋이 선택됩니다.scikit-learn으로 선형 회귀 쉽게 하기
from sklearn.linear_model import LinearRegression #선형회귀 모델 불러오기
from sklearn.metrics import mean_squared_error #평균제곱오차 구하기위해
model = LinearRegression()
model.fit(x_train, y_train) #모델 학습시키기
model.coef_ #θ1의 값
model.intercept_ #θ0의 값
y_test_prediction = model.predict(x_test) #test set에 대한 예측값
mean_squared_error(y_test, y_test_prediction) ** 0.5 #평균 제곱근 오차범죄율로 집 값 예측하기
# 필요한 라이브러리 import
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import pandas as pd
# 보스턴 집 데이터 갖고 오기
boston_house_dataset = datasets.load_boston()
# 입력 변수를 사용하기 편하게 pandas dataframe으로 변환
X = pd.DataFrame(boston_house_dataset.data, columns=boston_house_dataset.feature_names)
# 목표 변수를 사용하기 편하게 pandas dataframe으로 변환
y = pd.DataFrame(boston_house_dataset.target, columns=['MEDV'])
X = X[['CRIM']] # 범죄율 열만 사용
# train_test_split를 사용해서 주어진 데이터를 학습, 테스트 데이터로 나눈다
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state=5)
linear_regression_model = LinearRegression() # 선형 회귀 모델을 가지고 오고
linear_regression_model.fit(X_train, y_train) # 학습 데이터를 이용해서 모델을 학습 시킨다
y_test_predict = linear_regression_model.predict(X_test) # 학습시킨 모델로 예측
# 평균 제곱 오차의 루트를 통해서 테스트 데이터에서의 모델 성능 판단
mse = mean_squared_error(y_test, y_test_predict)
mse ** 0.5