
일차식과 일차 함수
선형대수학은 일차식(가장 높은 차수가 1인 다항식)이나 일차 함수를 공부하는 학문입니다.
일차 함수 표기법
f(x0,x1,...xn) = a0x0 + a1x1 + ... + anxn + b
행렬과 벡터
행렬은 수를 직사각형 형태로 나열한 것입니다. 행과 열을 셀때는 0이 아닌 1부터 셉니다.
벡터는 행 또는 열이 하나밖에 없는 행렬입니다. 그냥 벡터라고 하면, 열벡터를 보통 의미합니다. 벡터의 차원은 원소의 개수입니다.
벡터의 원소를 나타낼 때는 숫자 하나만 사용합니다.
행렬(A)은 대문자, 벡터(a)는 소문자로 표현합니다.
numpy로 행렬 사용하기
import numpy as np
A = np.array([
[1,-1,2],
[3,2,2],
[4,1,2],
[7,5,6]
]) #행렬 만들기
B = np.random.rand(3,5) #원소값이 0~1사이의 랜덤값인 3X5 행렬
C = np.zeros((2,4)) # 모든 원소가 0인 2X4 행렬
A[0][2] #1행 3열 가져오기(★index 0부터)행렬 연산 I(덧셈, 스칼라곱)
행렬을 더하기 위해서는 두 행렬의 차원(행의 수 X 열의 수)이 같아야 합니다.
행렬과 수(스칼라)를 곱하는 것을 스칼라곱이라 합니다.
행렬 연산 II(두 행렬의 곱)
행렬을 곱하는 방식은 내적곱과 외적곱이 있고, 우리는 내적곱을 먼저 봅니다.
mXn행렬과 nXp행렬을 곱하면, mXp행렬이 나옵니다.
앞행렬의 열의 수와 뒷행렬의 행의 수가 같아야 곱셈이 가능합니다.
행렬곱셈의 순서는 중요합니다. 순서를 바꾸면 계산이 불가능할 수 있습니다.
요소별 곱하기
행렬 곱셈 연산 중 요소별 곱하기는 같은 행,열에 해당되는 요소끼리 곱해서 새로운 행렬을 만드는 연산입니다. A∘B와 같이 표현합니다.
A * B # 두 행렬 요소별 곱하기numpy로 행렬 연산하기
import numpy as np
A = np.array([
[1,-1,2],
[3,2,2],
[4,1,2]
])
B = np.random.rand(3,3)
A + B #행렬덧셈
5 * A #스칼라곱
A @ B #행렬곱, np.dot(A, B)로도 작성가능
A @ B + (A + 2 * B) #섞어서 사용가능전치 행렬, 단위 행렬, 역행렬
전치 행렬(transposed matrix)는 행과 열을 바꾼 행렬입니다. 행렬 계산을 할 때 모양을 맞추기 위해 사용됩니다.

단위 행렬(identity matrix)에 어떤 행렬을 곱해도 기존 행렬이 그대로 나옵니다.

역 행렬(inverse matrix)는 곱해서 단위행렬이 나오는 행렬입니다.
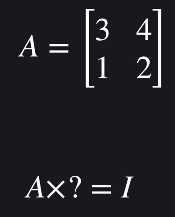
역행렬은 항상 정사각행렬이고, 모든 행렬에 역행렬이 있는건 아닙니다.
numpy로 전치, 단위, 역행렬 사용하기
import numpy as np
A = np.array([
[1,-1,2],
[3,2,2],
[4,1,2]
])
A_transpose = A.T #A의 전치행렬, np.transpose(A)로도 작성가능
I = np.identity(3) #3X3 단위행렬
A_inverse = np.linalg.pinv(A) #A의 역행렬, 역행렬이 없으면 비슷한 행렬 반환
A @ A_inverse #소수점 사용에서의 오차는 생김선형대수학과 행렬/벡터
일차식이 여러개 있는 선형 시스템을 행렬과 벡터를 통해 나타낼 수 있습니다.
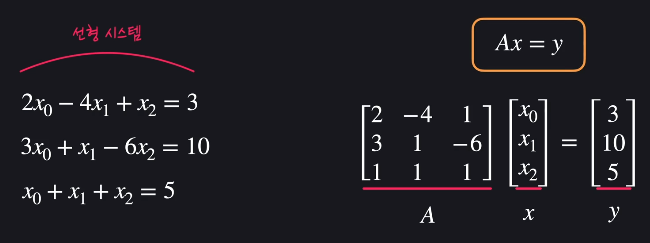
아무리 복잡한 선형 시스템도 행렬과 벡터로 쉽게 표현할 수 있습니다.
선형대수학이 머신 러닝에 필요한 이유
머신 러닝을 할 때는 데이터를 일차식에 사용하는 경우가 많습니다.
-> 행렬을 이용하면 정돈된 형태로 효율적이게 계산을 할 수 있습니다.
-> 선형 대수학은 일차식, 일차 함수, 행렬, 벡터를 다루는 학문이기 때문에 필수입니다.
