
함수
함수는 하나의 input에 대해서 하나의 output만 가집니다. input 변수가 2개 이상이면 다변수 함수라 합니다.
그래프
그래프는 수학식을 시각적으로 표현하는 방법입니다.
평균 변화율
f(b)-f(a) / b-a 또는 f(a+h)-f(a) / h 가 평균 변화율입니다.
순간 변화율
f(a+h)-f(a) / h 에서 h->0 일때의 값이 순간 변화율입니다.
미분
f(x+h)-f(x) / h 에서 h->0일때의 값은 f'(x)입니다.
가장 가파른 방향(2차원)
기울기가 음수면, x가 커질수록 y가 작아진다는 것입니다. 기울기는 어떤 방향으로 가야 가장 가파르게 올라갈 수 있는지 알려줍니다.
극소점, 극대점
극소점 중 가장 작은 점이 최소점이고, 극대점 중 가장 큰 점이 최대점입니다. 기울기가 평평해졌다가 다시 가팔라지는 안장점도 있습니다.
고차원에서 미분
다변수함수를 미분할때는 편미분을 합니다. 함수를 변수 하나에 대해서만 미분하는 것입니다. 편미분을 할 때 나머지 변수는 상수로 취급합니다.
가장 가파른 방향(고차원)
편미분으로 구한 기울기벡터는 그래프를 가장 가파르게 올라갈 수 있는 방향을 알려줍니다.
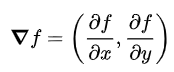
머신 러닝에 미분이 필요한 이유
함수를 미분하면, 특정 지점에서의 순간 변화율(기울기)을 알 수 있습니다. 머신러닝에서 함수의 극소점이 성능이 제일 좋을 때일 때, 그점을 찾기 위해서 미분이 필요합니다.
미분 챕터 퀴즈
경사는 항상 함수가 늘어나는 방향을 가르킵니다.
