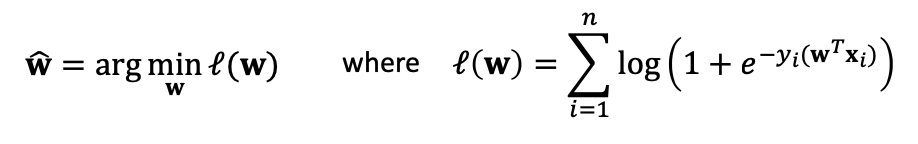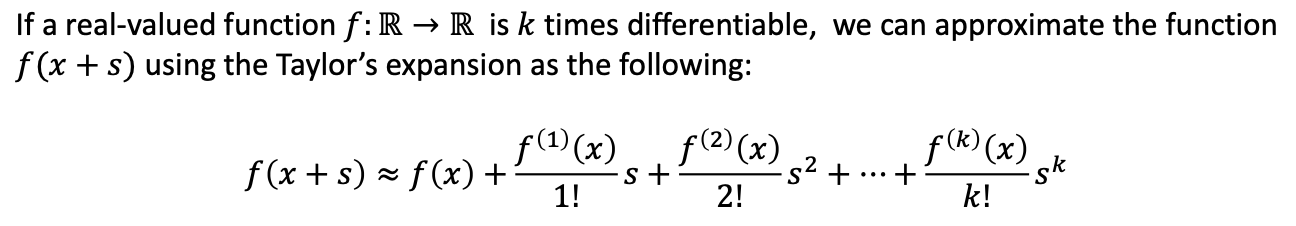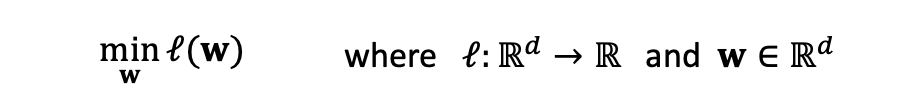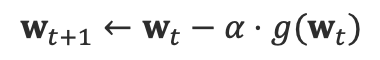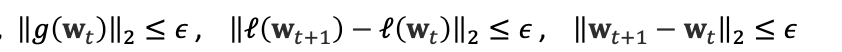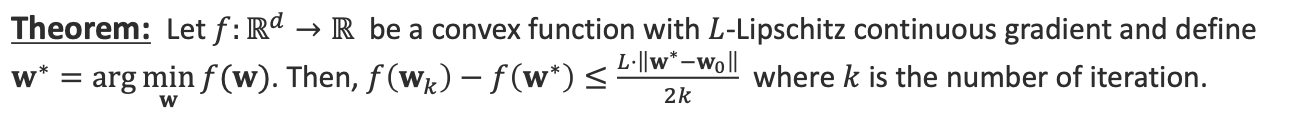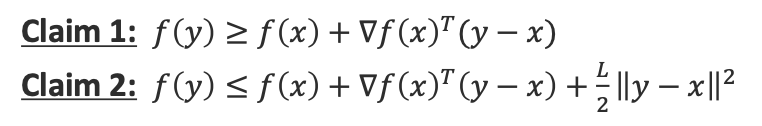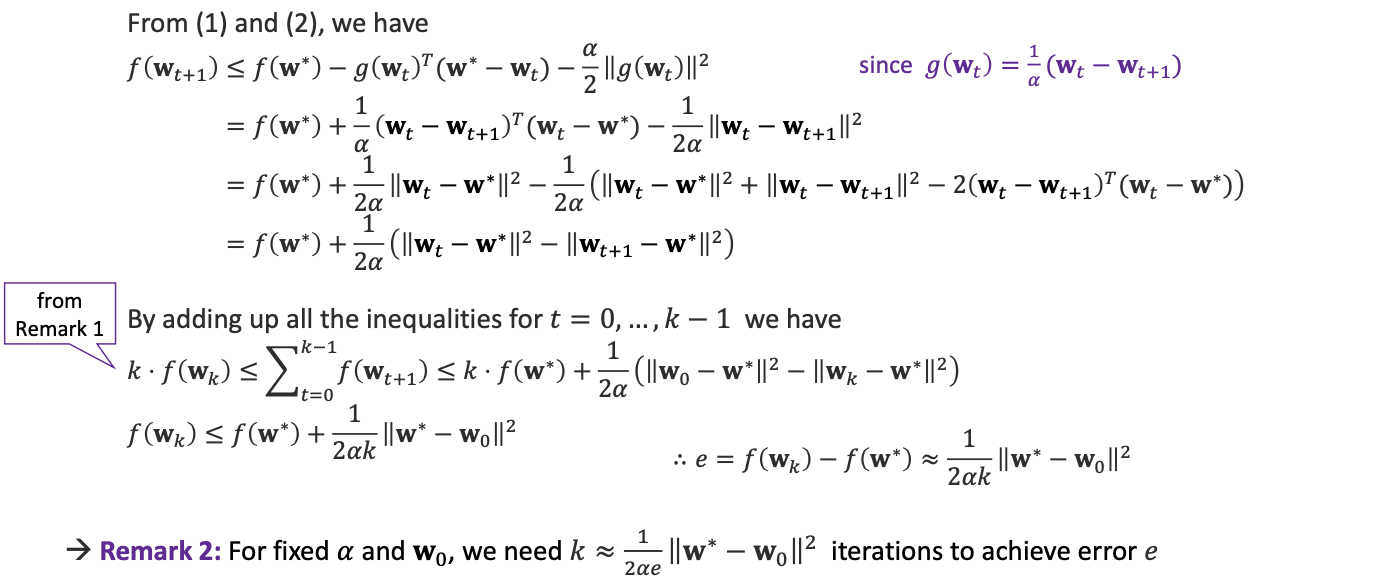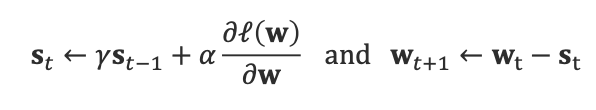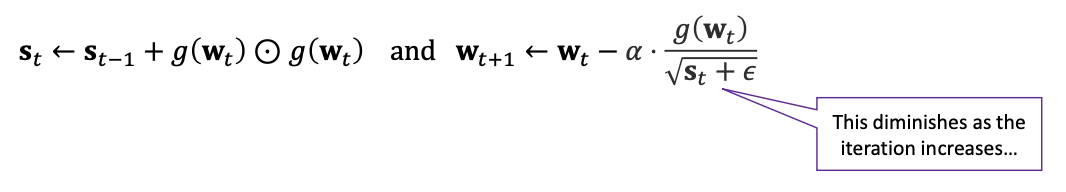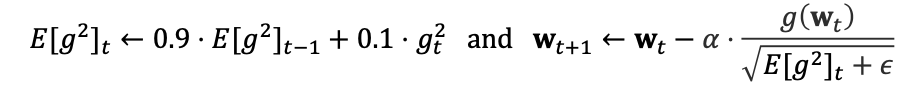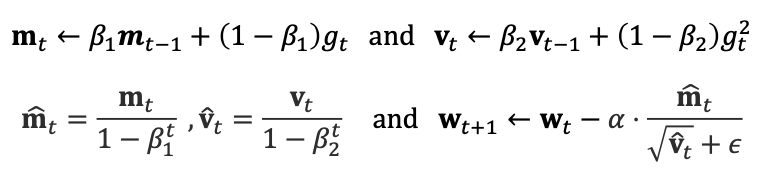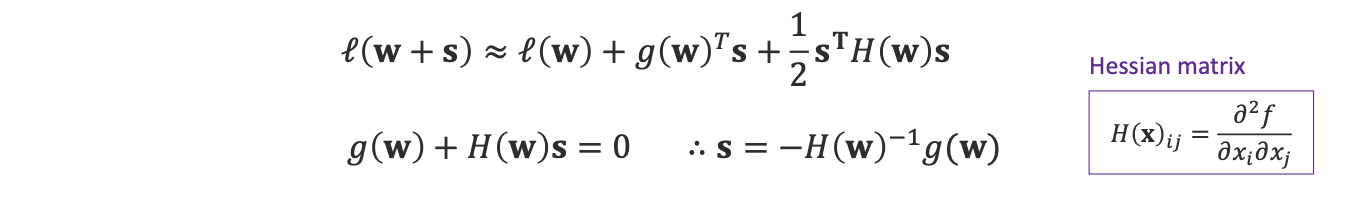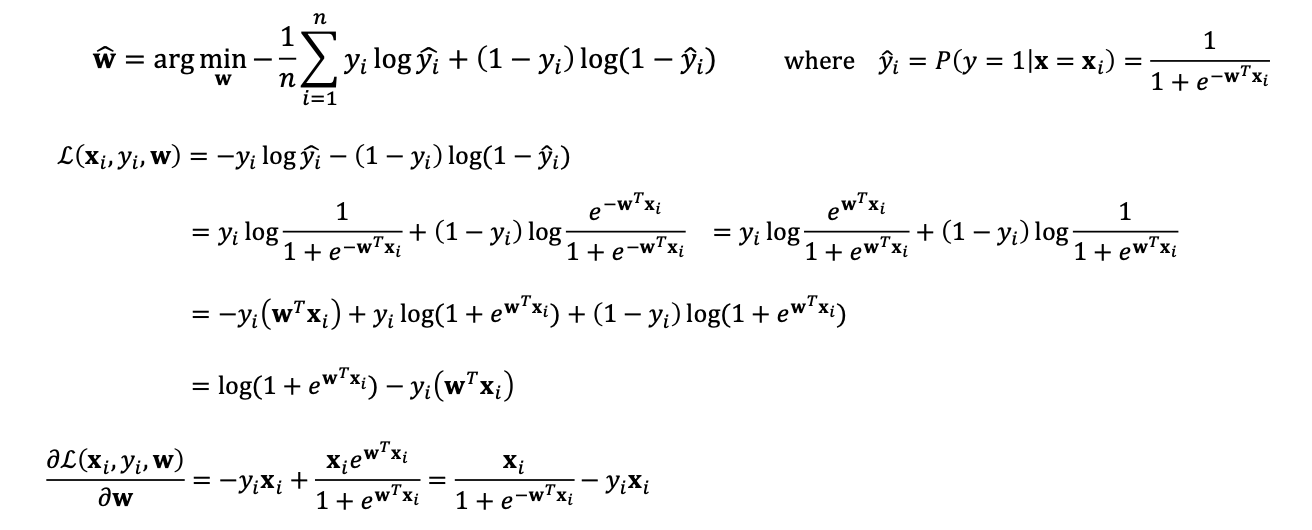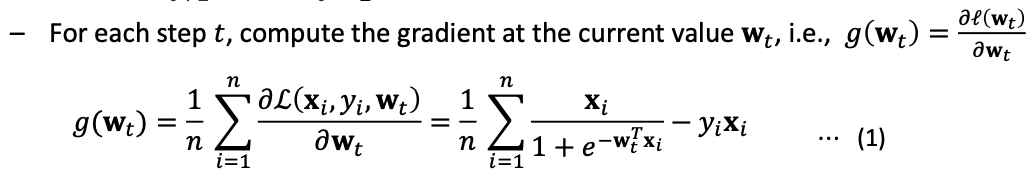Gradient Descent

지능 시스템을 위한 기계학습

"기계학습"
"ML"
강의: CORNELL CS4780 "Machine Learning for Intelligent Systems"

해당 포스트는 코넬대학교 CS4780과 그 강의 자료를 정리한 내용입니다.

---

이 글을 쓰게 된 계기

기계학습에 대한 전반적인 이해와 그 알고리즘을 학습해봅시다!

---

So, what is Gradient Descent?

천천히 알아가봅시다!

Optimizer?

Loss를 최소화 하거나 reward를 최대화 하는 알고리즘입니다! GD는 이의 일종입니다.

예시, Logistic Regression

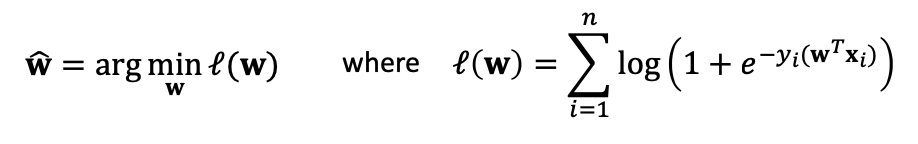
w와 bias를 최적화 하기 위해 GD를 사용할 수 있습니다.

then, what is Gradient?

러프하게 보자면 기울기 입니다.

Gradient descent

Gradient의 반대방향으로 파라미터를 조정하면서(ex: gradient가 음수이면 감소(-)하는 방향이므로 그의 반대로 파라미터를 증가) local minimum loss로 향하는 알고리즘.

사용하는 곳 :

closed form expresstion 이 있고, 최적해를 구하는게 불가능하거나, 어려울 경우에 사용합니다.

따라서 연속, 미분이 가능해야 합니다.

그리고 미분에 대하여 생각해봅시다..

Taylor's Expantsion

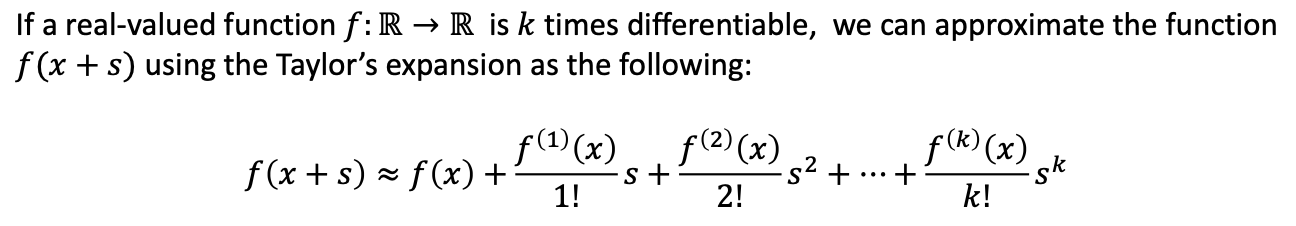
우린 이 테일러 급수를 이용하여 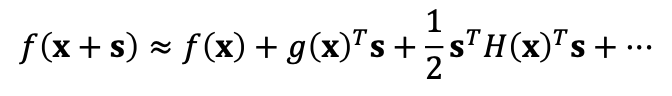과 같은 식을 세울 수 있습니다.

헤시앙을 이용하여 이차미분까지 표현하였으며 우리는 일차미분의 부분에 gradient를 사용합니다.

이때 우리는 최대 2차 근사 까지만 사용합니다.

3차부터는 매우 더럽고 치사합니다...

심지어 뒤의 수식은 1차까지만 사용합니다, 2차를 사용하지 않는 이유는 뉴턴 방법에서 보여드리겠습니다.

---

문제 정의, 수식 전개

Optimization Problem:

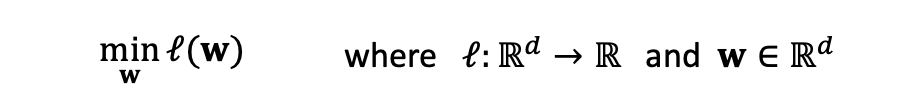
수식 전개

---

1. 초기값 w0 선정

---

2. w 업데이트

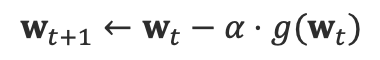
이때 $\alpha$는 step size로 우리가 설정해줘야 합니다

---

3. 수렴할 때 까지 2번 반복

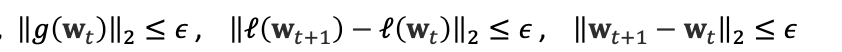
수렴 조건은 위와 같이 설정 가능

시각화

---

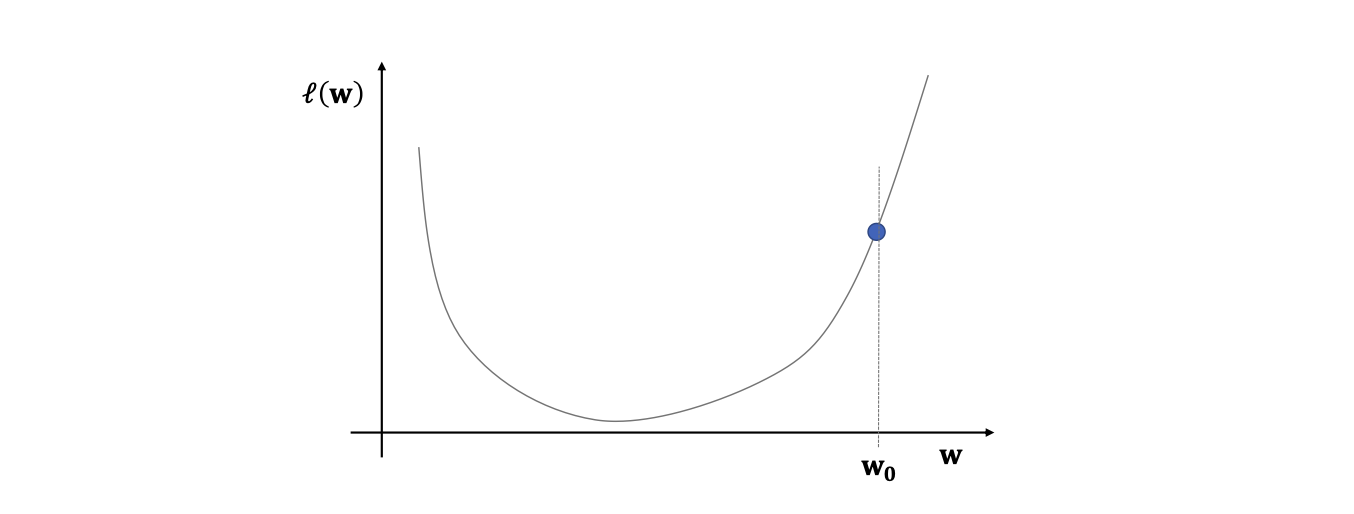
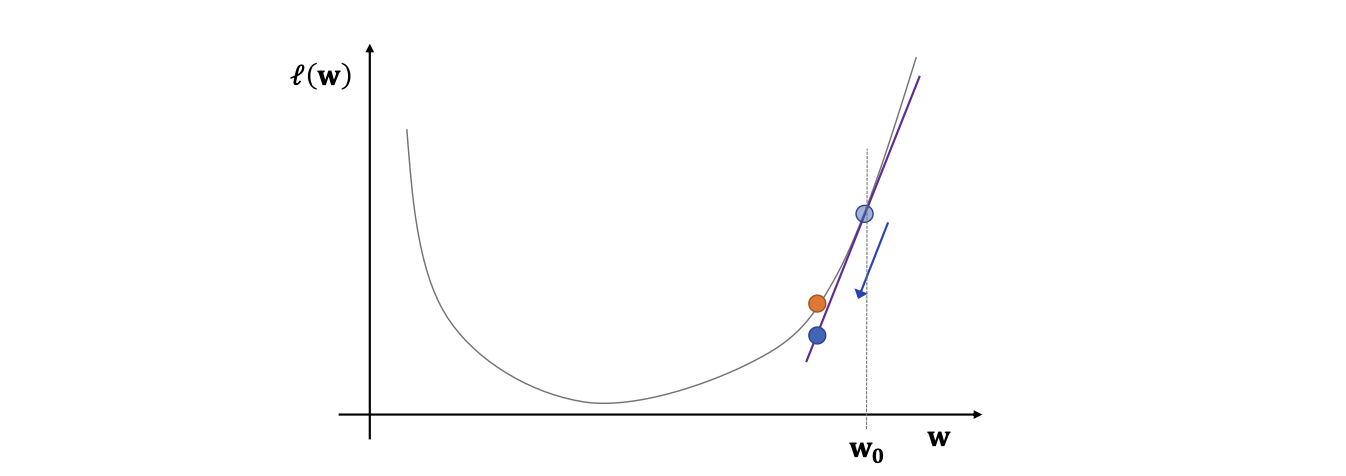
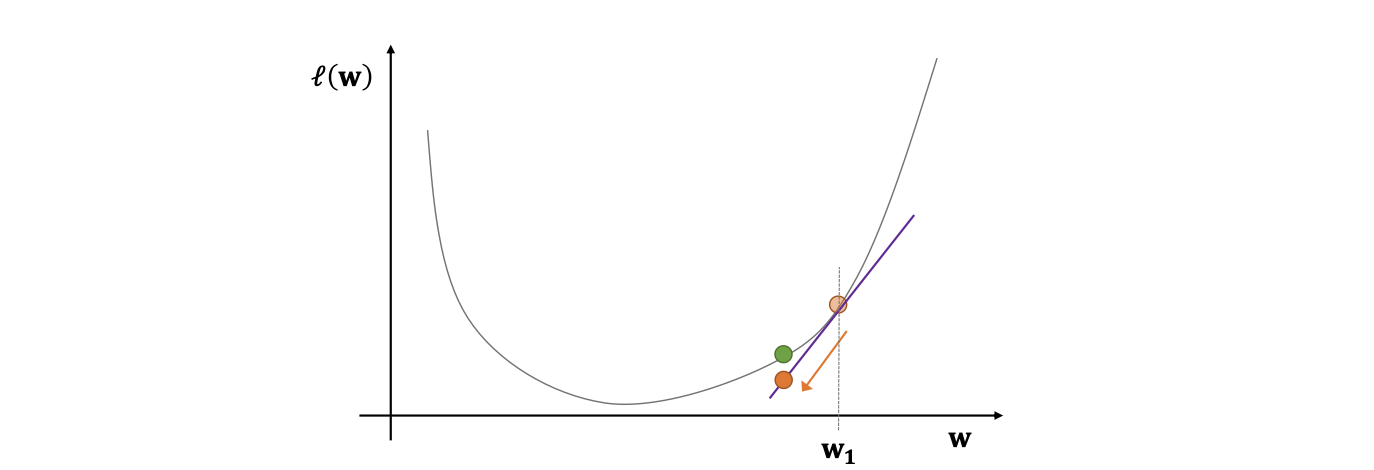
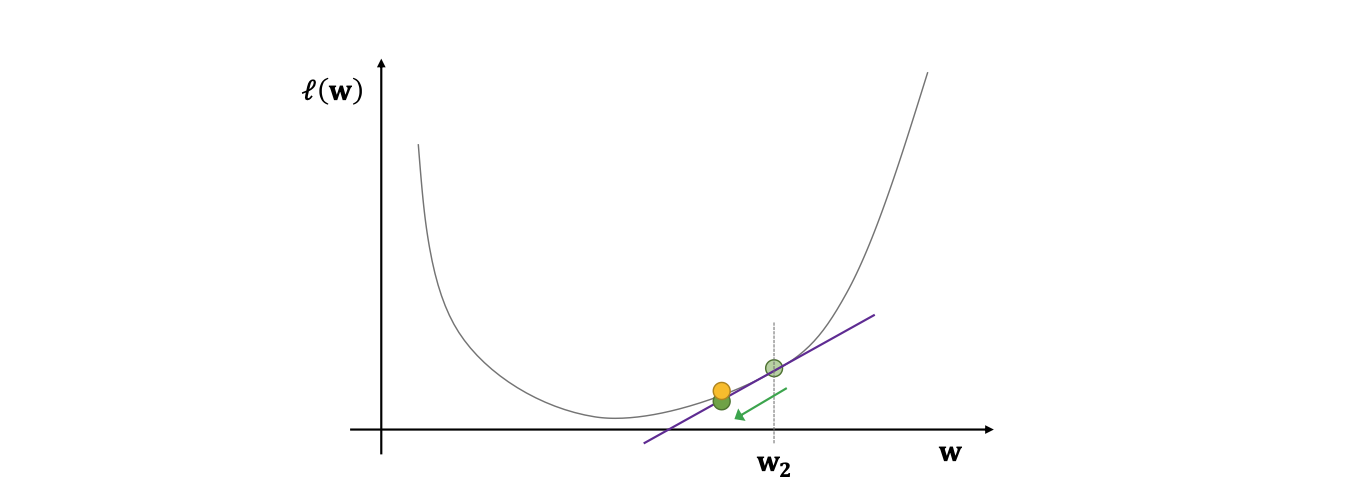
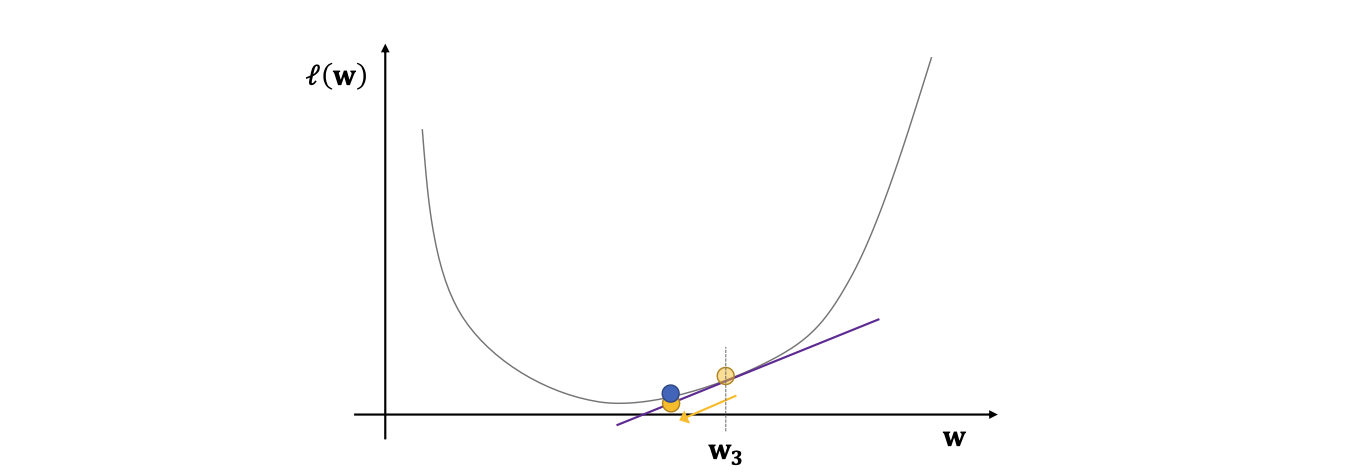
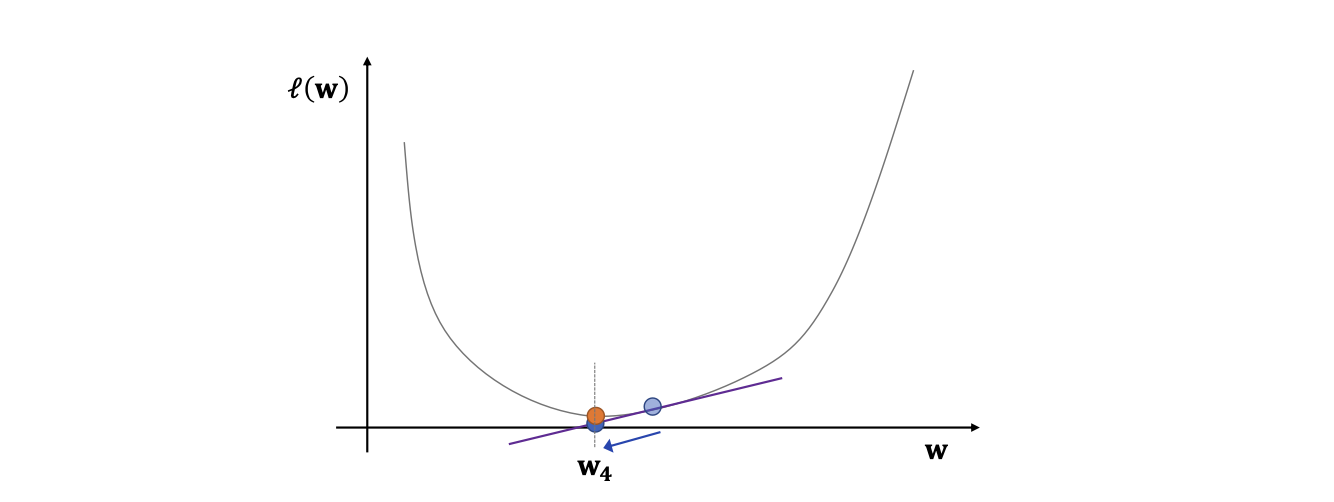
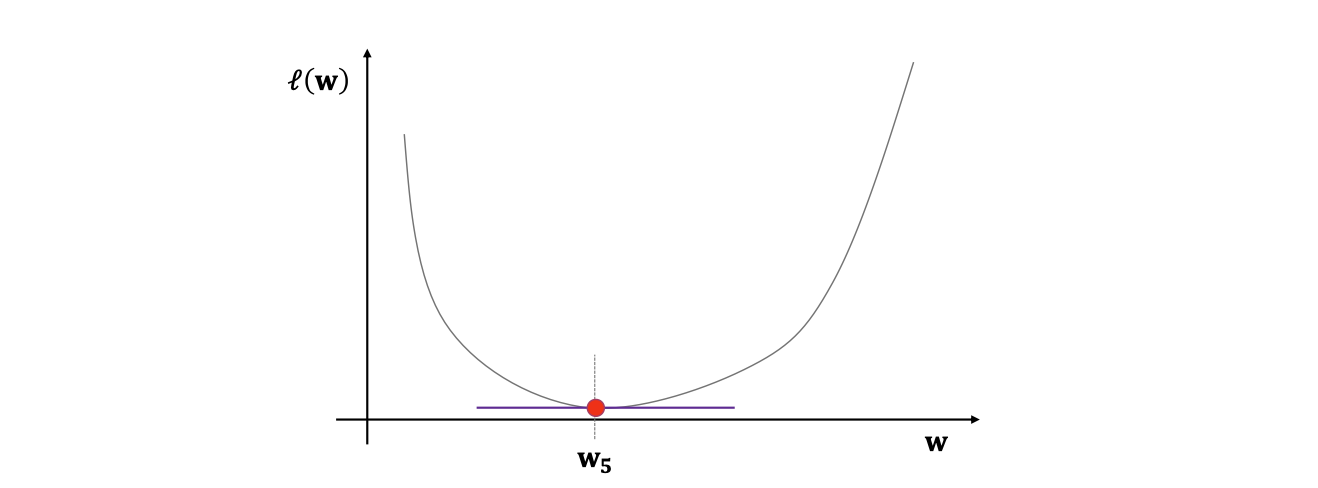
Gradient descent의 수렴성 정리

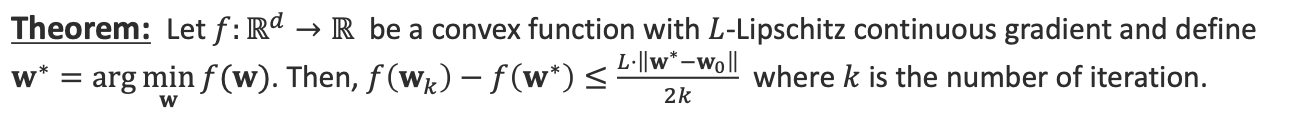
해석:

f를 L-Lipschitz 연속성 기울기를 가지는 convex한 함수라고 두고 w*를 정의합니다.

그렇다면 L-Lipschitz 연속성 정의에 의하여 위 수식이 성립합니다.

what is Convex? 라고 한다면...

이 두가지 조건을 만족시킨다면 convex하다고 할 수 있습니다.

이는 곧 최소값의 유일성과 같아집니다.

두가지 claim 과 함께 수식을 들고가보자구요

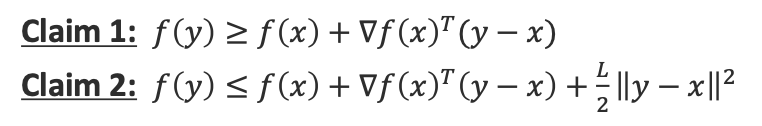
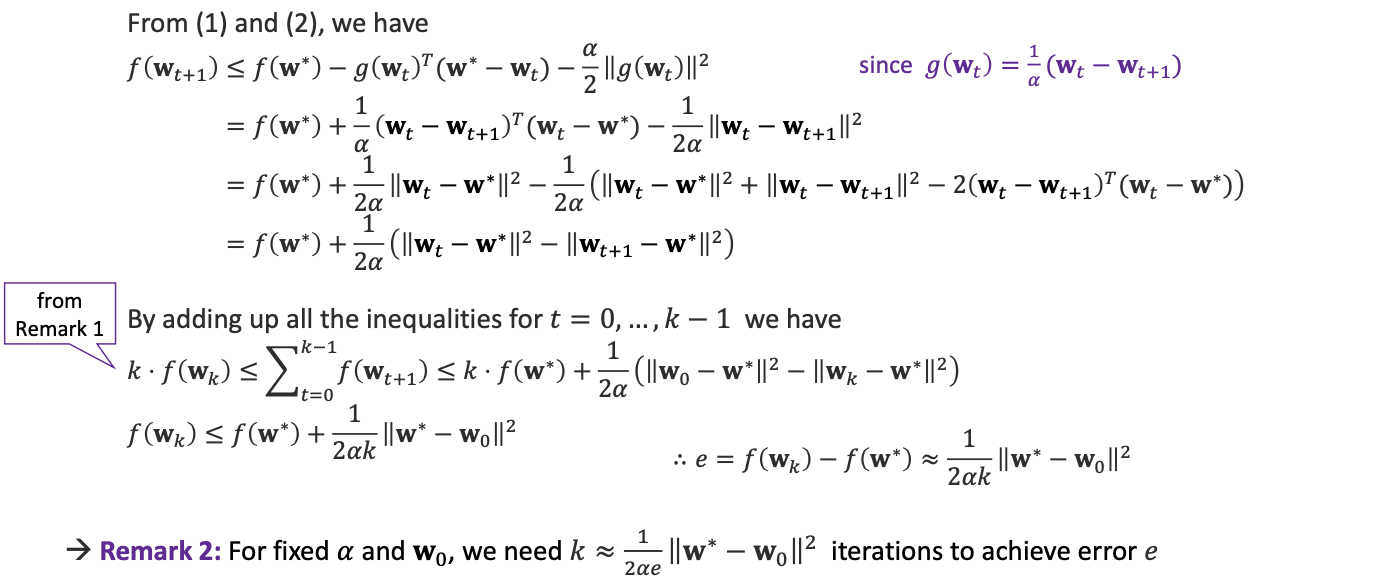
이런 과정을 통하여 우리는 Threorem을 증명했습니다!

참고사항

step size의 선정은 매우 중요합니다.

너무 크다면 발산할 것이고, 너무 작다면 미친듯이 오래걸릴 것 입니다.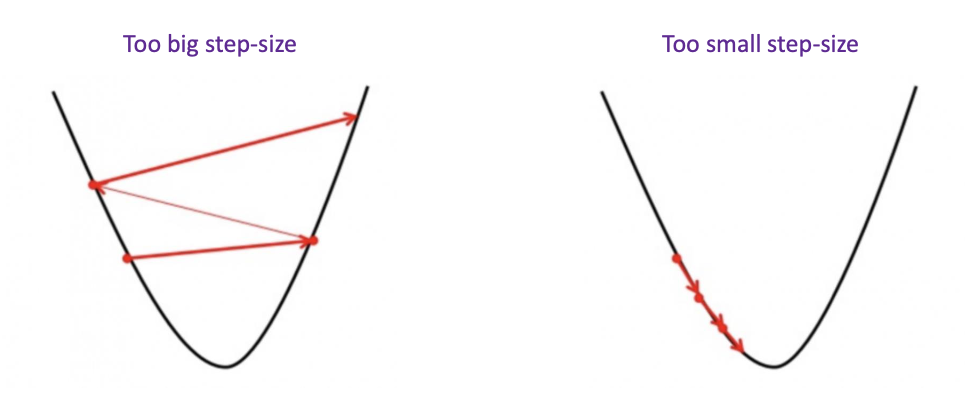

---

step size에 대한 문제를 해결할 방법?

고정된 step size가 아닌 다른 방법을 사용해보자.

• GD with Momentum

• AdaGrad (Adaptive Gradient Descent)

• RMS-Prop (Root Mean Square Propagation)

• Adam (Adaptive Moment Estimation)

1. GD with Momentum

직전 단계의 update를 고려한다.

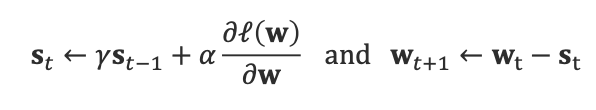
2. AdaGrad (Adaptive Gradient Descent)

빈번하게 사용된 애는 빠르게 넘긴다는 마인드

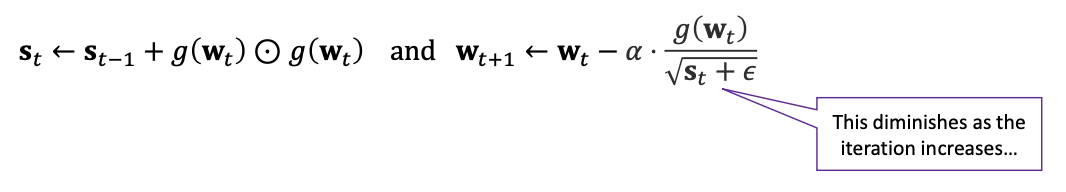
'⊙'에 대해 설명하자면 행렬의 원소곱이다.

3. RMS-Prop (Root Mean Square Propagation)

합 대신 평균을 이용하여 update, 너무 급격한 학습률 감소를 막는다.

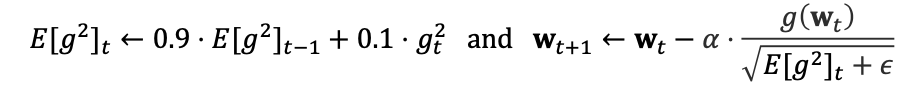
4. Adam (Adaptive Moment Estimation)

RMSprop의 특징인 평균과, 과거 gradient를 이용하는 Momentum을 섞었다.

---

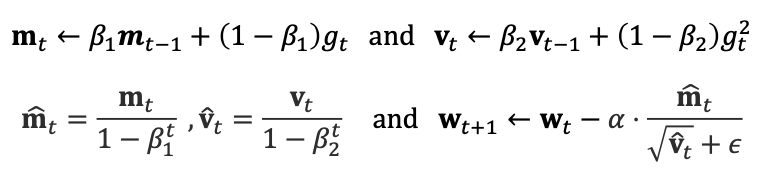
Disadvantages of Gradient Descent

한번에 모든 feature에 대하여 계산을 해야하기 때문에 시간이 너무 오래걸린다.

solution : (Mini-batch) Stochastic Gradient Descent

샘플의 미니 배치 or 그냥 배치를 사용하고, 학습 가능한 파라미터들을 자주 업데이트 하는 방식

---

참고

Newton’s Method:

이차미분식(헤시앙)까지 사용하여 계산, loss함수에 대하여 더 나은 근사가 가능하다, 최적해 까지도 빠르게 도달할 수 있다(이론상)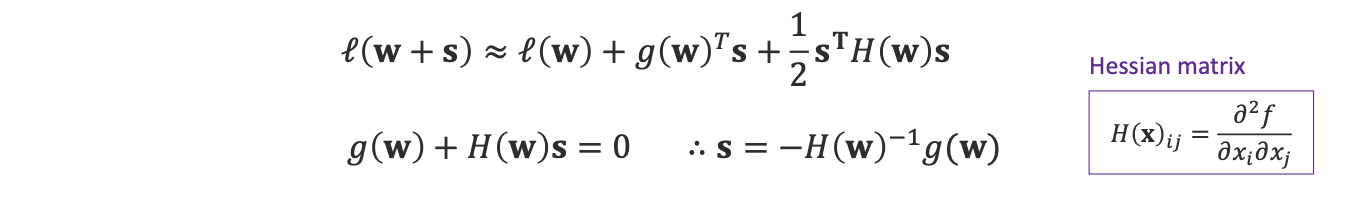

그러나 헤시앙 계산까지 고려하면 시간이 너무 오래 걸린다, stocastic과 반대의 상황.

이제 찐막, Logistic Regression에 적용해보자!

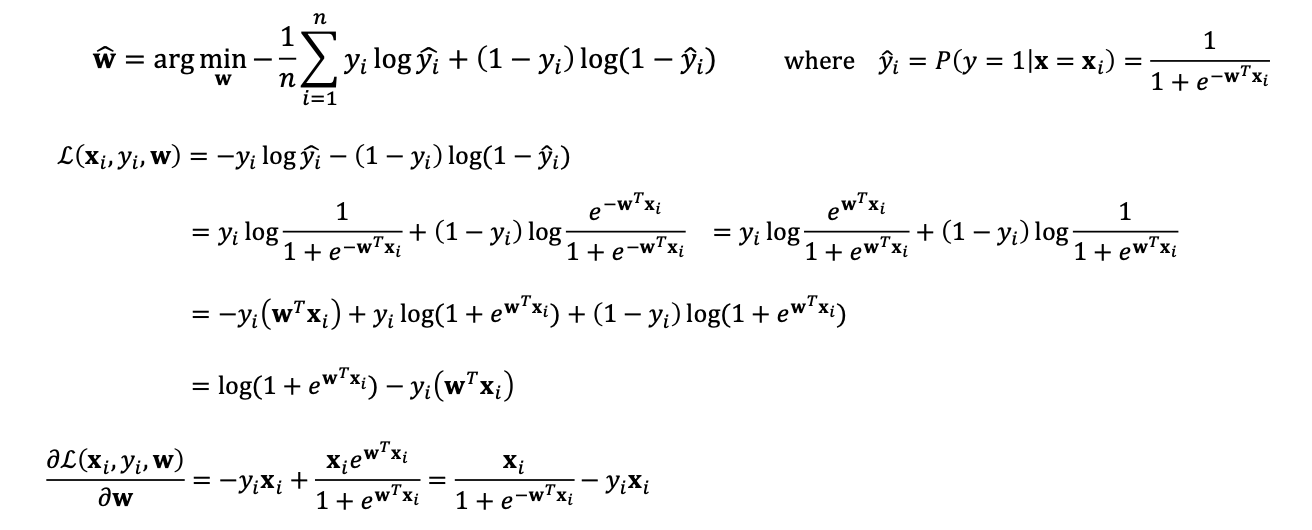
손실함수는 binary cross entropy입니다.

그리고 여기에서 아까 보았던 GD 알고리즘을 사용하면 됩니다!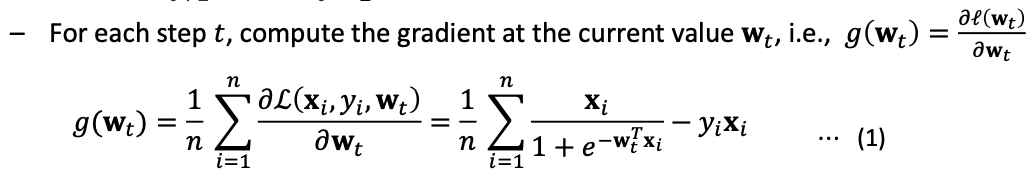

---

결론

많은 곳에서 사용하는 방법이니 잘 기억해두면 좋을 것 같네요

---

정리

참고자료 및 출처

https://www.youtube.com/playlist?list=PLl8OlHZGYOQ7bkVbuRthEsaLr7bONzbXS

https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote02_kNN.html

위 포스트는 코넬대학교 강의 CS4780과 그 강의 자료를 정리한 내용입니다.