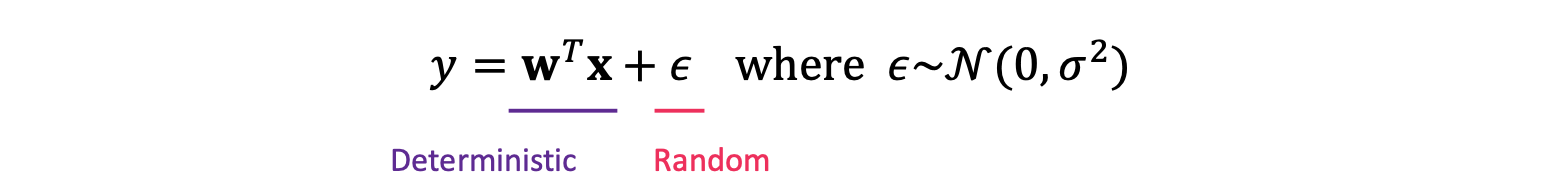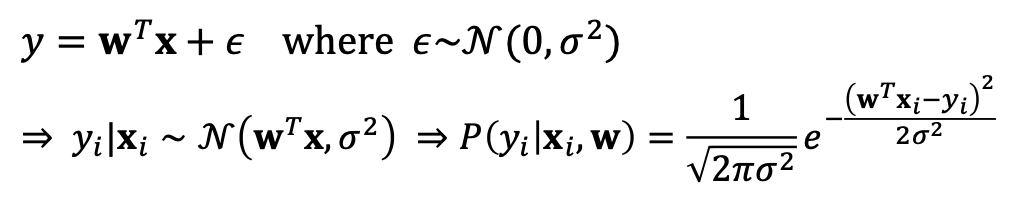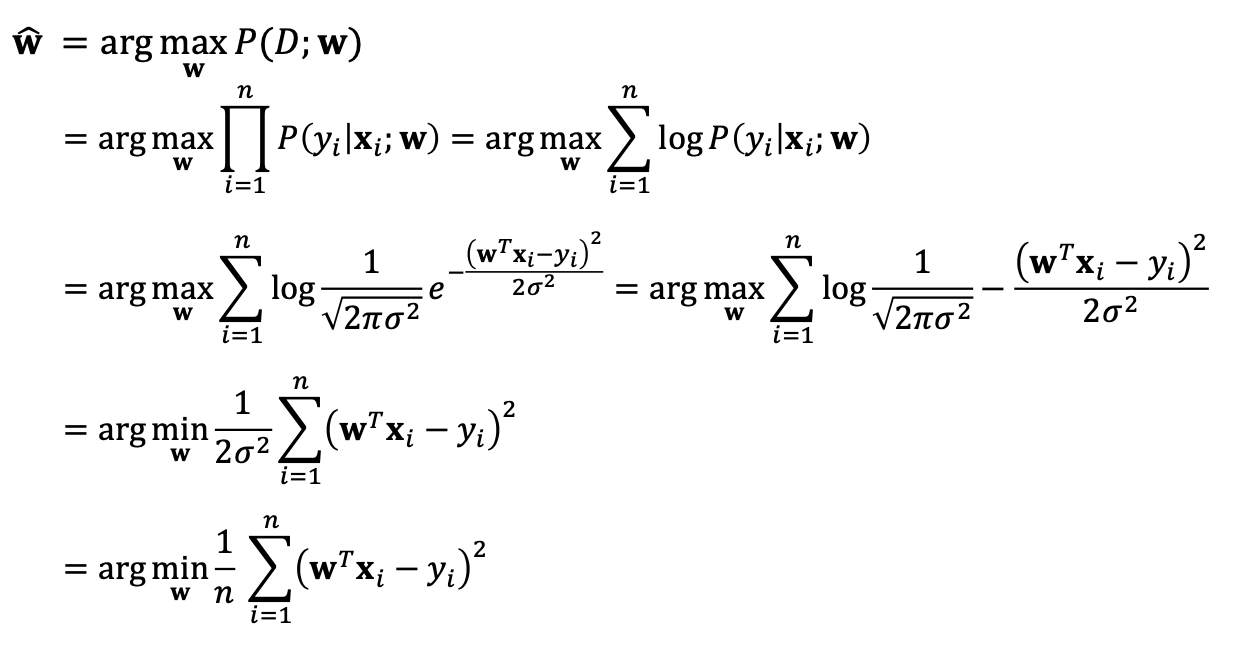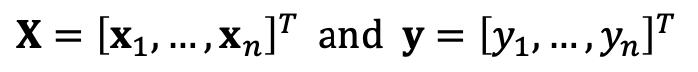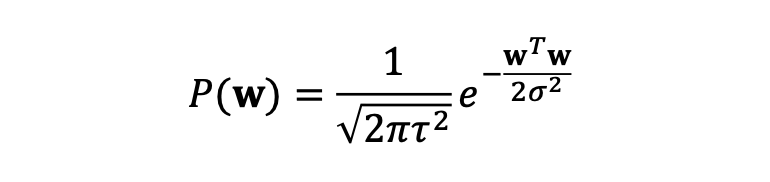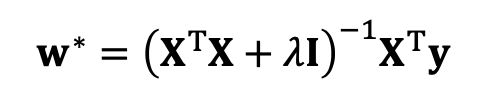Linear Regression, Ridge Regression
지능 시스템을 위한 기계학습
"기계학습"
"ML"
강의: CORNELL CS4780 "Machine Learning for Intelligent Systems"
해당 포스트는 코넬대학교 CS4780과 그 강의 자료를 정리한 내용입니다.
이 글을 쓰게 된 계기
기계학습에 대한 전반적인 이해와 그 알고리즘을 학습해봅시다!
So, what is Linear Regression, Ridge Regression?
데이터셋을 가장 잘 표현하는 직선을 그리는 문제입니다.
Linear Regression
선형 회귀, 회귀분석인만큼 대표하는 직선을 그리는 회귀분석입니다.
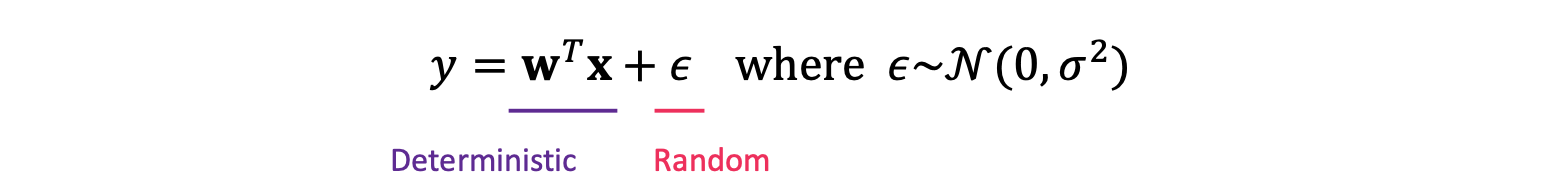
실제 관측값은 직선이 아닐 수 있습니다, 따라서 noise 를 추가하기도 합니다.
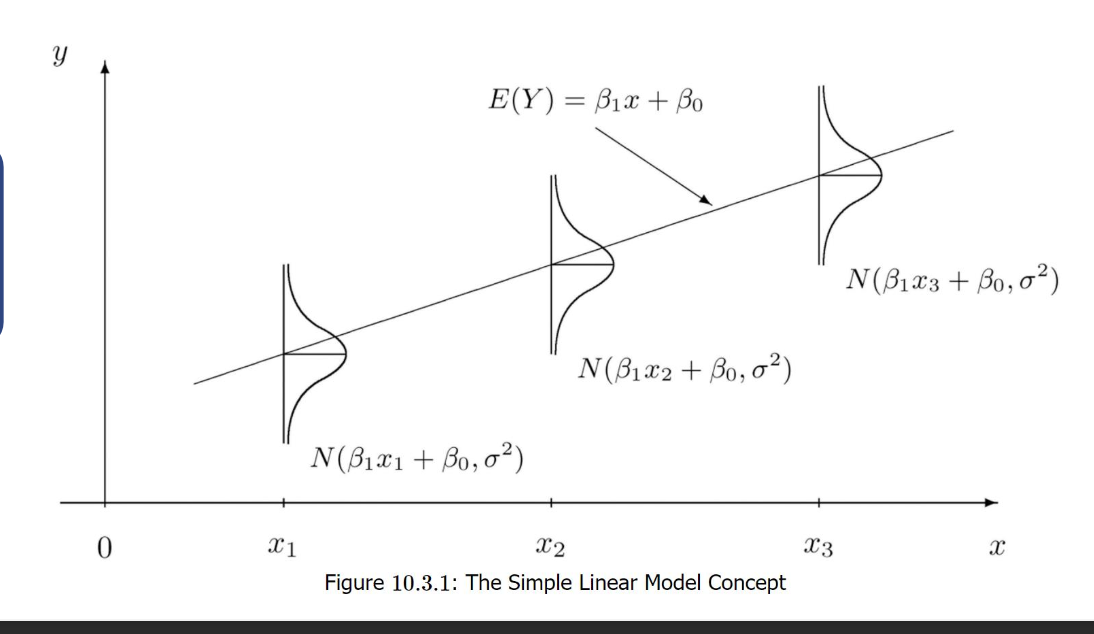
이런식으로 정규분포를 끼울 수 있습니다.
MLE를 위한 모델링과 수식전개를 해봅시다!
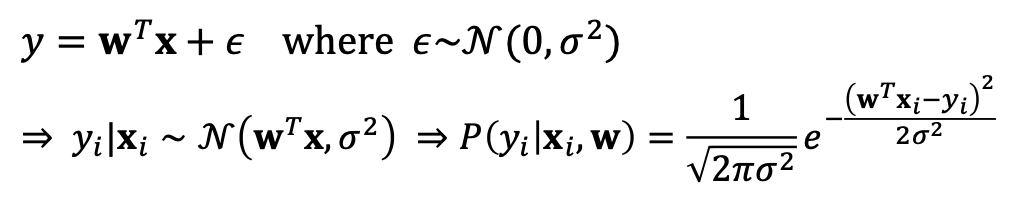
이런식으로 모델링을 해줍니다.
여기서 MLE를 적용해본다면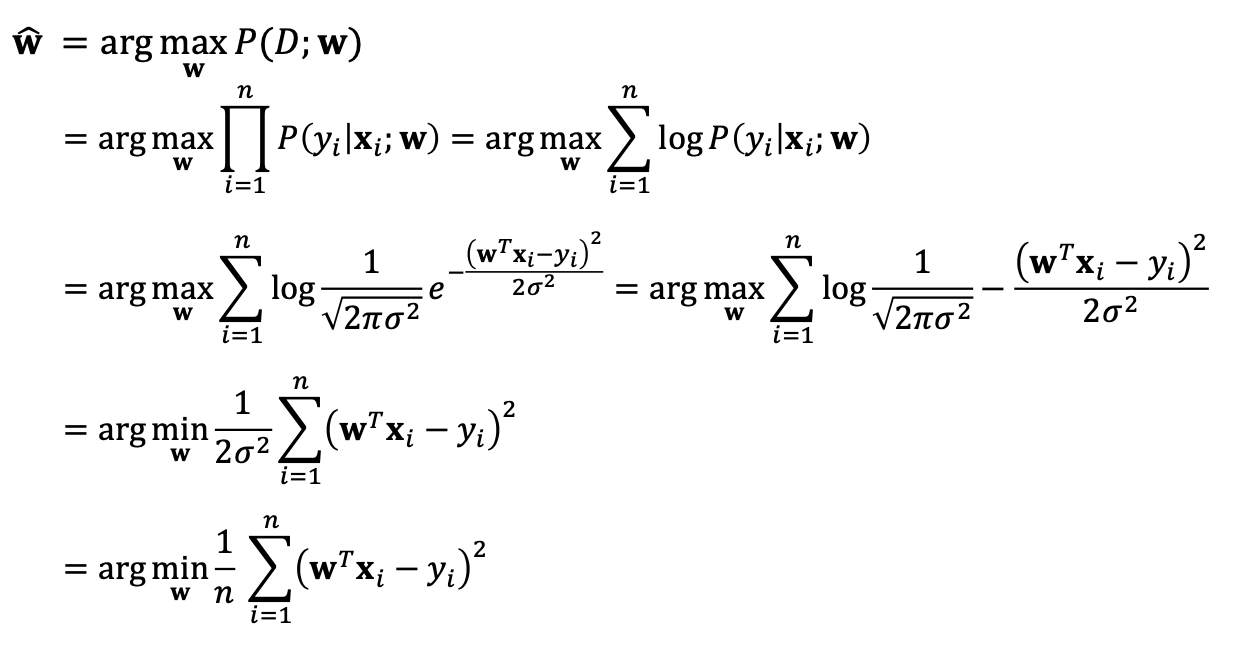
이렇게 수식이 전개가 되는건 놀라운 일이 아닙니다, 우리는 이 loss function을 최소화 해야합니다.
w∗=(XTX)−1XTy 로 쓸 수 있습니다.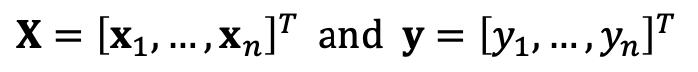
MAP도 적용해봅시다.
당연히 추가 가정이 필요합니다, prior를 추가합니다.
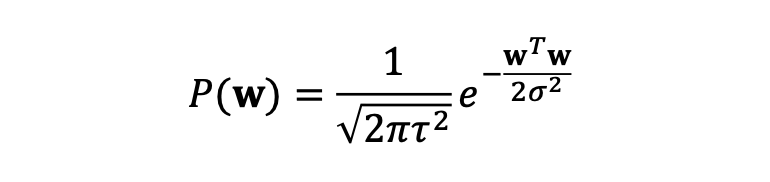
놀랄 필요 없습니다, 평균이 0이고, 분산이 τ2인 정규분포입니다.
이제 수식 전개가 가능합니다.

우리는 이것을 Ridge Regression이라고 부릅니다.
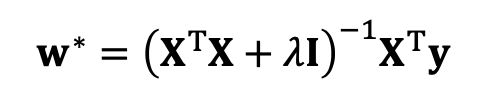
왜 why?
계산이 너무 방대해집니다...
우리는 경사하강법이라는 개쩌는 알고리즘을 쓸꺼에요.
정리
참고자료 및 출처
https://www.youtube.com/playlist?list=PLl8OlHZGYOQ7bkVbuRthEsaLr7bONzbXS
https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote02_kNN.html
위 포스트는 코넬대학교 강의 CS4780과 그 강의 자료를 정리한 내용입니다.