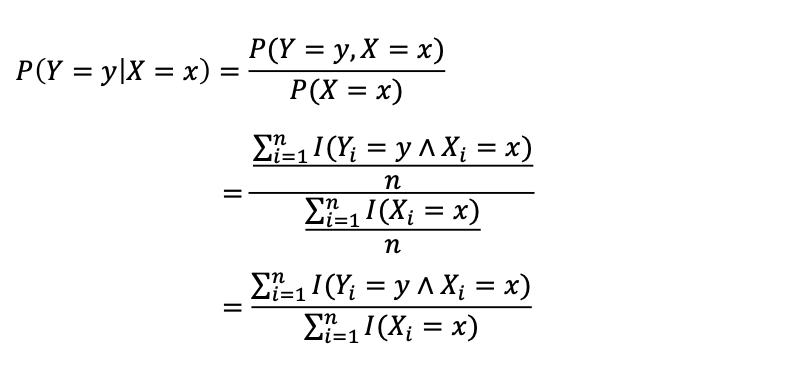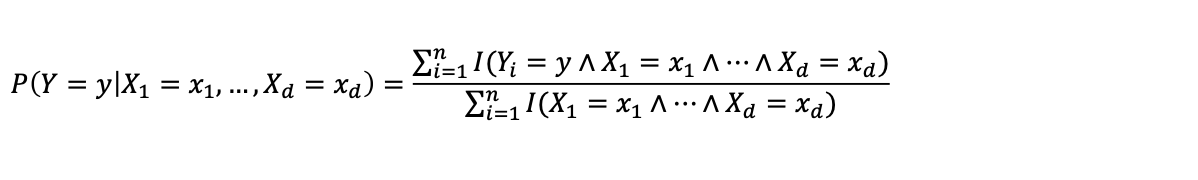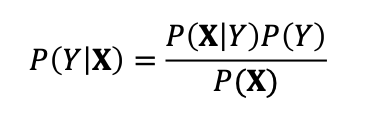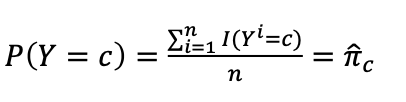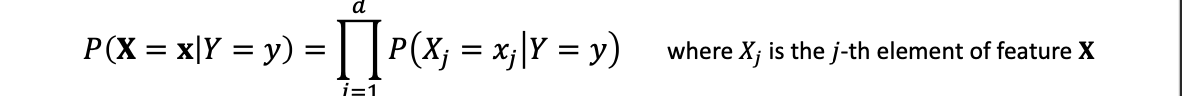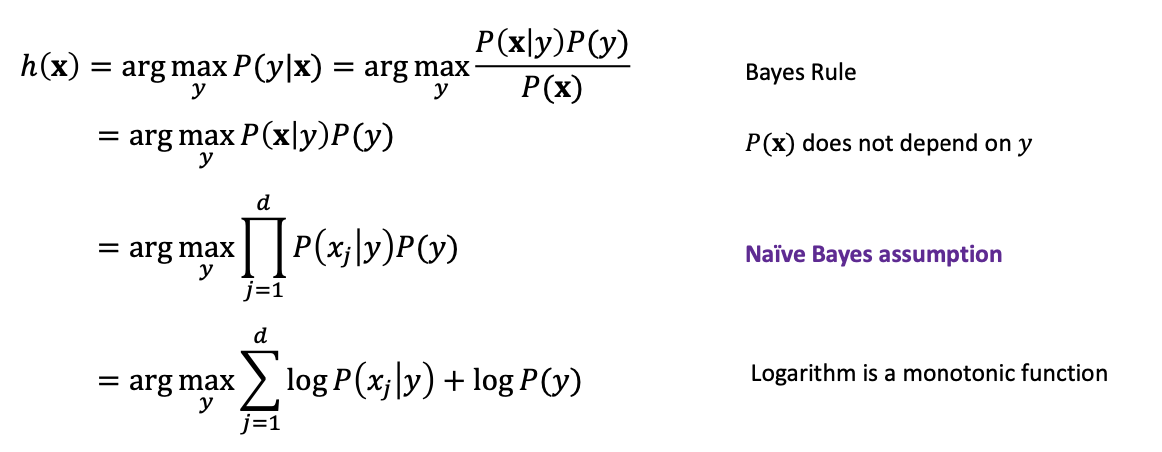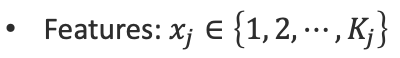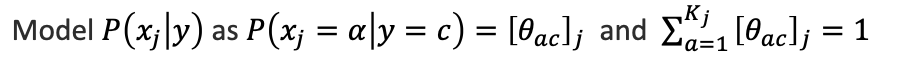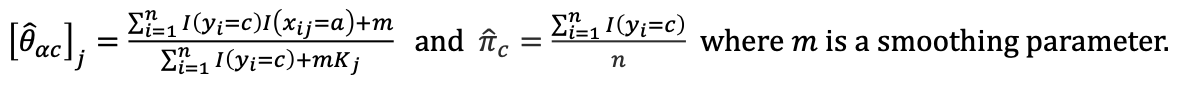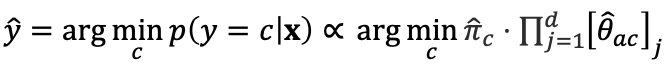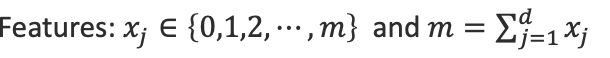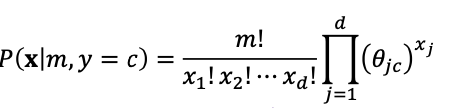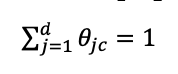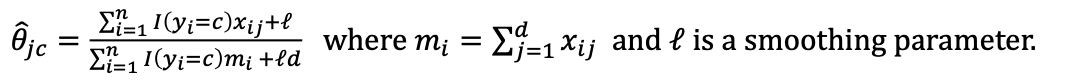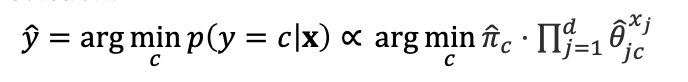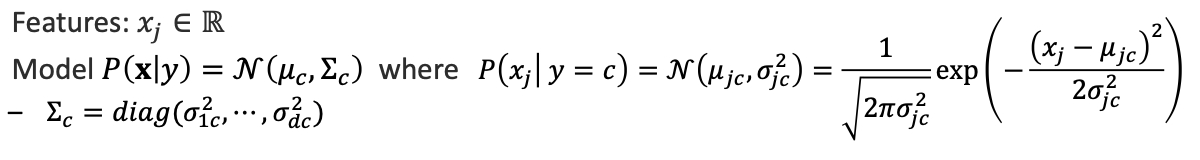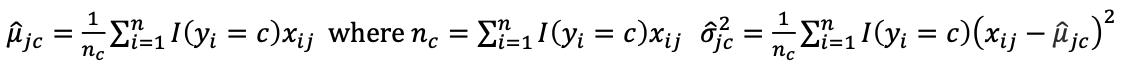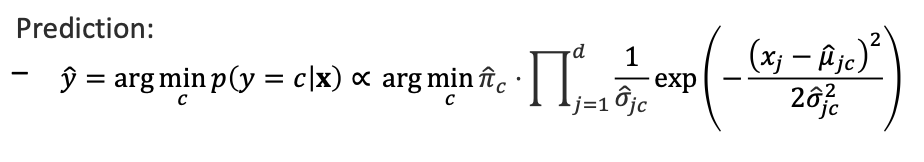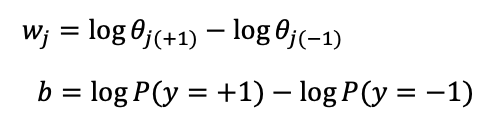Naïve Bayes Classifier

지능 시스템을 위한 기계학습

"기계학습"
"ML"
강의: CORNELL CS4780 "Machine Learning for Intelligent Systems"

해당 포스트는 코넬대학교 CS4780과 그 강의 자료를 정리한 내용입니다.

---

이 글을 쓰게 된 계기

기계학습에 대한 전반적인 이해와 그 알고리즘을 학습해봅시다!

---

So, what is Naïve Bayes Classifier?

천천히 알아가봅시다!

우리가 만약 𝐷 ∼ 𝑃(𝑌, 𝑋) 이러한 데이터를 갖고 있을 때 𝑃(𝑌 = 𝑦|𝑋 = 𝑥)은 어떻게 구해야 할까요?

간단한 solution

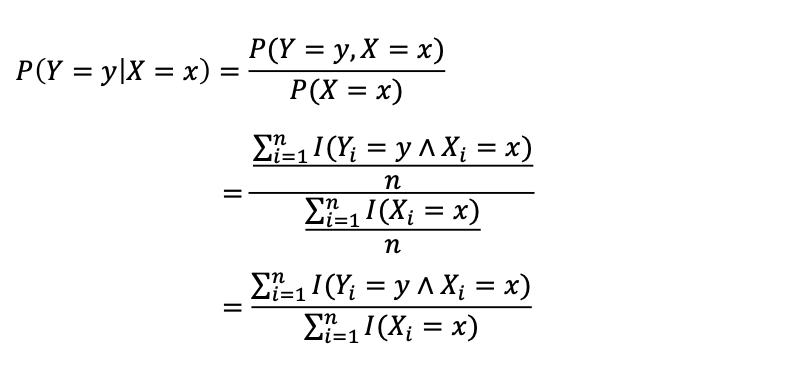
I는 true면 1을 뱉는다고 생각하셔도 좋습니다.

그렇다면 $𝐷 ∼ 𝑃(𝑌, 𝑋_1, … , 𝑋𝑑)$에서 $𝑃(𝑌 = 𝑦|𝑋_1 = 𝑥_1, … , 𝑋_𝑑 = 𝑥_𝑑)$는?

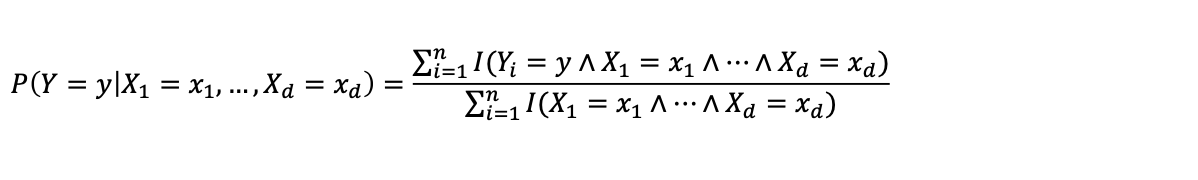
문제점

데이터의 차원이 커질수록 우리가 원하는 케이스는 드물어집니다.

결과적으로 좋지 않은 예측이 이루어집니다.

---

Solution, Naïve Bayes Classifier

추가적인 가정과 베이즈 정리를 통하여 해결해봅시다.

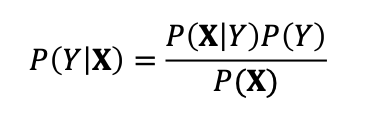
이 수식을 해결하기 위해 우리가 필요한 것은 $P(Y)$, 그리고 $P(\mathbf{X}|Y)$ 입니다.

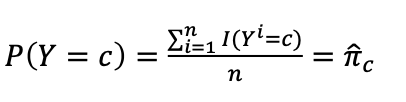
이것으로 전자를 가정해두고 후자는 Naïve Bayes assumption을 통하여 해결합시다.

Naïve Bayes assumption:

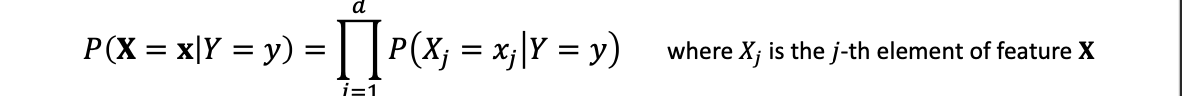
조건부 독립이라는 간단한 가정을 통해 우리는 식을 간단하게 만들 수 있습니다.

수식전개

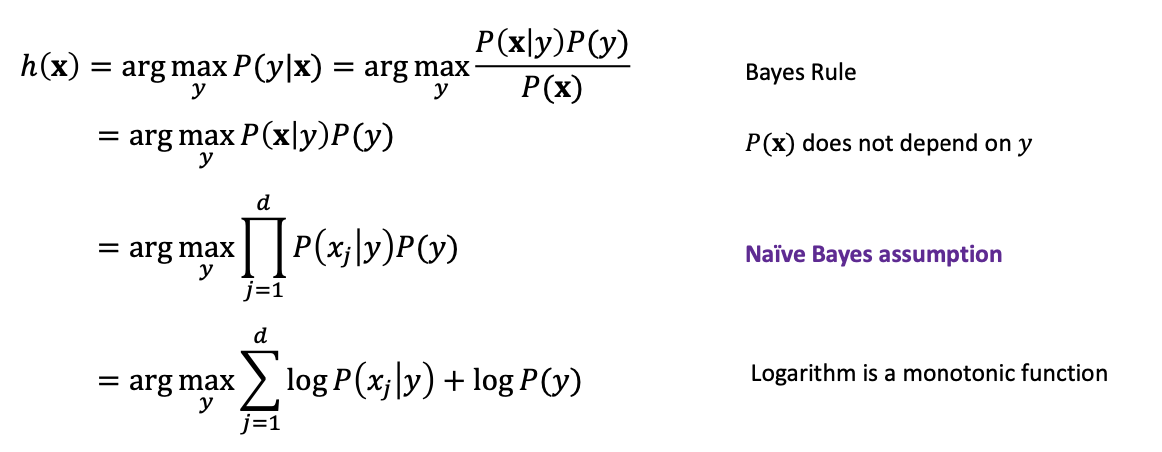
훨신 간단해진 수식을 볼 수 있습니다.

$P(x_j|y)$는 구하기 쉽기 때문입니다.

---

Three notable cases:

1. categorical features

핵심 부분

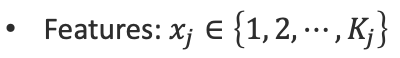
각각의 feature j 는 Kj의 카테고리중 하나로 떨어집니다.

---

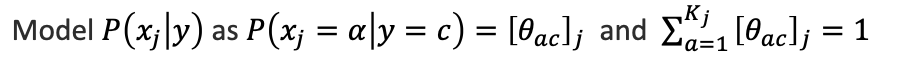
$[\theta_{\alpha c}]$ 는 특징 j가 라벨 c에 대하여 값 $\alpha$를 가짐을 의미합니다.

---

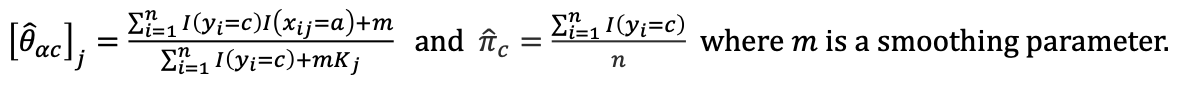
이렇게 추정 $\theta$를 구해주고

---

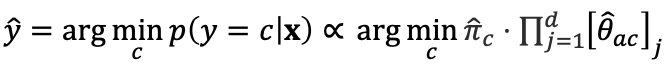
예측해주면 끝입니다.

2. multinomial features

핵심 부분

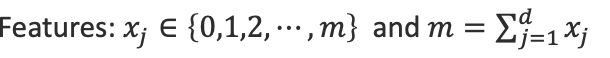
$x_j = a$ : j번째 element가 a번 나타남.

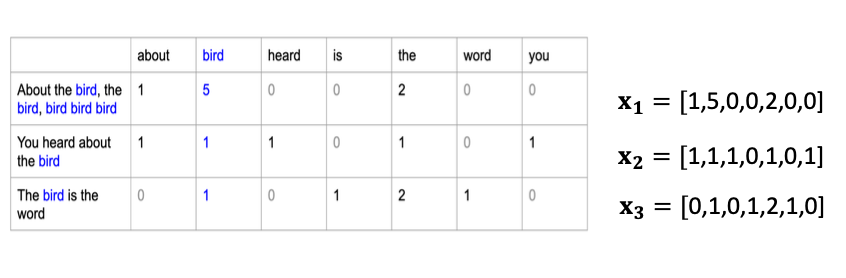
이 그림을 보면 이해가 쉬울 것 입니다!

---

그렇다면 수식을

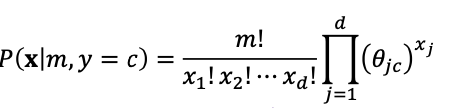
이렇게 세울 수 있습니다. 이때 우리는 순서를 신경쓰지 않을 것이므로 앞에 저런식으로 순서를 무시하기 위한 값을 곱해줍니다.

---

당연히

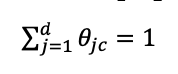
임을 잊지 말아야합니다.

---

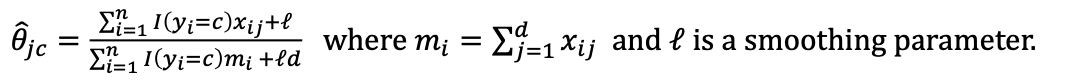
같은 방식으로 파라미터를 추정해주고

---

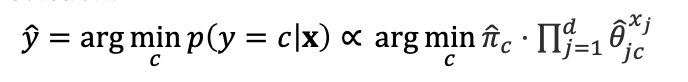
예측합니다. 이는 종종 스팸 메일 필터링에도 사용됩니다.

continuous features (Gaussian Naïve Bayes)

핵심부분

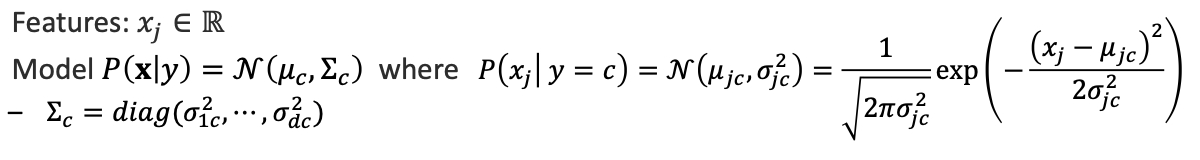
항상 하던 Feature 지정과 모델 선정입니다.

---

파라미터가 조금 생소할 수도 있지만

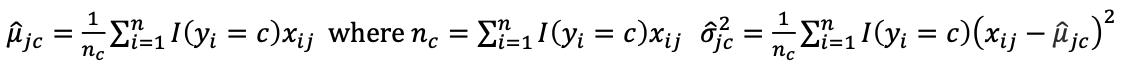
가우시안 분포의 파라미터를 구하면 됩니다.

---

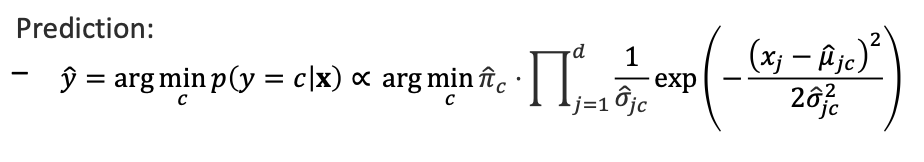
예측값도 이런 방식으로 구할 수 있습니다...

사실 나이브 베이즈 분류기는 linear decision으로 이어질 수 있습니다.

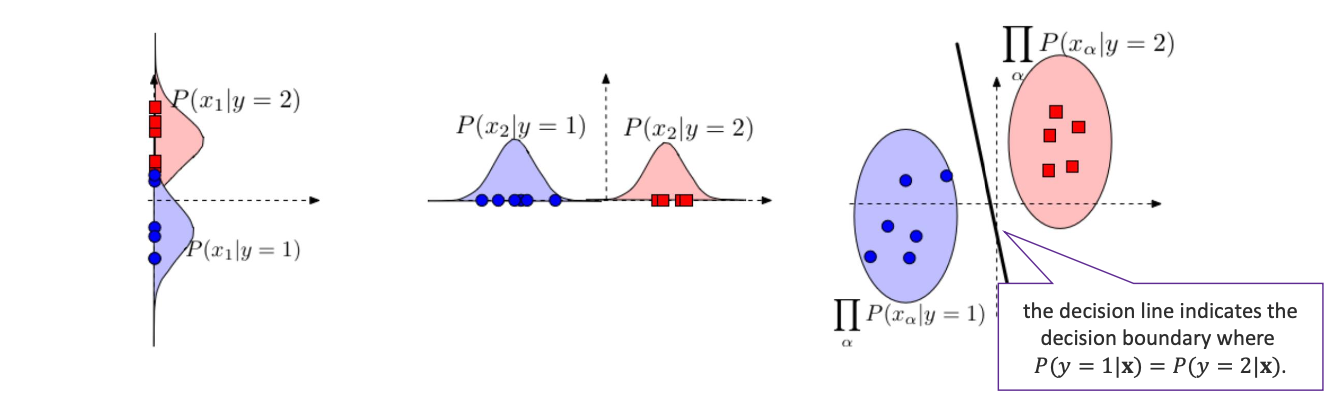
위에서 보았던 연속적인 경우에서도 우리는 이렇게 결정 Line을 그리는 것을 볼 수 있습니다.

수식 전개

우리는 $𝑦_𝑖 = −1 \text{ or } 1$과 feature are multinomial 임을 가정하고 시작해봅시다.

목표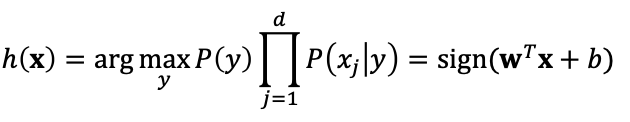 임을 증명.

---

증명

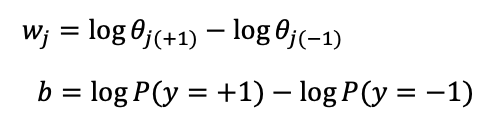
따라서 초평면을 구하는 linear classificaion과 유사하다고 볼 수 있습니다!

---

결론

많은 곳에서 사용하는 방법이니 잘 기억해두면 좋을 것 같네요

---

정리

참고자료 및 출처

https://www.youtube.com/playlist?list=PLl8OlHZGYOQ7bkVbuRthEsaLr7bONzbXS

https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote02_kNN.html

위 포스트는 코넬대학교 강의 CS4780과 그 강의 자료를 정리한 내용입니다.