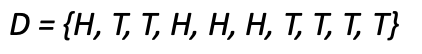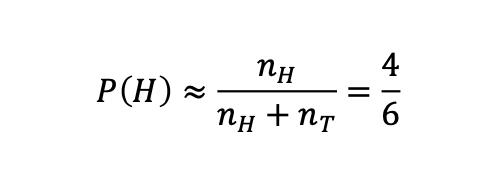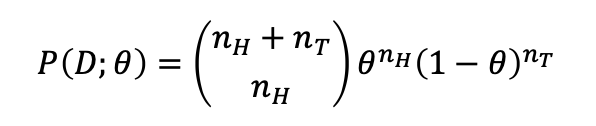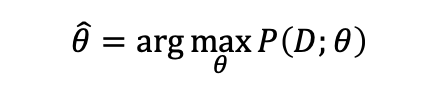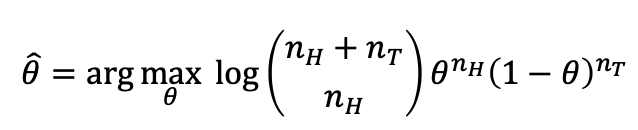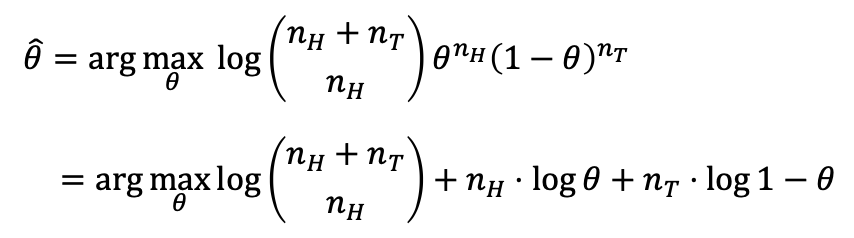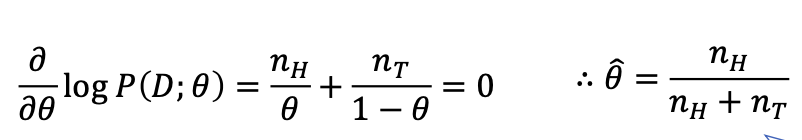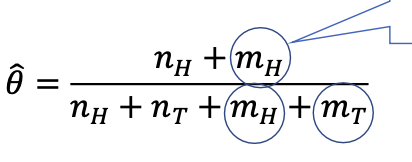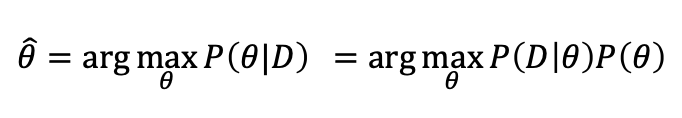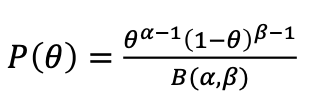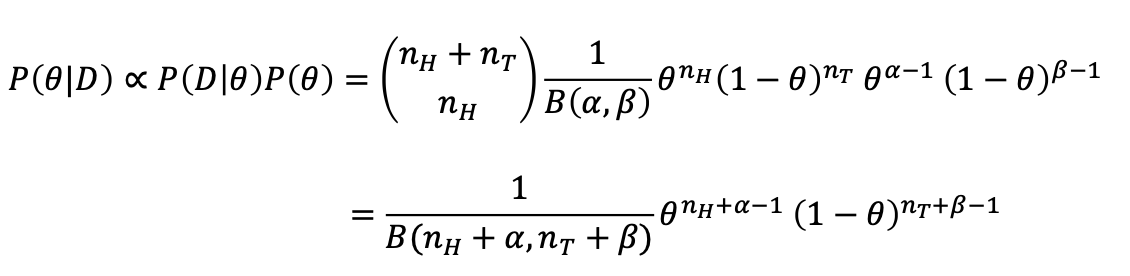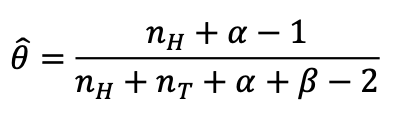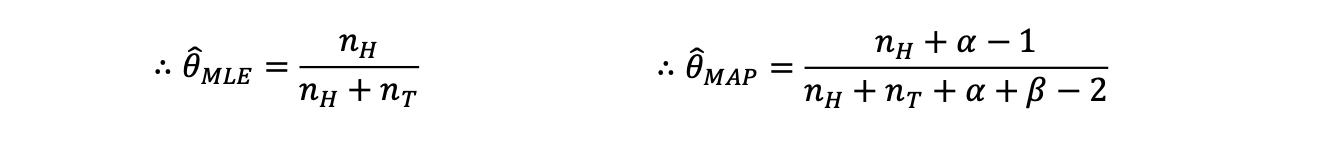
MLE, MAP

지능 시스템을 위한 기계학습

"기계학습"
"ML"
강의: CORNELL CS4780 "Machine Learning for Intelligent Systems"

해당 포스트는 코넬대학교 CS4780과 그 강의 자료를 정리한 내용입니다.

---

이 글을 쓰게 된 계기

기계학습에 대한 전반적인 이해와 그 알고리즘을 학습해봅시다!

---

So, what is MLE, MAP?

MLE : Maximum Likelihood Estimation

MAP: Maximum a Priori Estimation

우리의 직관을 컴퓨터가 이해할 수 있을까요?

당연히 아니라고 생각할 수 있습니다.

이러한 데이터셋이 주어졌을때 앞면이 나올 확률, 즉 P(H)는 어떻게 구해야할까요?

---

우리의 직관으로는

이렇게 수식을 전개할 수 있습니다만... 컴퓨터는 이러한 직관을 아직 갖지 못했습니다.

해결책?

그렇다면 이것을 어떤 방식으로 해결해야할까요?

Solution : MLE

우리는 파라미터 𝜃 가 주어졌을때 데이터셋이 나올 확률을 𝑃(𝐷;𝜃)이라고 두고 최댓값을 구합니다. (MLE)

P(D;𝜃)의 분포를 가정합니다 (binomial distribution)

확률은 최대가 되어야 합니다.

가정(모델링)과 위의 수식을 통해

우리는 𝜃에 대한 추정값인 theta hat을 구할 수 있습니다. 로그는 왜 있을까요..?

수식을 풀어봅시다.

자 이제 로그가 사용된 이유가 나타납니다, 계산이 매우 간단해졌습니다.

신기하게도 우리의 직관과 같은 결과가 나왔습니다.

주의

MLE는 직관을 구현하는것이 아닙니다, 용어의 편의를 위해 직관이라는 단어를 사용했지만 직관과 유사한 결과를 낳는다는 것을 보여주기 위함입니다.

---

그러나 우리는 동전을 던지면 반반의 확률을 갖는다는 믿음(혹은 사전 지식)이 있습니다, 이것은 어떻게 적용할까요?

$m_H , m_T$를 추가(Hallucinating)함으로서 우리의 믿음을 적용해볼 수 있습니다.

이는 smoothing이라고도 불립니다.

구현방법은 무엇일까요?

Bayesian Approach

Frequentist vs Bayesian

둘의 가장 큰 차이는 $\theta$를 최적화할 파라미터로 보는지(MLE) or 확률변수로 보는지(MAP)에 달려있습니다.

먼저, 용어정리 해야겠죠.

기억해둡시다.

MAP 수식 전개

베이즈 정리를 이용할 수 있습니다.

그리고 P(𝜃)가 베타분포를 따른다고 가정합시다.

그렇다면 우리는 이런식으로 수식을 전개할 수 있습니다!

똑같이 argmax 𝜃를 씌우고 미분을 통해 추정 𝜃를 구하면

우리의 사전지식이 담긴 추정 𝜃를 구할 수 있습니다.

값이 매우 커지면 Hallucinationg이 의미가 없어집니다.

---

결론

은 Naive bayes에서...

정리

참고자료 및 출처

https://www.youtube.com/playlist?list=PLl8OlHZGYOQ7bkVbuRthEsaLr7bONzbXS

https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote02_kNN.html

위 포스트는 코넬대학교 강의 CS4780과 그 강의 자료를 정리한 내용입니다.