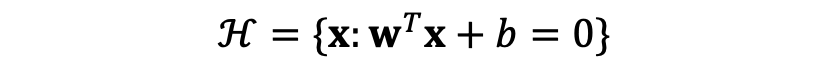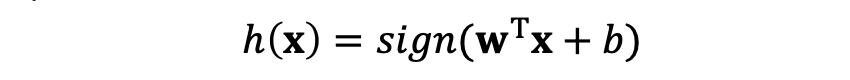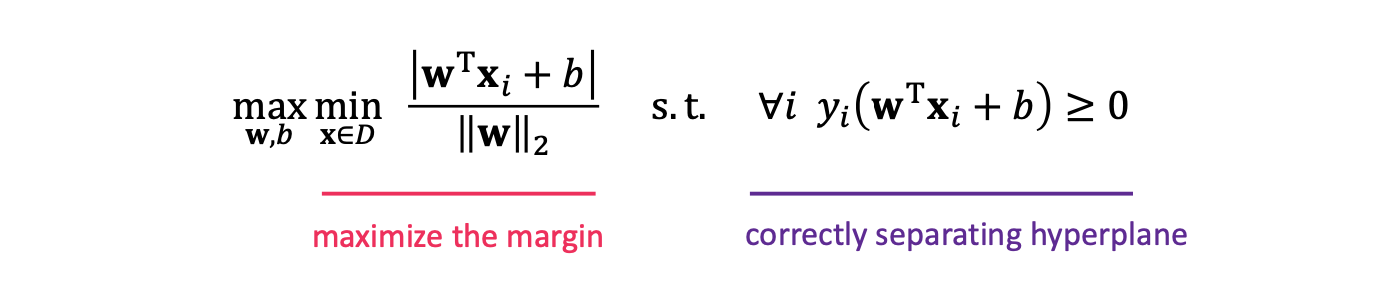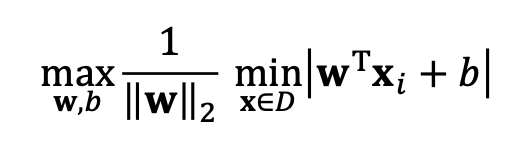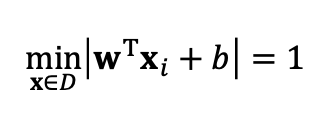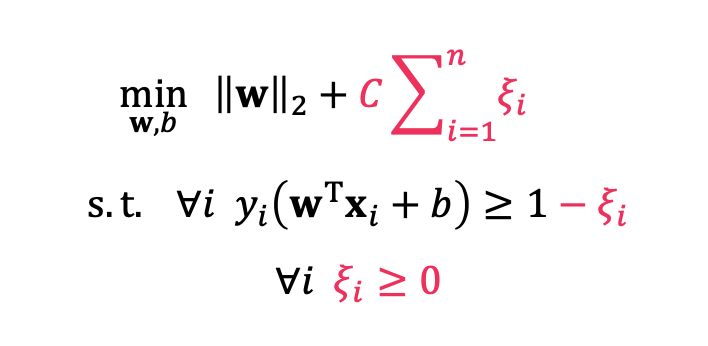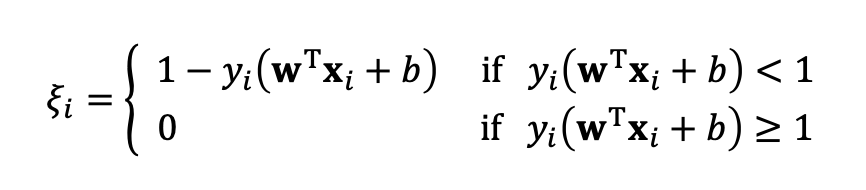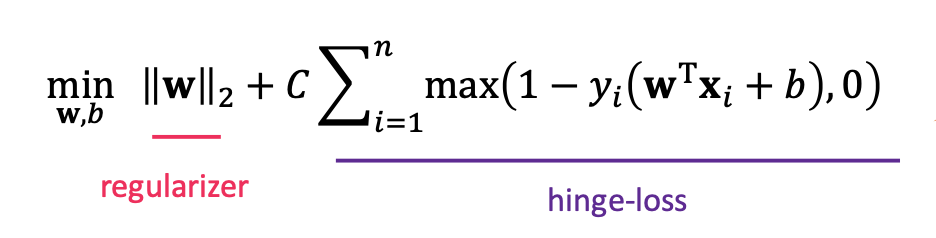SVM: Support Vector Machine

지능 시스템을 위한 기계학습

"기계학습"
"ML"
강의: CORNELL CS4780 "Machine Learning for Intelligent Systems"

해당 포스트는 코넬대학교 CS4780과 그 강의 자료를 정리한 내용입니다.

---

이 글을 쓰게 된 계기

기계학습에 대한 전반적인 이해와 그 알고리즘을 학습해봅시다!

---

So, what is SVM: Support Vector Machine?

알아봅시다!

SVM은 결국 직선 긋기 입니다.

초기 가정

이진 분류가 가능해야합니다, i.e. $y = -1 \text{ or } +1$ and linearly separable.

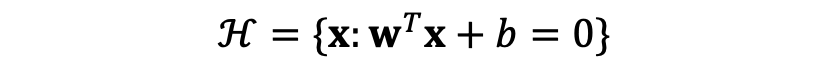
똑같이 초평면을 구하기 위해 class를 하나 설정해줍시다. 그렇다면 우리는 perceptron과 같이

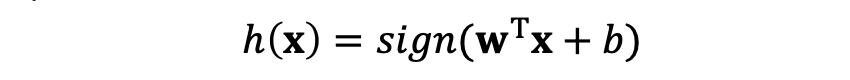
이런 분류기를 얻어야 함이 저희의 목표입니다...만

그렇다면 perceptron과 다른것이 무엇인가요?

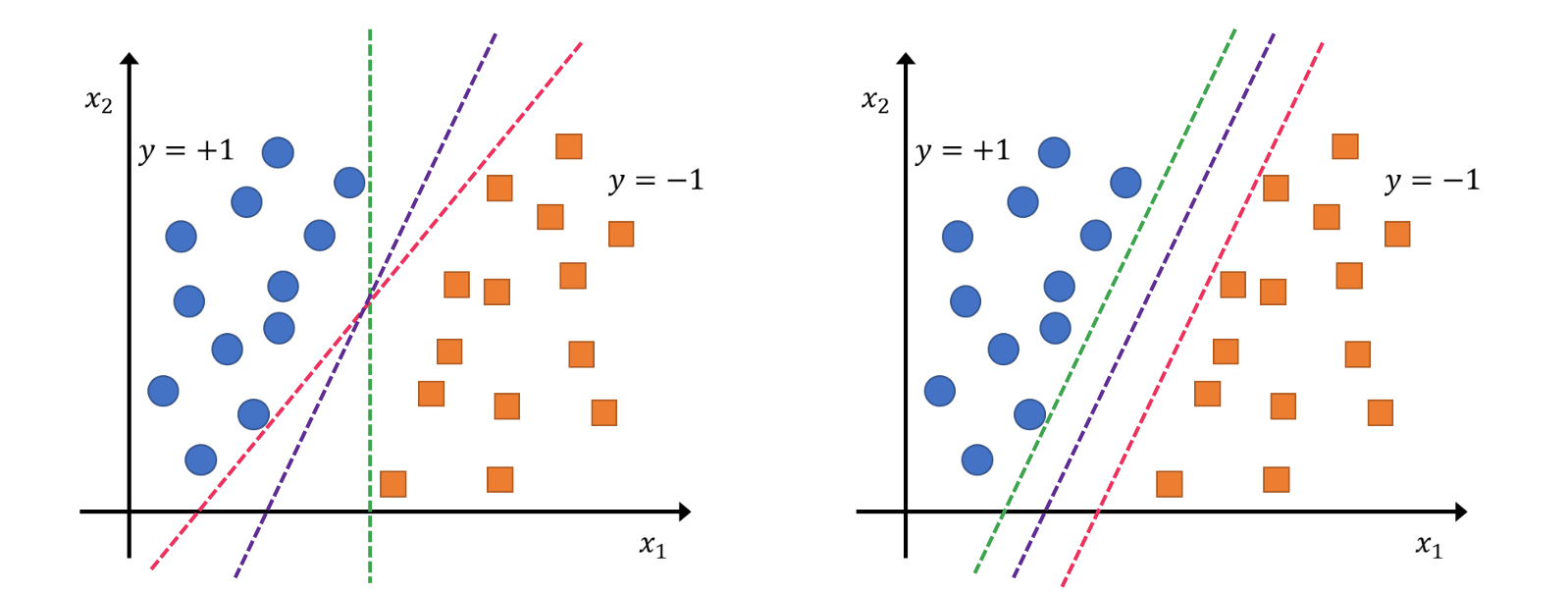
우리는 직관적으로 Margin이 최대가 되는 것을 원합니다, 즉 각각의 클래스의 초평면과 가장 가까운점 x와 초평면과의 거리가 가능한 한 최대가 되는 것을 원하는 것 입니다.

Margin을 조금 더 엄밀하게 바라봅시다.

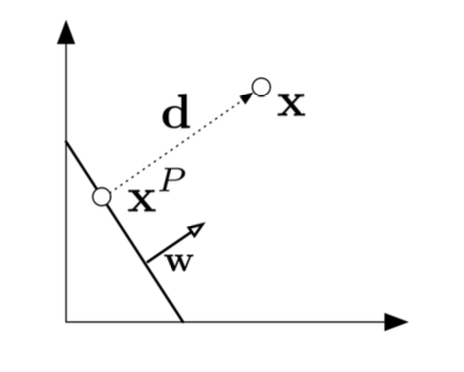
$\mathbf{b}$ 는 $H$에서 $\mathbf{x}$까지의 최단거리입니다. 이것은 margin이 될 수 있습니다.

$\mathbf{x}^p$를 $H$로의 $\mathbf{x}$의 사영이라고 가정합시다.

위의 두 수식으로 인하여 $\mathbf{x}^p = \mathbf{x}-\mathbf{d}$임을 알 수 있고 $\mathbf{d} = a\mathbf{w}$임을 알 수 있습니다 (d가 w의 스칼라배)

또한 $\mathbf{x}^p∈ H$ 는 $\mathbf{w}^T\mathbf{x}^p + b = 0$ 임 을 의미합니다.

따라서

$\mathbf{w}^T\mathbf{x}^p + b = \mathbf{w}^T(\mathbf{x}-\mathbf{d}) + b =\mathbf{w}^T(\mathbf{x}-a\mathbf{w}) + b = 0$

이고, 이는 곧 $a = \frac{w^T x + b}{w^T w}$ 으로 이어집니다.

그리고 d의 길이 는

$\|\mathbf{d}\|_2 = \sqrt{\mathbf{d}^T \mathbf{d}} = \sqrt{\alpha^2 \mathbf{w}^T \mathbf{w}} = \frac{|\mathbf{w}^T \mathbf{x} + b|}{\sqrt{\mathbf{w}^T \mathbf{w}}} = \frac{|\mathbf{w}^T \mathbf{x} + b|}{\|\mathbf{w}\|_2}$ 으로 정리할 수 있습니다 따라서

Margin of $\mathcal{H} \text{ w.r.t } D: \gamma(\mathbf{w}, b) = \min_{\mathbf{x} \in D} \frac{|\mathbf{w}^T \mathbf{x} + b|}{\|\mathbf{w}\|_2}$ 라는 것을 얻을 수 있습니다!

이를 이용하여 constrained optimization problem을 지켜봅시다.

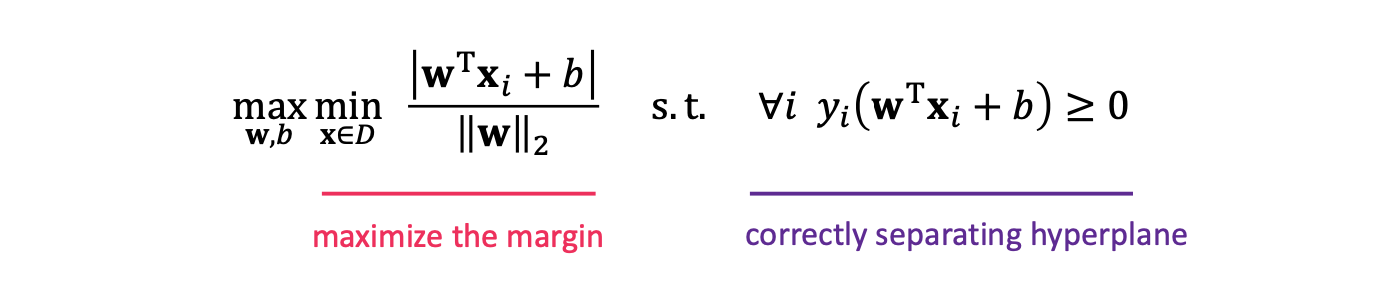
여기에서 좌측이 목적 함수이고, 우측이 제약 조건 입니다. 목적은 margin 최대화이고, 제약은 올바른 분류입니다.

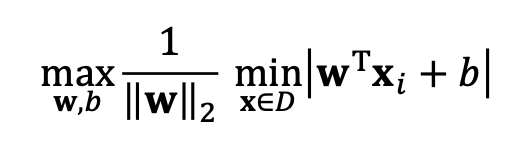
식을 이렇게 분리하고 w와 b를 rescaling 합시다.

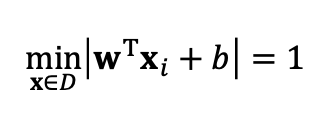
이 과정을 통해 우리는

이것임을 알 수 있습니다.

Support Vectors:

우리는 위 식을 통하여 $y_i(\mathbf{w}^T\mathbf{x}_i +b) = 1$인 training point가 필요합니다, 그리고 우리는 이것을 support vectors라고 부르겠습니다.

얘네들이 바로 최대 margin 점들이 됩니다. 따라서 이 점들이 없어지거나 바뀌지 않는 이상 SVM또한 바뀌지 않습니다.

약한 규제?

만약 최대 마진을 통해 해결책을 얻지 못한다면...(ex 저차원 데이터)

규제를 약하게 해야합니다. 따라서 우리는

slack variables ($\xi_i$)를 집어넣어 약하게 간섭해봅시다.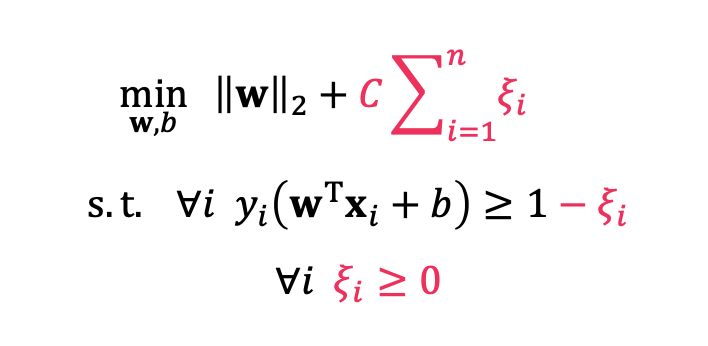

제약조건과 규제가 약간 바뀌었습니다.

이를 통해 input x가 hyperplane에 조금 더 가까이 다가갈 수 있게 해줍니다. 만약 C가 너무 작다면 규제가 매우 느슨해지며, 간단한 해결책으로 인해 몇개의 point들을 버려야 합니다.

---

여전히 convex한 이 문제를 해결하기 위해서는 우리는 제약 조건을 slack 변수에 넣어서 제거해보는 하나의 방법을 생각해볼 수 있습니다.

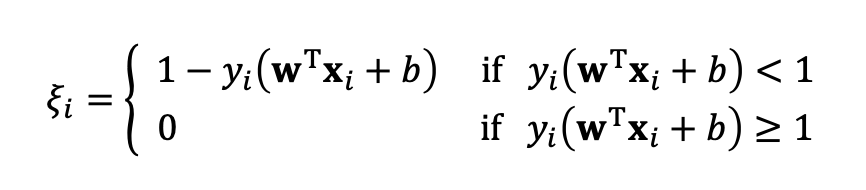
이러한 방법으로 slack 변수를 설정하면 매우 작은 값으로 유지가 가능합니다, 또한 필요한 경우에만 적용이 가능합니다.

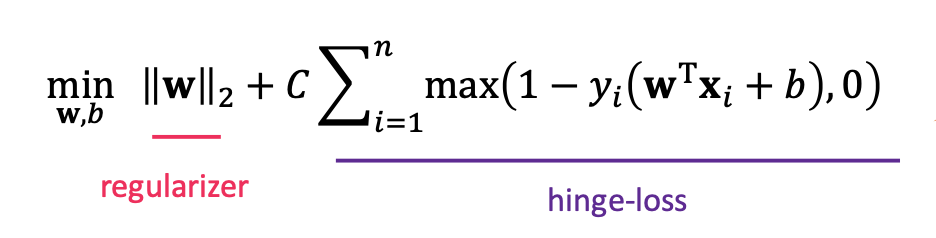
결과적으로 이러한 수식을 얻을 수 있고, 이는 logistic regression과 유사하네요.

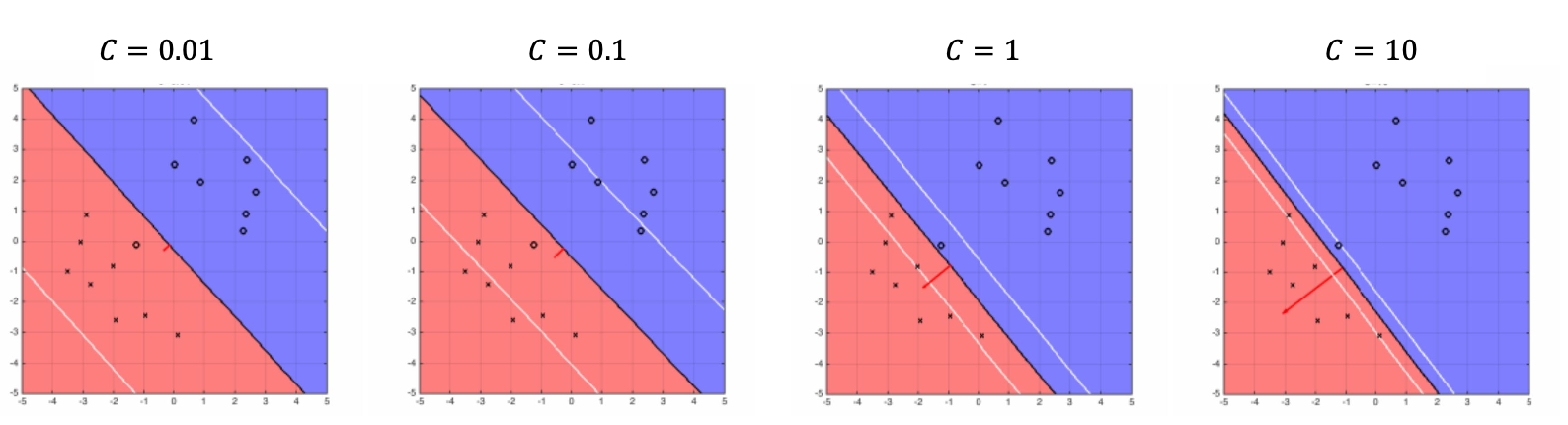
참고자료, C값에 따른 변화를 보여줍니다

정리

야무지네요...

참고자료 및 출처

https://www.youtube.com/playlist?list=PLl8OlHZGYOQ7bkVbuRthEsaLr7bONzbXS

https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote02_kNN.html

위 포스트는 코넬대학교 강의 CS4780과 그 강의 자료를 정리한 내용입니다.