🙆🏻‍♀️ 요긴하게 쓰일 template

int binary_search(...) {
    while (left < right) {
        mid = left + (right - left) / 2;
        if (condition(...)) {
            right = mid;
        } else {
            left = mid + 1;    
        }
    }
    return left
}

loop가 종료된 뒤 lo는 condition()을 만족하는 가장 작은 값이 된다!!

---

💡 Search in Rotated Sorted Array

There is an integer array nums sorted in ascending order (with distinct values).

Prior to being passed to your function, nums is possibly rotated at an unknown pivot index k (1 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].

Given the array nums after the possible rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.

You must write an algorithm with O(log n) runtime complexity.

Example 1:

Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4

Example 2:

Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1

Example 3:

Input: nums = [1], target = 0
Output: -1

Constraints:

• 1 <= nums.length <= 5000
• -104 <= nums[i] <= 104
• All values of nums are unique.
• nums is an ascending array that is possibly rotated.
• -104 <= target <= 104

Solution

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int low = 0;
        int high = nums.size() - 1;

        while (low <= high) {
            int mid = low + ((high - low) / 2);

            if (target == nums[mid]) {
                return mid;
            } else {
                if (nums[low] <= nums[mid]) { 
                    //mid number belongs to the left portion
                    if (nums[low] <= target && target < nums[mid]) {
                        // if the target number is in the range of the left portion
                        //   only perform the search on the left portion
                        high = mid - 1;
                    } else {
                        // the target number is (maybe) in the right portion
                        low = mid + 1;
                    }
                } else { // nums[mid] <= nums[high]
                    // mid number belongs to the right portion
                    if (nums[mid] < target && target <= nums[high]) {
                        // if the target number is in the range of the right portion
                        //   only perform the search on the right portion
                        low = mid + 1;
                    } else {
                        // the target number is (maybe) in the left portion
                        high = mid - 1;
                    }
                }
            }
        }

        // when here, there is no target number in the nums array
        return -1;
    }
};

---

💡 Find Minimum in Rotated Sorted Array

Suppose an array of length n sorted in ascending order is rotated between 1 and n times. For example, the array nums = [0,1,2,4,5,6,7] might become:

• [4,5,6,7,0,1,2] if it was rotated 4 times.
• [0,1,2,4,5,6,7] if it was rotated 7 times.

Notice that rotating an array [a[0], a[1], a[2], ..., a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], ..., a[n-2]].

Given the sorted rotated array nums of unique elements, return the minimum element of this array.

You must write an algorithm that runs in O(log n) time.

Example 1:

Input: nums = [3,4,5,1,2]
Output: 1
Explanation: The original array was [1,2,3,4,5] rotated 3 times.

Example 2:

Input: nums = [4,5,6,7,0,1,2]
Output: 0
Explanation: The original array was [0,1,2,4,5,6,7] and it was rotated 4 times.

Example 3:

Input: nums = [11,13,15,17]
Output: 11
Explanation: The original array was [11,13,15,17] and it was rotated 4 times. 

Constraints:

• n == nums.length
• 1 <= n <= 5000
• -5000 <= nums[i] <= 5000
• All the integers of nums are unique.
• nums is sorted and rotated between 1 and n times.

Solution

일단 내가 짠 코드는 이렇다

class Solution {
public:
    int findMin(vector<int>& nums) {
        int low = 0;
        int high = nums.size() - 1;

        int result = 0;

        while (low <= high) {
            int mid = low + ((high - low) / 2);

            if (nums[low] <= nums[high]) {
                // sorted in our current window
                result = nums[low];
                break;
            }

            if (nums[low] <= nums[mid]) {
                // the minimum number is in the right portion
                low = mid + 1;
            } else {
                // the minimum number is in the left portion
                // for the case when the nums has odd number of elements,
                //  we need to include the mid number as part of the left portion
                high = mid;
            }
        } 

        return result;
    }
};

최소 숫자가 right portion에 있는지, left portion에 있는지 판단할 때,
nums[low] <= nums[mid] 를 사용했다

근데 이 컨디션을 비슷한듯 다른
nums[mid] > nums[high] 로 바꿔주면 더욱 간단한 코드로 짤 수 있다

class Solution {
public:
    int findMin(vector<int>& nums) {
        int low = 0;
        int high = nums.size() - 1;

        int result = 0;

        while (low < high) {
            int mid = low + ((high - low) / 2);

            if (nums[mid] > nums[high]) {
                // the minimum number is in the right portion
                low = mid + 1;
            } else {
                // the minimum number is in the left portion
                // for the case when the nums has odd number of elements,
                //  we need to include the mid number as part of the left portion
                high = mid;
            }
        } 

        return nums[low];
    }
};

왜 이렇게 될까?

.. 생각해보자

nums[low] <= nums[mid] 이 컨디션으로 판단한다면

• 지금 내가 보고있는 window가 전체적으로 sorted 된건지
• 아니면 first half만 sorted 된건지

이렇게 두가지의 경우가 나올 수 있다
그래서 loop을 돌면서 한번더 확인해줘야 하는 번거로움이 생겼다

하지만 nums[mid] > nums[high] 컨디션으로 판단한다면

• 일단 가운데 값이 맨끝 값보다 크기 때문에 현재 window는 sorted가 아님을 확신할 수 있다
• second half에 최소 숫자가 있다

이렇게 second half에 최소 숫자가 있다고 확신할 수 있게 되어
extra condition이 필요 없게된다

---

💡 Search Insert Position

Given a sorted array of distinct integers and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order.

You must write an algorithm with O(log n) runtime complexity.

Example 1:

Input: nums = [1,3,5,6], target = 5
Output: 2

Example 2:

Input: nums = [1,3,5,6], target = 2
Output: 1

Example 3:

Input: nums = [1,3,5,6], target = 7
Output: 4

Constraints:

• 1 <= nums.length <= 104
• -104 <= nums[i] <= 104
• nums contains distinct values sorted in ascending order.
  --104 <= target <= 104

Solution

이거 약간 헷갈리는게,,

target 숫자가 nums에 없으면 그냥 lo를 return하는게,,,,

while 컨디션이 lo <= hi 라서, lo가 hi와 같아질때 까지 게속 루프를 돌텐데
lo와 hi가 같아지는 순간에는 mid도 lo와 hi와 같은 값이다
이때 else if 구문의 condition에서 target 숫자를 오른쪽에 넣을건지, 왼쪽에 넣을건지 판단할 수 있게 된다!!
→ element가 한개인 array를 생각해보자

nums = [2], target=1
nums = [2], target=3

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int result = 0;

        int lo = 0;
        int hi = nums.size() - 1;

        while (lo <= hi) {
            int mid = lo + ((hi - lo) / 2);

            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] < target) {
                lo = mid + 1;
            } else {
                hi = mid - 1;
            }
        }

        return lo;
    }
};

---

💡Capacity To Ship Packages Within D Days

A conveyor belt has packages that must be shipped from one port to another within days days.

The ith package on the conveyor belt has a weight of weights[i]. Each day, we load the ship with packages on the conveyor belt (in the order given by weights). We may not load more weight than the maximum weight capacity of the ship.

Return the least weight capacity of the ship that will result in all the packages on the conveyor belt being shipped within days days.

Example 1:

Input: weights = [1,2,3,4,5,6,7,8,9,10], days = 5
Output: 15
Explanation: A ship capacity of 15 is the minimum to ship all the packages in 5 days like this:
1st day: 1, 2, 3, 4, 5
2nd day: 6, 7
3rd day: 8
4th day: 9
5th day: 10

Note that the cargo must be shipped in the order given, so using a ship of capacity 14 and splitting the packages into parts like (2, 3, 4, 5), (1, 6, 7), (8), (9), (10) is not allowed.

Example 2:

Input: weights = [3,2,2,4,1,4], days = 3
Output: 6
Explanation: A ship capacity of 6 is the minimum to ship all the packages in 3 days like this:
1st day: 3, 2
2nd day: 2, 4
3rd day: 1, 4
Example 3:

Input: weights = [1,2,3,1,1], days = 4
Output: 3
Explanation:
1st day: 1
2nd day: 2
3rd day: 3
4th day: 1, 1

Constraints:

• 1 <= days <= weights.length <= 5 * 104
• 1 <= weights[i] <= 500

Solution

이거 개어렵네,,

일단 해답의 lower bound와 upper bound를 생각해보자
lower bound는 maximum element이고
uppderbound는 total sum of the array이다

이제 binary search의 개념을 [lowerbound, upperboud]에 도입해보자

• capacity(mid)가 너무 작아서 days보다 더 자주 보내야 한다면
  → 더 큰 capacity를 찾으러 떠나자!
• capacity(mid)가 너무 커서 days보다 더 적게 보내야 한다면
  → 더 작은 capacity를 찾으러 떠나자!
• days에 딱 맞게 떨어지는 capacity(mid)를 찾았다면
  → 더 작은 capacity를 찾으러 떠나자!

class Solution {
    bool condition(vector<int>& weights, int capacity, int target_days) {
        // capacity가 주어졌을때, weight를 capacity로 나눠서 보냈을 때:
        //  - days가 target_days보다 많다면 return false (더 많은 capacity로 보내도 된다)
        //  - days가 target_days보다 적거나 같다면 return true (더 적은 capacity로 쪼개서 보내야 한다 / 더 작은 값이 있을 수도 있다)
        int days = 1;
        int sum = 0;
        for (int i = 0; i < weights.size(); i++) {
            sum += weights[i];
            if (sum > capacity) {
                // 더 담을 수 없다 -> 보내야 한다
                days++;
                sum = weights[i]; //계산 다시 시작!
            }
        }

        if (days > target_days) {
            // days가 충분하다
            return false;
        }
        // days가 부족하다
        return true;
    }

public:
    int shipWithinDays(vector<int>& weights, int days) {
        // 먼저 range를 찾기 위해 다음을 계산해준다
        int lo = *max_element(weights.begin(), weights.end()); 
        int hi = accumulate(weights.begin(), weights.end(), 0);

        while (lo < hi) {
            int mid = lo + ((hi - lo) / 2);
            if (condition(weights, mid, days)) {
                hi = mid;
            } else {
                lo = mid + 1;
            }
        }

        // according to binary template
        //  loop가 종료되면 lo는 condition()을 만족하는 가장 작은 값이 된다
        return lo;
    }
};

---

💡 Search a 2D Matrix

Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:

Integers in each row are sorted from left to right.
The first integer of each row is greater than the last integer of the previous row.

Example 1:

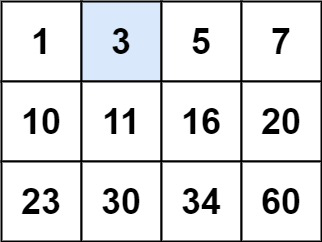
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

Solution

가로, 세로가 각각 sorted이니깐

세로 먼저 binary search 해서 row#을 찾고 그 row에 binary search를 하면 되겠다

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int lowRow = 0;
        int highRow = matrix.size() - 1;
        
        while (lowRow < highRow) {
            int mid = lowRow + (highRow - lowRow) / 2;
            if (matrix[mid][0] == target) {
                return true;
            }
            if (matrix[mid][0] < target && target < matrix[mid + 1][0]) {
                // row를 찾음!
                lowRow = mid;
                break;
            }
            if (matrix[mid][0] < target) {
                lowRow = mid + 1;
            } else {
                highRow = mid - 1;
            }
        }
        
        int lowCol = 0;
        int highCol = matrix[0].size() - 1;
        
        while (lowCol <= highCol) {
            int mid = lowCol + (highCol - lowCol) / 2;
            if (matrix[lowRow][mid] == target) {
                return true;
            }
            if (matrix[lowRow][mid] < target) {
                lowCol = mid + 1;
            } else {
                highCol = mid - 1;
            }
        }
        
        return false;
    }
};

matrix의 특징을 활용해 좀 더 efficient한 코드로 짜보자면

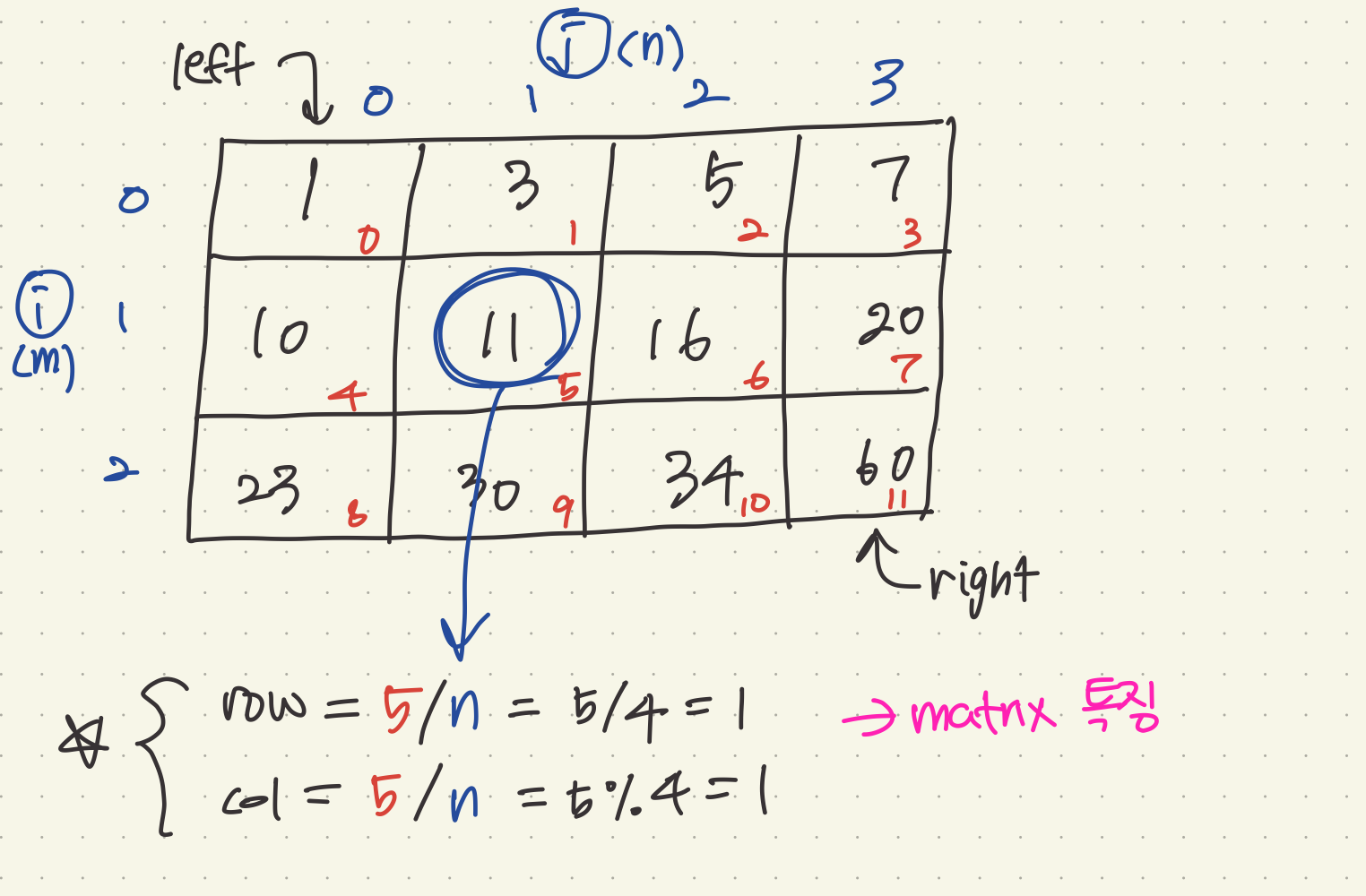
class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {

        int left = 0;
        int m = matrix.size();
        int n = matrix[0].size();
        int right = m * n - 1;

        while (left <= right){

            int middle = right + (left - right) / 2;

            // compute sub-indices using matrix structure
            int row = middle / n;
            int col = middle % n; 


            //ordinary binary search
            int middle_x = matrix[row][col];
            if (target > middle_x){
                left = ++middle;
            } else if (target < middle_x){
                right = --middle;
            } else {
                return true;
            }


        }

        return false;
        
    }
};

---

💡 Koko Eating Bananas

Koko loves to eat bananas. There are n piles of bananas, the ith pile has piles[i] bananas. The guards have gone and will come back in h hours.

Koko can decide her bananas-per-hour eating speed of k. Each hour, she chooses some pile of bananas and eats k bananas from that pile. If the pile has less than k bananas, she eats all of them instead and will not eat any more bananas during this hour.

Koko likes to eat slowly but still wants to finish eating all the bananas before the guards return.

Return the minimum integer k such that she can eat all the bananas within h hours.

Example 1:

Input: piles = [3,6,7,11], h = 8
Output: 4

Example 2:

Input: piles = [30,11,23,4,20], h = 5
Output: 30

Example 3:

Input: piles = [30,11,23,4,20], h = 6
Output: 23

Solution

class Solution {
public:
    int minEatingSpeed(vector<int>& piles, int h) {
        int n = piles.size();
        
        // [1, max(piles)]에 binary search를 하면서 찾는다!
        int low = 1;
        int high = 0;
        for (int i = 0; i < n; i++) {
            // 한번에 최대로 먹을 수 있는 amount는 max(piles)이다
            high = max(high, piles[i]);
        }
        
        int result = high; // we are trying to find the minimum
        
        // binary search!  
        while (low <= high) { //O(log m)
            int k = low + (high - low) / 2;
            long int hours = 0;
            for (int i = 0; i < n; i++) { //O(n)
                // 한번에 k만큼씩 먹는다고 할 때 몇시간이 걸리는지 계산
                hours += ceil((double) piles[i] / k);
            }
            if (hours <= h) {
                // if you can eat in h hours with eating speed of k,
                // then store this amount if this is the minimum
                // and keep on search for more minimum k
                result = min(result, k);
                high = k - 1;
            } else {
                // if you exceed h hours with eating speed of k,
                // then you need to enhance the eating speed! eat faster!! 
                low = k + 1;
            }
        } //O(n * log m)
        
        return result;
    }
};