💡 Subsets

Given an integer array nums of unique elements, return all possible
subsets.

The solution set must not contain duplicate subsets. Return the solution in any order.

Example 1:

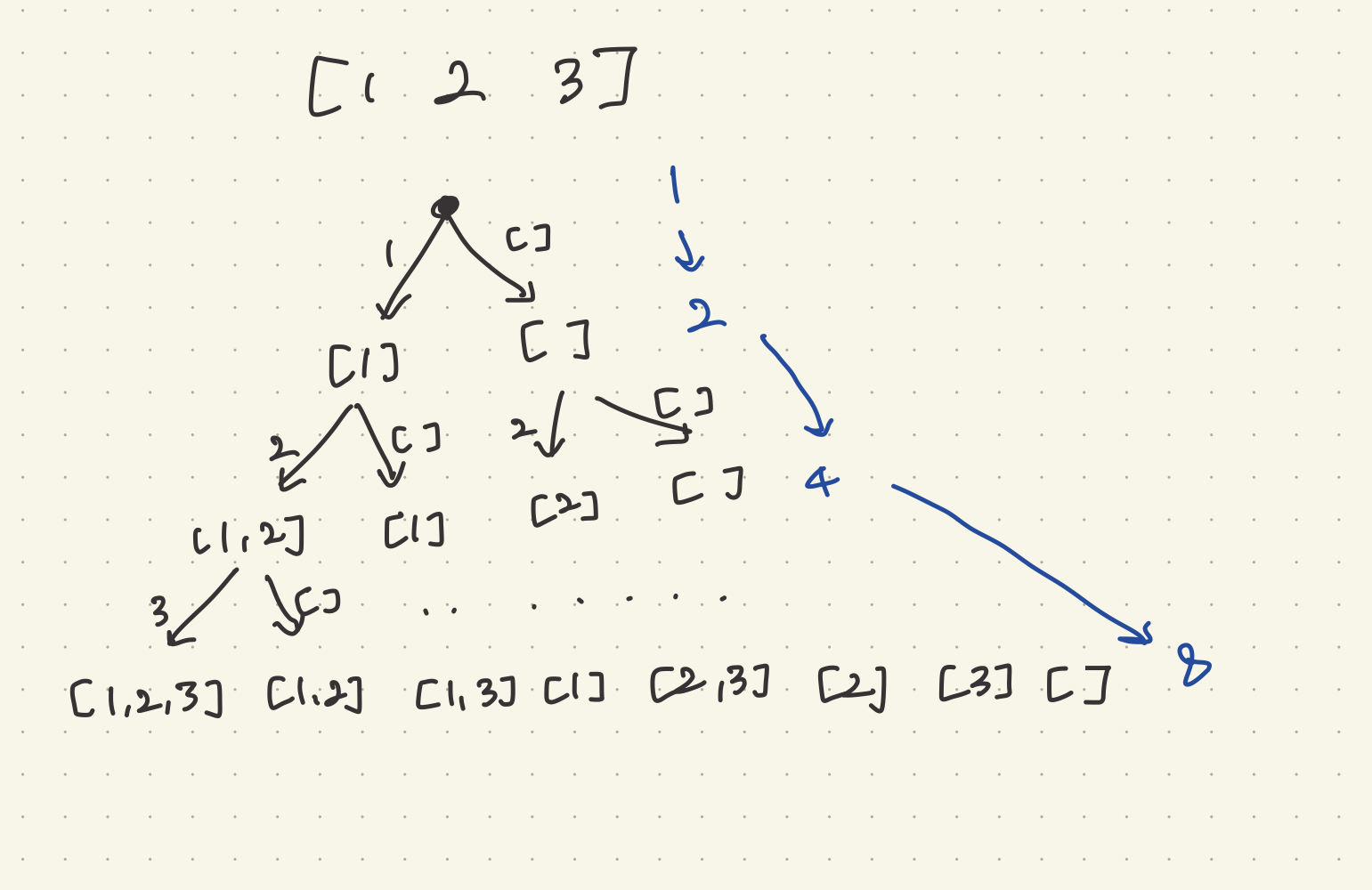
Input: nums = [1,2,3]
Output: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

Example 2:

Input: nums = [0]
Output: [[],[0]]

Solution

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> result;

        vector<int> subset; // current subset
        dfs(nums, 0, subset, result);
        return result;
    }
private:
    void dfs(vector<int> &nums, int i, vector<int> &subset, vector<vector<int>> &result) {
        if (i >= nums.size()) {
            result.push_back(subset);
            return;
        }

        // decision to include nums[i]
        subset.push_back(nums[i]);
        dfs(nums, i+1, subset, result);

        // decision NOT to include nums[i]
        subset.pop_back();
        dfs(nums, i+1, subset, result);
    }
};

---

💡 Combination Sum

Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order.

The same number may be chosen from candidates an unlimited number of times. Two combinations are unique if the
frequency of at least one of the chosen numbers is different.

The test cases are generated such that the number of unique combinations that sum up to target is less than 150 combinations for the given input.

Example 1:

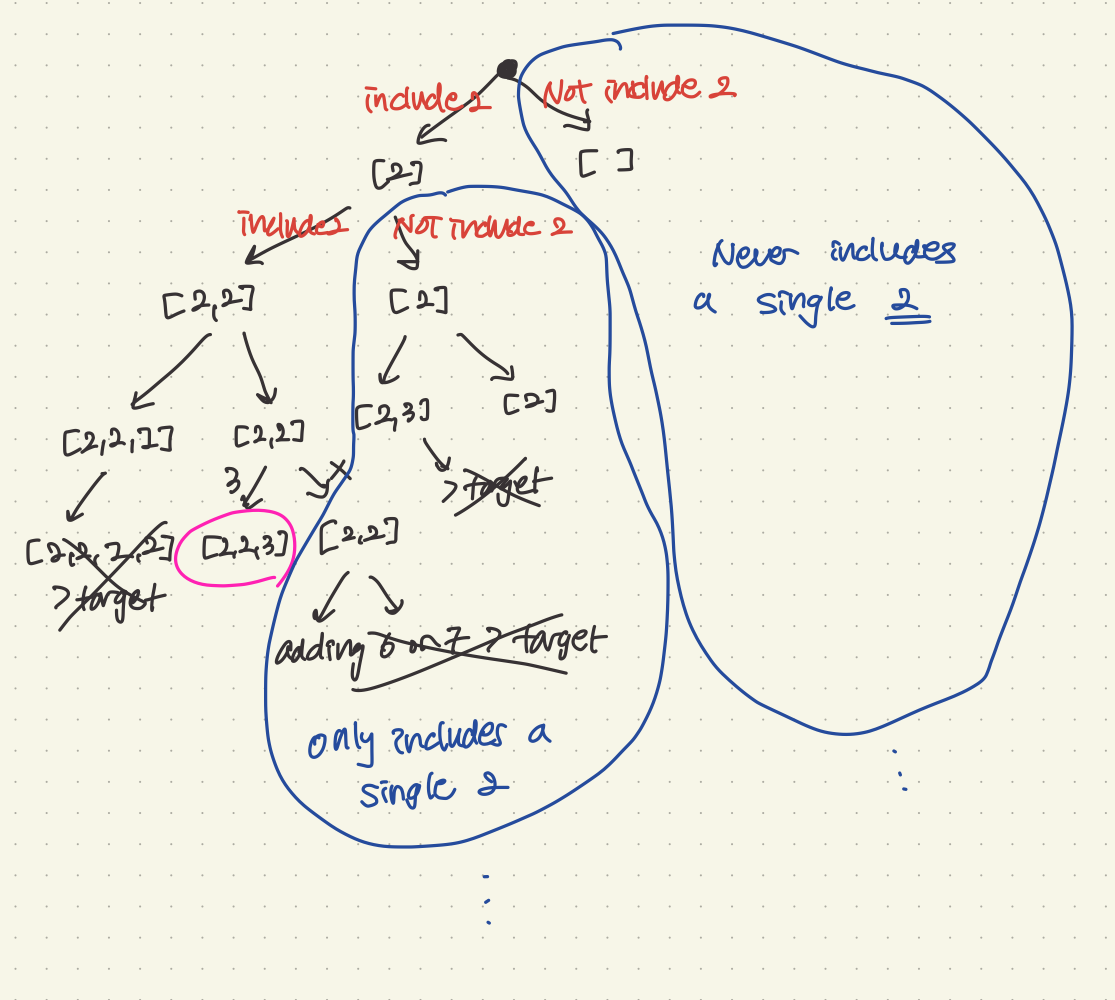
Input: candidates = [2,3,6,7], target = 7
Output: [[2,2,3],[7]]
Explanation:
2 and 3 are candidates, and 2 + 2 + 3 = 7. Note that 2 can be used multiple times.
7 is a candidate, and 7 = 7.
These are the only two combinations.

Example 2:

Input: candidates = [2,3,5], target = 8
Output: [[2,2,2,2],[2,3,3],[3,5]]

Example 3:

Input: candidates = [2], target = 1
Output: []

Solution

class Solution {
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<vector<int>> result;

        vector<int> combination;
        dfs(candidates, target, 0, 0, combination, result);
        return result;
    }
private:
    void dfs(vector<int> &candidates, int target, int i, int sum, vector<int> &combination, vector<vector<int>> &result) {
        if (sum == target) {
            // we've reached one combination!
            result.push_back(combination);
            return;
        }

        if (sum > target || i >= candidates.size()) {
            // sum exceeded or i went OOB
            // tree does not grow anymore
            return;
        }

        // decision to include candidates[i]
        combination.push_back(candidates[i]);
        // notice we are starting from i again, because we are allowed to use a number more than once
        dfs(candidates, target, i, sum + candidates[i], combination, result); 

        // decision NOT to include candidates[i] at all
        combination.pop_back();
        // starting from i+1, sum not modified
        dfs(candidates, target, i+1, sum, combination, result);

    }
};

---

💡 Permutations

Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order.

Example 1:

Input: nums = [1,2,3]
Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

Example 2:

Input: nums = [0,1]
Output: [[0,1],[1,0]]

Example 3:

Input: nums = [1]
Output: [[1]]

Solution

class Solution {
public:
    vector<vector<int> > permute(vector<int> &num) {
	    vector<vector<int> > result;
	    
	    permuteRecursive(num, 0, result);
	    return result;
    }
    
    // permute num[begin..end]
    // invariant: num[0..begin-1] have been fixed/permuted
	void permuteRecursive(vector<int> &num, int begin, vector<vector<int> > &result)	{
		if (begin >= num.size()) {
		    // one permutation instance
		    result.push_back(num);
		    return;
		}
		
		for (int i = begin; i < num.size(); i++) {
		    swap(num[begin], num[i]);
		    permuteRecursive(num, begin + 1, result);
		    // reset
		    swap(num[begin], num[i]);
		}
    }
};