🙋🏻 Bottom-up

가장 작은 문제들 부터 답을 구해가며 전체 답을 찾는 방식

피보나치 함수 구현을 예로 들자면,,

int fibonacci(int n)
{
    dp[0] = 0, dp[1] = 1;
    // 작은 문제부터,,
    for (int i = 2; i <= n; i++)
        dp[i] = dp[i - 1] + dp[i - 2];
}

recursion이 아니라, 시간과 메모리 사용량을 줄일 수 있다

🙋🏻 Top-down

큰 문제를 방문 후 작은 문제를 호출하여 답을 찾는 방식

int fibonacci(int n)
{
    if (n == 0) return 0;
    if (n == 1) return 1;
 
    if (dp[n] != -1) return dp[n];
 	
    // 큰문제 방문해서 거기서 recursion으로 작은 문제를 호출! 
    dp[n] = fibonacci(n - 1) + fibonacci(n - 2);
    return dp[n];
}

점화식을 이해하기 쉽다

---

💡 Climbing Stairs

You are climbing a staircase. It takes n steps to reach the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Example 1:

Input: n = 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps

Example 2:

Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

Solution

근데 왜 이전 두개를 더하는거야,, 이해가 안돼 나 바본가

아 ! !!

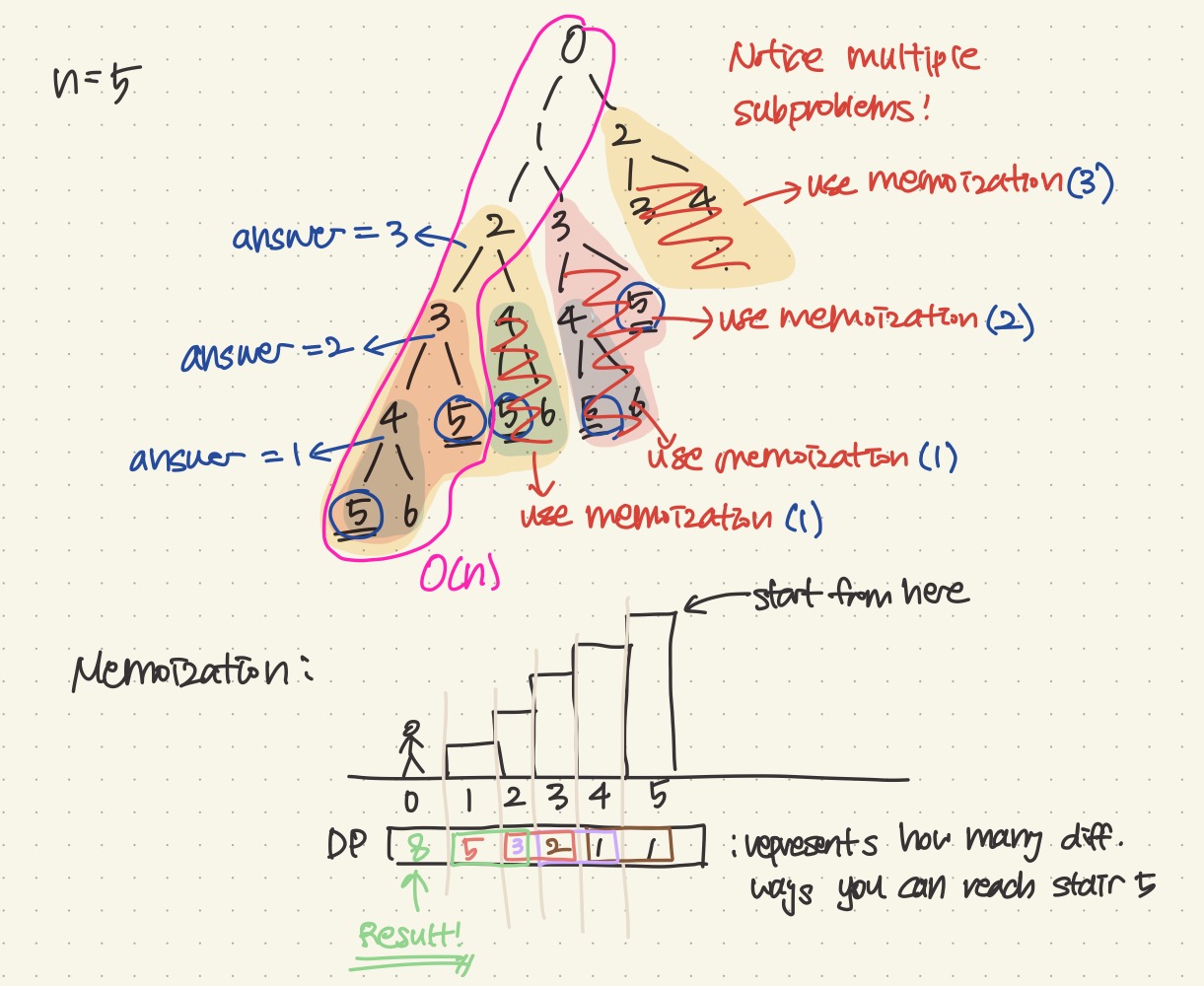
그니까 내가 지금 stair 2에 있다고 치자
그럼 내가 갈 수 있는 곳은 stair 3과 4이다 (한번에 1 step or 2 step만 갈 수 있으니)
그러므로 stair 3이나 4에서 5로 갈 수 있는 경우의 수를 더해주면
내가 stair 2에서 5로 갈 수 있는 경우의 수가 계산 되는 것이다!

(notice: 마지막 두개는 항상 1로 채워지고 시작한다)
생각해보자

stair 4 (마지막 두번째)에서 stair 5로 (마지막) 가는 방법은 하나니까 당연히 1
stair 5는 다른 더 밑에 단계 계단에서 1계단 올라가는 것을 미리 고려해서 적어준것!

Bottom up

class Solution {
public:
    int climbStairs(int n) {
        int one_step = 1;
        int two_step = 1;

        for (int i = 0; i <= n - 2; i++) { // 마지막 두 계단은 1로 이미 계산 되어있으니, 
                                           //  그 마지막 두 계단 전까지만 loop을 돌면 된다
            int temp = one_step;
            one_step = one_step + two_step;
            two_step = temp;
        }

        return one_step;
    }
};

Top down

... 모르겟삼

---

💡 Min Cost Climing Stairs

You are given an integer array cost where cost[i] is the cost of ith step on a staircase. Once you pay the cost, you can either climb one or two steps.

You can either start from the step with index 0, or the step with index 1.

Return the minimum cost to reach the top of the floor.

Example 1:

Input: cost = [10,15,20]
Output: 15
Explanation: You will start at index 1.
- Pay 15 and climb two steps to reach the top.
The total cost is 15.

Example 2:

Input: cost = [1,100,1,1,1,100,1,1,100,1]
Output: 6
Explanation: You will start at index 0.
- Pay 1 and climb two steps to reach index 2.
- Pay 1 and climb two steps to reach index 4.
- Pay 1 and climb two steps to reach index 6.
- Pay 1 and climb one step to reach index 7.
- Pay 1 and climb two steps to reach index 9.
- Pay 1 and climb one step to reach the top.
The total cost is 6.

Solution

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int two = cost[0]; // min cost when taking the 2 stairs before
        int one = cost[1]; // min cost when taking the 1 stair before

        int curr = INT_MAX; // cost of the current stair, indeed the result

        for (int i = 2; i <= cost.size(); i++) {
            int c = 0;
            if (i != cost.size()) c = cost[i];

            curr = min(two + c, one + c);

            // update two, one for the next stari
            two = one;
            one = curr;
        }

        return curr;
    }
};

---

💡 Longest Palindromic Substring

Given a string s, return the longest palindromic substring in s.

Example 1:

Input: s = "babad"
Output: "bab"
Explanation: "aba" is also a valid answer.

Example 2:

Input: s = "cbbd"
Output: "bb"

Solution

일단 아까 지하철에서 봤던 영상이라 복기를 해보면서 혼자 풀어보자

아이디어는:
each letter가 palindrome의 가운데라고 생각한 상태로 계속 양쪽으로 퍼져나가는 것이다
하지만, palindrome이 짝수일수도 있을테니, 그럴 경우를 생각해 i, i+1 를 묶어서 가운데라고 생각하여 퍼져나가는 방법도 consider 해주어야한다

class Solution {
public:
    string longestPalindrome(string s) {
        int result_start = 0;
        int result_length = 0;

        for (int i = 0; i < s.size(); i++) {
            palindrome(s, i, i, result_start, result_length);
            palindrome(s, i, i+1, result_start, result_length);
        }

        return s.substr(result_start, result_length);
        
    }

private:
    void palindrome(string s, int i, int j, int &result_start, int &result_length) {
        while (i >= 0 && j < s.size()) {
            if (s[i] != s[j]) break;

            if (result_length < j - i + 1) {
                result_start = i;
                result_length = j - i + 1;
            }
            
            i--;
            j++;
        }
    }
};

---

💡 Palindromic Substrings

Given a string s, return the number of palindromic substrings in it.

A string is a palindrome when it reads the same backward as forward.

A substring is a contiguous sequence of characters within the string.

Example 1:

Input: s = "abc"
Output: 3
Explanation: Three palindromic strings: "a", "b", "c".

Example 2:

Input: s = "aaa"
Output: 6
Explanation: Six palindromic strings: "a", "a", "a", "aa", "aa", "aaa".

Solution

위의 문제랑 거의 비슷하다! 이제 모든 경우의 수를 세어주기만 하면 된다

class Solution {
public:
    int countSubstrings(string s) {
        int result = 0;

        for (int i = 0; i < s.size(); i++) {
            palindrome(s, i, i, result);
            palindrome(s, i, i+1, result);
        }

        return result;
        
    }

private:
    void palindrome(string s, int i, int j, int &result) {
        while (i >= 0 && j < s.size()) {
            if (s[i] != s[j]) break;

            result++;
            
            i--;
            j++;
        }
    }
};

---

💡 Longest Increasing Subsequence

Given an integer array nums, return the length of the longest strictly increasing subsequence

Example 1:

Input: nums = [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.

Example 2:

Input: nums = [0,1,0,3,2,3]
Output: 4

Example 3:

Input: nums = [7,7,7,7,7,7,7]
Output: 1

Solution

Subsequence를 구하는 문제라서, 어떤 element를 사용할지 처음부터 계속 체크하여 업데이트 해주어야 한다

이런식으로...

for (int i = 0; i < n; i++) {
	for (int j = 0; j < i; j++) {
    //...
    }
}

(Note: Subarray를 구하는 문제에서는 조건에 어긋나면 현재 element부터 다시 시작했었다!)

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n, 1);
        
        int result = 1;

        for (int i = 1; i < n; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[j] < nums[i]) {
                    // nums[j]를 포함하는 subsequence가 더 길다면 update 해준다
                    //  nums[i] 이전의 dp값들은 모두 최신(= the final longest subsequence) 값을 가지고 있다
                    dp[i] = max(dp[i], dp[j] + 1);
                    
                }
            }
            result = max(result, dp[i]);
        }
        
        return result;
    }
};

---

💡 Maximum Subarray

Given an integer array nums, find the subarray which has the largest sum and return its sum.

Example 1:

Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

Example 2:

Input: nums = [1]
Output: 1

Example 3:

Input: nums = [5,4,-1,7,8]
Output: 23

Solution

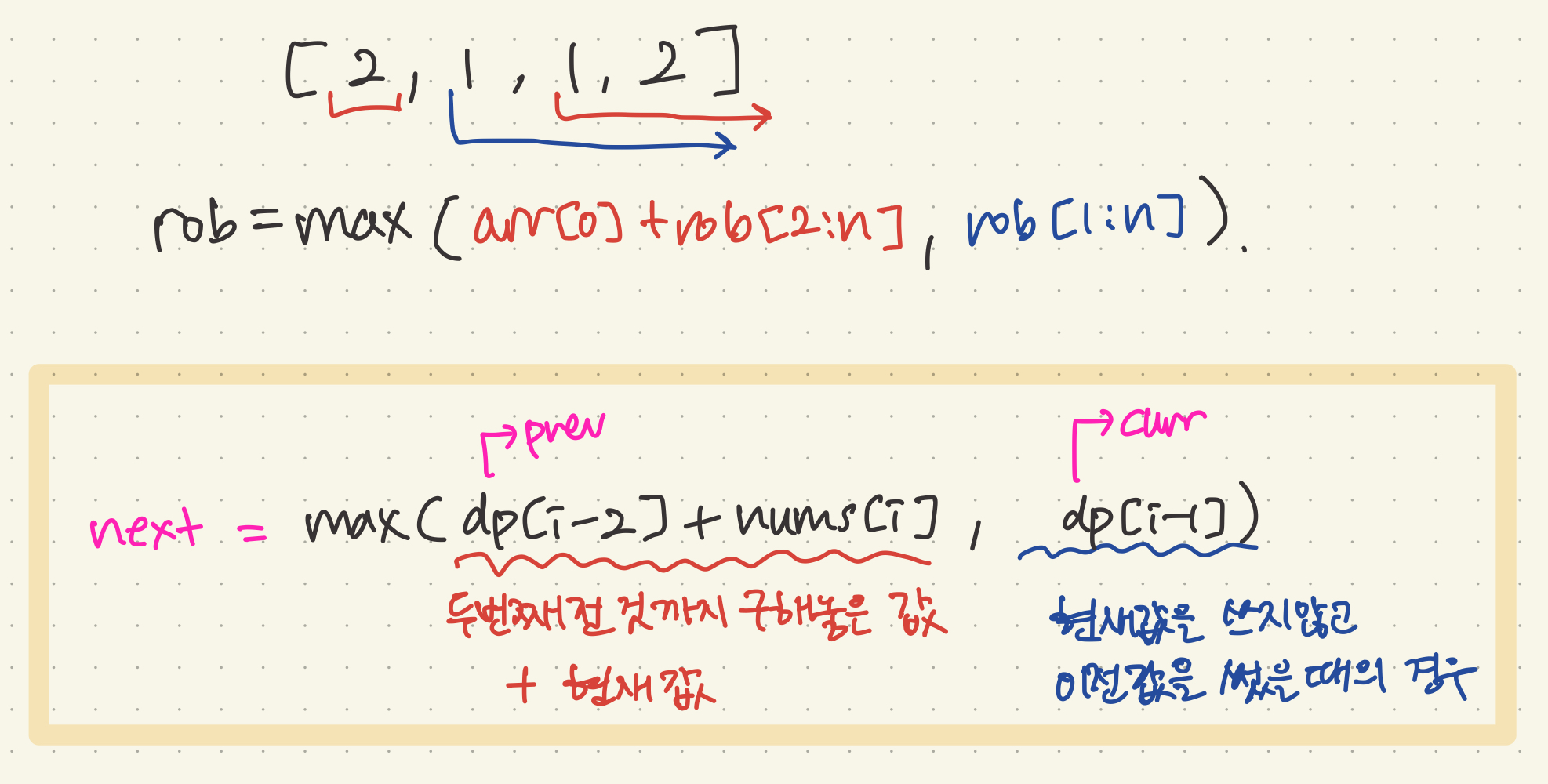
nums[0:i+1]의 maximum subarray는 이 둘 중 하나이다

1. 현재 요소(i)의 값 이거나
2. 이전에 구했던 부분집합의 최대 값 + 현재 요소

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int result = INT_MIN;
        int cur_sum = 0;

        for (int i = 0; i < nums.size(); i++) {
            // cur_sum은 지금까지 max sum을 가지고있는 subarray의 sum을 보관
            //  그래서 지금 여기서 뭘 하는거냐면
            //  subarray를 초기화 하고 여기부터 다시 시작할때가 크냐 (nums[i])
            //  아니면 subarray로 계속 이어서 현재 값을 포함했을때가 더 크냐 (nums[i] + cur_sum)
            cur_sum = max(nums[i], nums[i] + cur_sum);
            result = max(cur_sum, result);
        }

        return result;
    }
};

cur_sum 을 계속 max로 keep up 하는데 왜 final answer이 아니냐,,,면
cur_sum은 subarray의 시작위치가 여러가지로 고려되면서 가장 최근(not max) 시작위치에서부터의 max를 following 하기 때문에 result와 계속 비교해주면서 update해주어야 한다

---

💡 Maximum Product Subarray

product가 가장 큰 subarray를 찾는 문제이다
subarray는 continuous한 element로만 이룰 수 있다

.
.

이전 문제와 되게 유사해 보이지만 생각해야할게 하나 더 있다 (중요_

음수가 하나만 있으면 좋지만, 두개 (혹은 짝수개)가 있다면 maximum product에 영향을 준다.
우리는 어떻게 음수를 포기할지 아니면 가져갈지 결정해야할까?

→ track currMax & currMin

만약 현재 숫자가 음수라면, currMin에 곱해주면 maximum product를 가져다줄수도 있는것!
현재 숫자가 양수라면, currMax에 곱해주면 max product를 주겟징.
굳이 if로 양수 음수를 체크하지 않아도 이렇게 사용할 수 있다
max(currMax * nums[i], currMin * nums[i])

이제 이렇게 곱해준 값과와 현재 숫자를 비교 했을 때 더 큰수를 currMax에 저장하여 subarray를 재시작할건지, 이어갈건지 정하는거다

동시에 currMin도 update해주어야 한다
위의 로직과 비슷하게,
min(currMin * nums[i], currMax * nums[i]) 로 표현한다
단, currMax를 앞전에서 update해주었기 때문에, temp에 보관했어야 한다
마찬가지로 이 값과 현재값을 비교했을 때 더 작은 수를 currMin에 저장한다

Solution

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int currMax = nums[0];
        int currMin = nums[0];
        int result = nums[0];

        for (int i = 1; i < nums.size(); i++) {
            int temp = currMax;
            currMax = max(max(currMax * nums[i], currMin * nums[i]), nums[i]);
            currMin = min(min(temp * nums[i], currMin * nums[i]), nums[i]);

            result = max(result, currMax);
        }

        return result;               
    }
};

---

💡 Unique Paths

There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.

The test cases are generated so that the answer will be less than or equal to 2 * 10^9.

Example 1:

Input: m = 3, n = 7
Output: 28

Example 2:

Input: m = 3, n = 2
Output: 3
Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down

Solution

각각의 cell에서 그곳까지의 unique path를 계산 해서 보관하면 되겟당

지금 cell에서 unique path를 계산 하는 방법은
로봇이 down or right만 움직일 수 있다고 했으니간 ..
위에서 왔거나 왼쪽에서 왔을거니깐,,

• cell[i-1][i] (위) + cell[i][i-1] (왼쪽) 하면 되겟당

그리구 ,, cell은 모두 0으로 initialize 해야하고
(except for the base cases)

• base case는 start robot의 아래, 오른쪽 cell이다
  1로 initialize 하면 되겟군 ,,
  .
  .
  이 아니라 base case는
  오른쪽 쭉~ 한줄, 아래 쭉~ 한줄을 다 1로 초기화 해줘야겠다.
  이렇게 해주지않으면 for loop을 index 1에서 시작하므로
  1st row, 1st column은 방문이 안되기 때문에 0으로 기록되어있어서 틀린 답을 뱉어낸다

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> grid(m, vector<int>(n)); // initialized with 0

        // basecase
        // the row and column that contains the start cell
        for (int i = 0; i < m; i++) {
            grid[i][0] = 1;
        }
        for (int j = 0; j < n; j++) {
            grid[0][j] = 1;
        }
        
        // now dp!
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                grid[i][j] = grid[i-1][j] + grid[i][j-1];
            }
        }

        return grid[m-1][n-1];
    }
};

---

💡 Unique Path II

You are given an m x n integer array grid. There is a robot initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

An obstacle and space are marked as 1 or 0 respectively in grid. A path that the robot takes cannot include any square that is an obstacle.

Return the number of possible unique paths that the robot can take to reach the bottom-right corner.

Example 1:

Input: obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
Output: 2
Explanation: There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right

Example 2:

Input: obstacleGrid = [[0,1],[0,0]]
Output: 1

Solution

위의 solution에서 obstacle에 관한 condition들만 조금 더 추가해주었다.
주어진 obstacleGrid를 dp로 덮어씌워 계산하는게 특징이다

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        if (obstacleGrid[0][0] == 1)
            return 0;
        
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();

        // reuse the obstacleGrid as the dp calculation matrix

        obstacleGrid[0][0] = 1; //the start point initialized as 1

        // the first row
        for (int i = 1; i < m; i++) {
            // if the current cell has the obstacle (has 1 in the cell)
            // or the previous cell had 0 path to the cell 
            //    (means there was a obstacle during this straight path journey)
            if (obstacleGrid[i][0] == 1 || obstacleGrid[i-1][0] == 0)
                obstacleGrid[i][0] = 0;
            else 
                obstacleGrid[i][0] = 1;
        }

        // the first column
        for (int j = 1; j < n; j++) {
            // 여기도 위에랑 똑같이
            // 현재 cell에 장애물이 있거나 혹은
            // 이전 cell이 0으로 mark되어있다면 장애물이 전에 어딘가에 있던단 뜻
            if (obstacleGrid[0][j] == 1 || obstacleGrid[0][j-1] == 0)
                obstacleGrid[0][j] = 0;
            else
                obstacleGrid[0][j] = 1;
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (obstacleGrid[i][j] == 1) { 
                    obstacleGrid[i][j] = 0;
                } else {
                    obstacleGrid[i][j] = obstacleGrid[i-1][j] + obstacleGrid[i][j-1];
                }
            }
        }

        return obstacleGrid[m-1][n-1];

    }
};

---

💡 House Robber

You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security systems connected and it will automatically contact the police if two adjacent houses were broken into on the same night.

Given an integer array nums representing the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police.

Example 1:

Input: nums = [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.

Example 2:

Input: nums = [2,7,9,3,1]
Output: 12
Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
Total amount you can rob = 2 + 9 + 1 = 12.

Solution

class Solution {
public:
    int rob(vector<int>& nums) {
        int prev = 0;
        int curr = 0;
        int next = 0;

        for (int i = 0; i < nums.size(); i++) {
            next = max(prev + nums[i], curr);
            prev = curr;
            curr = next;
        }

        return curr;
    }
};

---

💡 House Robber II

same as the previous question, except for that the house is are placed in a circle

Solution

집이 동그랗게 이어져 있으므로 마지막집을 rob한다면 첫번째 집을 rob해서는 안된다

class Solution {
public:
    int rob(vector<int>& nums) {
        int n = nums.size();
        if (n == 1) return nums[0];
		
        // 만약 첫번재 집을 rob한다면 맨 마지막 집은 후보에서 제외
        int from_0 = robber(nums, 0, n - 1);
        // 첫번째 집을 rob하지 않는다면 마지막집도 rob할 가능성 열어둠
        int from_1 = robber(nums, 1, n);

        return max(from_0, from_1);
    }
private:
    int robber(vector<int>& nums, int start, int end) {
        int prev = 0; // 2before    
        int curr = 0; // 1before
        int next = 0; // current

        for (int i = start; i < end; i++) {
            next = max(prev + nums[i], curr);
            prev = curr;
            curr = next;
        }

        return curr;
    }
};

---

💡 Best Time to Buy and Sell Stock

You are given an integer array prices where prices[i] is the price of a given stock on the ith day.

On each day, you may decide to buy and/or sell the stock. You can only hold at most one share of the stock at any time. However, you can buy it then immediately sell it on the same day.

Find and return the maximum profit you can achieve.

Example 1:

Input: prices = [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
Total profit is 4 + 3 = 7.

Example 2:

Input: prices = [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Total profit is 4.

Example 3:

Input: prices = [7,6,4,3,1]
Output: 0
Explanation: There is no way to make a positive profit, so we never buy the stock to achieve the maximum profit of 0.

Solution

생각해보면 계속 값이 오른다고 볼 때

• 3번째에 사서 6번째에 판매하는 값 (6번째 - 3번째)
• 3번째에 사서 4번째에서 팔고, 다시 4번째에서 사서 5번째에서 팔고, 다시 5번째에서 사서 6번째에서 판 값 (6번째 - 5번쨰 + 5번째 - 4번째 + 4번쨰 - 3번째)

이 두값이 결국 같은 profit이다
판곳에서 바로 다시 살 수 있다는 조건이 있기 때문에 가능 한 일이다

또 값이 내려간다면 팔지 않을 것이니까 올라갈때 까지 대기탄다
계속 내려가다가 값이 올라간다면 계속 내려간 마지막 값이 제일 작은 값이므로 거기서 사서 다음날 팔면 그게 max profit이다

그러므로 하루 차이로 주식을 사고팔고를 반복해서 positive number면 profit에 계속 더해주면 된다

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int profit = 0;
        int n = prices.size();

        for (int i = 1; i < n; i++) {
            profit += max(0, prices[i] - prices[i-1]);
        }

        return profit;
    }
};

---

💡 Best Time to Buy and Sell Stock with Cooldown

You are given an array prices where prices[i] is the price of a given stock on the ith day.

Find the maximum profit you can achieve. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times) with the following restrictions:

• After you sell your stock, you cannot buy stock on the next day (i.e., cooldown one day).

Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).

Example 1:

Input: prices = [1,2,3,0,2]
Output: 3
Explanation: transactions = [buy, sell, cooldown, buy, sell]

Example 2:

Input: prices = [1]
Output: 0

Solution

Consider the different profits if we buy, sell, or cooldown on Day i.

Use 3 variables to track max profits if our last action is to buy, sell, or cooldown TILL Day i.

Be careful about what action we took TILL Day i-1,
if we choose to do certain actions ON Day i.

• Buy today
  → the last action till yesterday MUST BE cooldown
  compare: cooldown yesterday and buy today vs. max profit yesterday when the last action is to buy (keeping 'buy' status)

• Sell today
  → the last action till yesterday MUST BE buy
  compare: sell the stock based on the last buy vs. max profit yesterday when the last action is to sell (keeping 'sell' status)

• Cooldown today
  → the last action till yesterday MUST BE sell OR cooldown
  compare: max profit yesterday when the last actioin is sell vs. max profit yesterday when the last action is cooldown

We always need to check if we decide to buy/sell/cooldown today, can we earn more profit than yesterday, if not, we will give up and remain the max profit we met so far.

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.size() <= 1) return 0;

        // max profit value for each of the actions from yesterday
        int cooled = 0;
        int sold = 0;
        int bought = 0;

        //on the first day, the only choice is to buy
        bought -= prices[0];
        
        for (int i = 1; i < prices.size(); i++) {
            int cooled_temp = cooled;
            int sold_temp = sold;
            int bought_temp = bought;

            bought = max(cooled_temp - prices[i], bought_temp);
            sold = max(bought_temp + prices[i], sold_temp);
            cooled = max(sold_temp, cooled_temp);
        }

        return max(sold, cooled); //only can do sell or cooldown on the lastday
    }
};

---

💡 Word Break

Given a string s and a dictionary of strings wordDict, return true if s can be segmented into a space-separated sequence of one or more dictionary words.

Note that the same word in the dictionary may be reused multiple times in the segmentation.

Example 1:

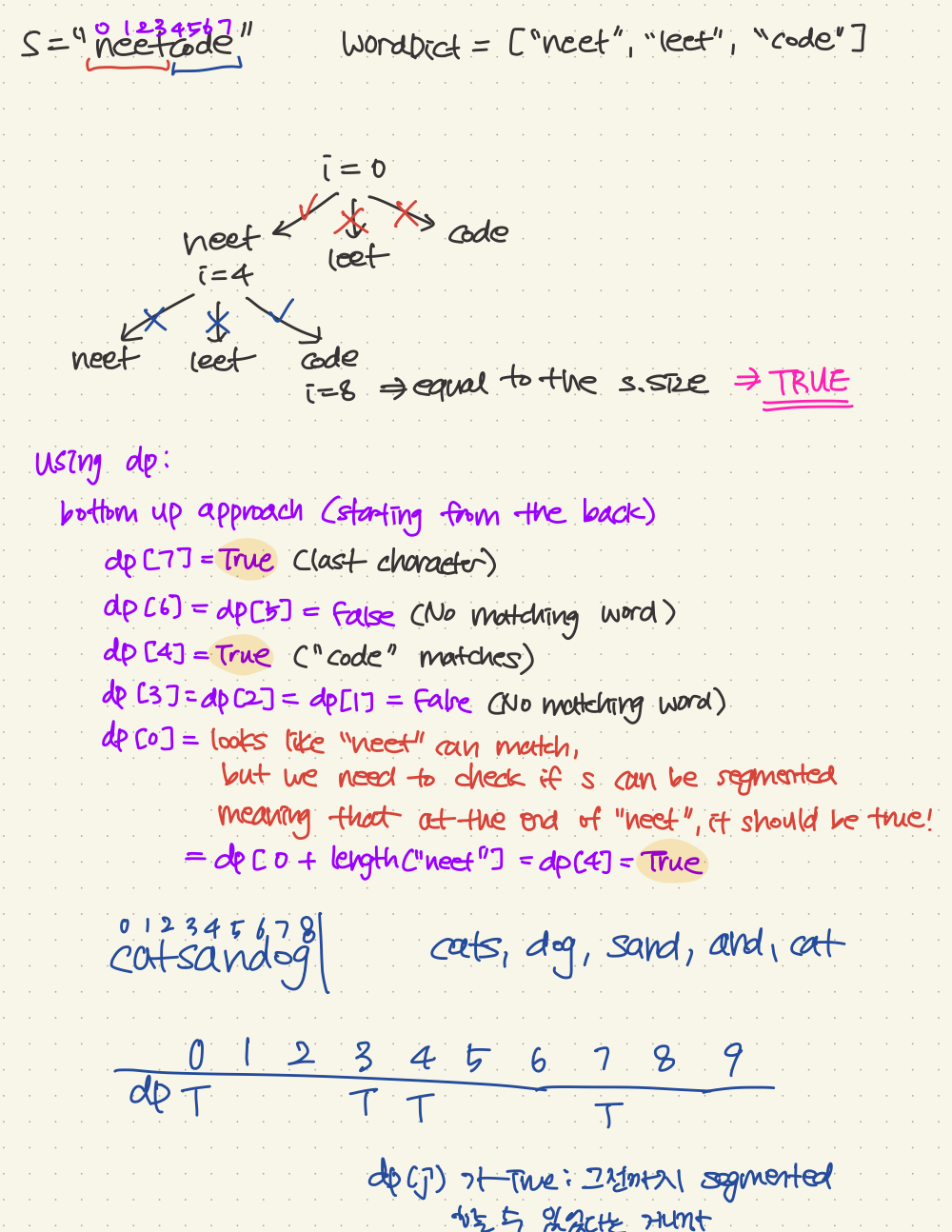
Input: s = "leetcode", wordDict = ["leet","code"]
Output: true
Explanation: Return true because "leetcode" can be segmented as "leet code".

Example 2:

Input: s = "applepenapple", wordDict = ["apple","pen"]
Output: true
Explanation: Return true because "applepenapple" can be segmented as "apple pen apple".
Note that you are allowed to reuse a dictionary word.

Example 3:

Input: s = "catsandog", wordDict = ["cats","dog","sand","and","cat"]
Output: false

Solution

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        // store the words from dictionary to hash for constant lookup
        unordered_set<string> word_dict;
        for (int i = 0; i < wordDict.size(); i++) {
            word_dict.insert(wordDict[i]);
        }

        int n = s.size();
        vector<bool> dp(n + 1);
        // dp에서 true를 기준으로 new substring을 시작하기 때문에 
        // 첫번째 letter에서 true로 지정해주어야 한다
        dp[0] = true;

        // let's process the string bottom up
        for (int i = 1; i <= n; i++) {
            for (int j = i-1; j >= 0; j--) {
                if (dp[j]) {
                    // dp[j] == true 이면 s[0:j]가 segmented 될 수 있다는 것이고,
                    //   s[0:j]에서 끊고,
                    //   s[j:]부터 matching을 시작해야 된다!
                    string substring = s.substr(j, i - j); //substr(starting index, length)
                    if (word_dict.find(substring) != word_dict.end()) {
                        // if this substring exists in the dictionary
                        dp[i] = true; // meaning that s[j:i+1] exists in the dict
                        break;
                    }
                }
            }
        }

        return dp[n];
    }
};

---

💡 Coin Change

You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.

Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

You may assume that you have an infinite number of each kind of coin.

Example 1:

Input: coins = [1,2,5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1

Example 2:

Input: coins = [2], amount = 3
Output: -1

Example 3:

Input: coins = [1], amount = 0
Output: 0

Solution

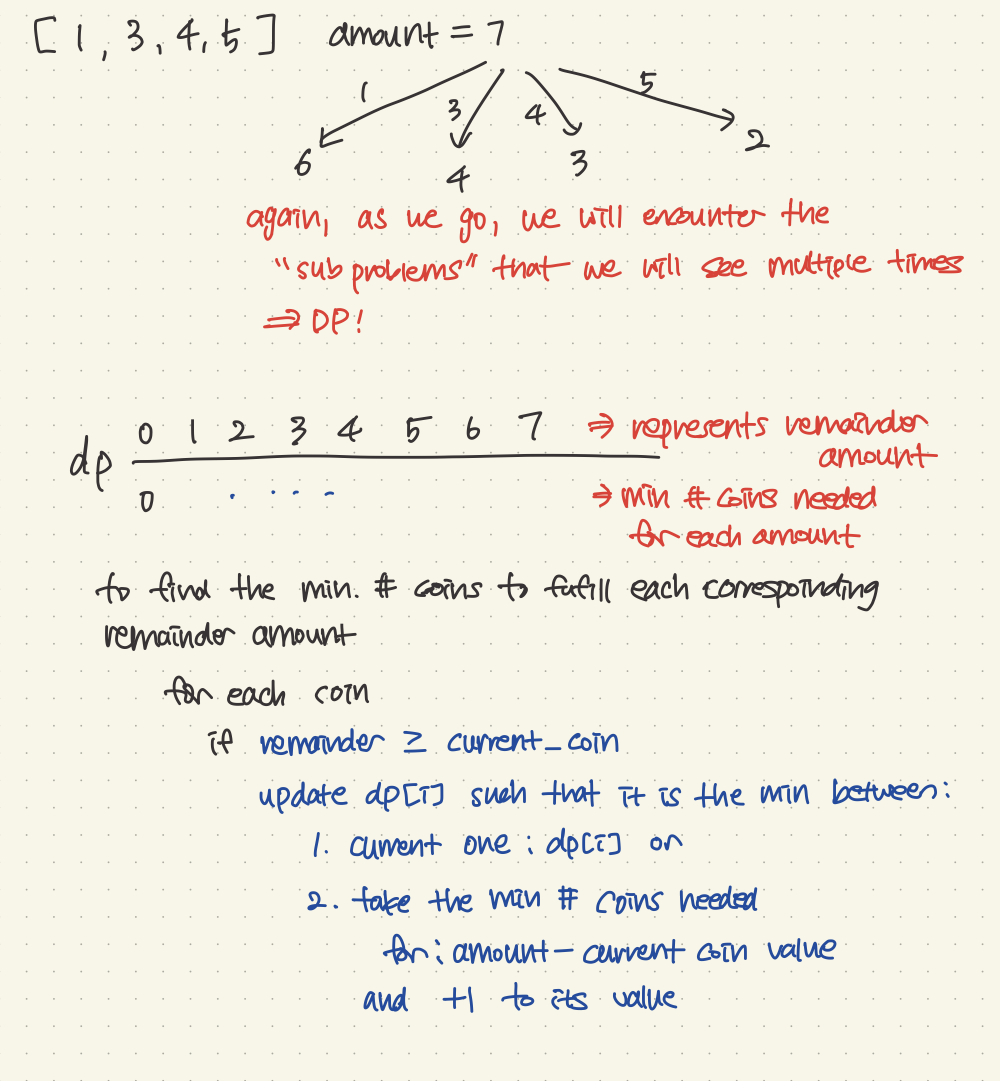
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        // each index in dp represents the remainder
        // dp[i] will represent minimum # of coins to fulfill the corresponding remainder amount
        vector<int> dp(amount + 1, amount + 1); // initialize #coins to max number
        										// cannot initialize with INT_MAX, 
                                                // because we perfrom + 1 operation when taking min

        // to fulfill 0 cost, we need 0 coins
        dp[0] = 0;

        for (int i = 1; i <= amount; i++) {
            for (int c = 0; c < coins.size(); c++) {
                if (i >= coins[c]) { //if this coin fits into remainder amount
                    // update current dp such that is the minimum between
                    //   the current dp
                    //    or
                    //   when using this coin
                    dp[i] = min(dp[i], dp[i - coins[c]] + 1);
                }
            }
        }

        if (dp[amount] == amount + 1) return -1;
        return dp[amount];


    }
};

---

💡 Coin Change II

You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.

Return the number of combinations that make up that amount. If that amount of money cannot be made up by any combination of the coins, return 0.

Example 1:

Input: amount = 5, coins = [1,2,5]
Output: 4
Explanation: there are four ways to make up the amount:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

Example 2:

Input: amount = 3, coins = [2]
Output: 0
Explanation: the amount of 3 cannot be made up just with coins of 2.

Solution

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        int n = coins.size();

        // sort coins vector
        sort(coins.begin(), coins.end());

        vector<vector<int>> dp(amount + 1, vector<int>(n));

        // initialize the basecase
        for (int j = 0; j < n; j++) {
            dp[0][j] = 1;
        }

        for (int i = 1; i <= amount; i++) {
            for (int j = n - 1; j >= 0; j--) {
                if (coins[j] > i) {
                    dp[i][j] = 0;
                } else {
                    dp[i][j] += dp[i - coins[j]][j]; // comb. using this coin
                    if (j != n - 1) 
                        dp[i][j] += dp[i][j+1]; // ALL the other comb. w/o using this coin
                }
            }
        }

        return dp[amount][0];

    }
};

---

💡 Decode Ways

Given a string w/ only digits, return # ways to decode it (letter → digit)

s = "12" -> 2 (AB 1 2 or L 12)
s = "226" -> 3 (2 26 or 22 6 or 2 2 6)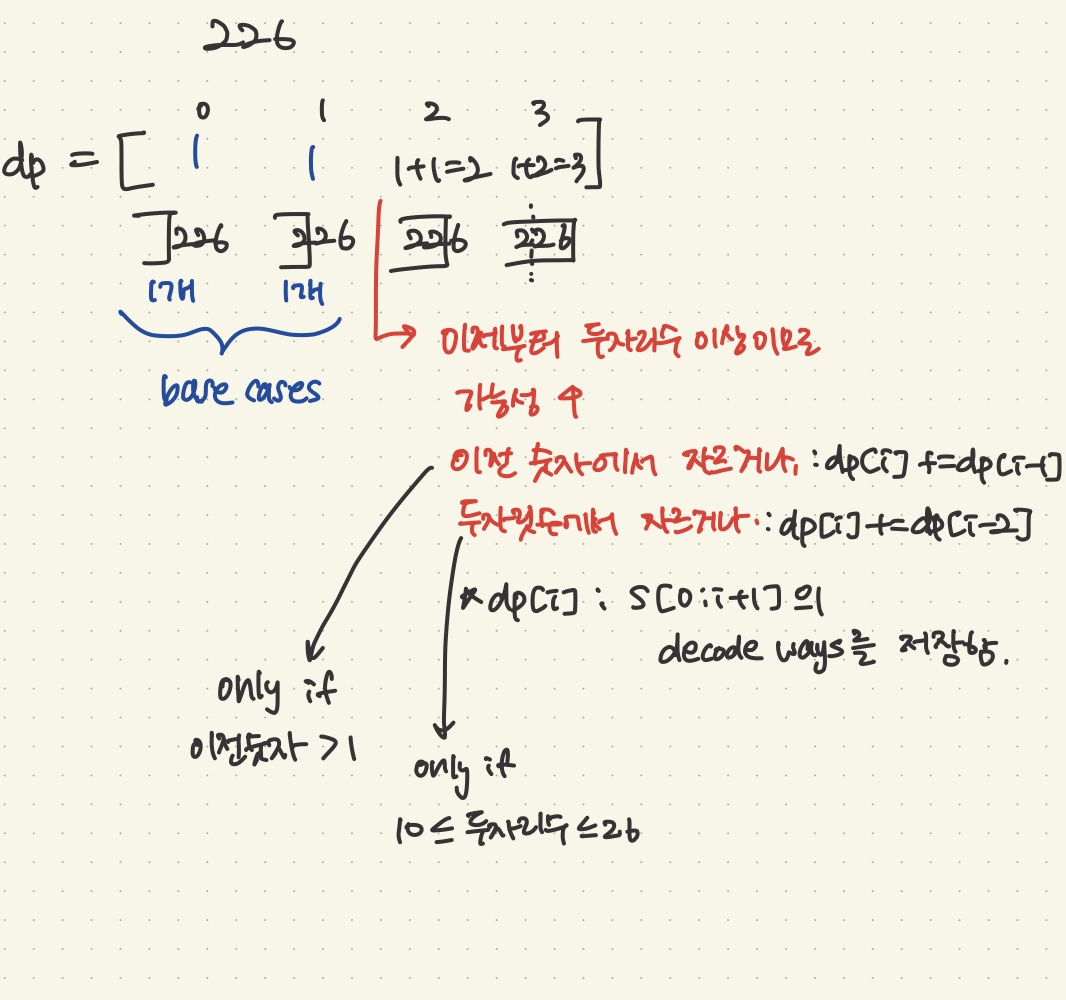

class Solution {
public:
    int numDecodings(string s) {
        if (s[0] == '0') {
            return 0;
        }
        
        int n = s.size();
        
        vector<int> dp(n + 1);
        dp[0] = 1;
        dp[1] = 1;
        
        for (int i = 2; i <= n; i++) {
            int ones = stoi(s.substr(i - 1, 1));
            if (ones > 0) {
                dp[i] += dp[i - 1];
            }
            int tens = stoi(s.substr(i - 2, 2));
            if (tens >= 10 && tens <= 26) {
                dp[i] += dp[i - 2];
            }
        }
        
        return dp[n];
    }
};

---

💡 Partition Equal Subset Sum

Given a non-empty array nums containing only positive integers, find if the array can be partitioned into two subsets such that the sum of elements in both subsets is equal.

Example 1:

Input: nums = [1,5,11,5]
Output: true
Explanation: The array can be partitioned as [1, 5, 5] and [11].

Example 2:

Input: nums = [1,2,3,5]
Output: false
Explanation: The array cannot be partitioned into equal sum subsets.

Solution

일단 nums가 2개의 같은 합을 가진 subset으로 나눠질 수 있는지 확인이 필요하다
→ 모든 숫자를 다 더했을 때(=sum) 일단 짝수라면 가능성은 있는것
(홀수라면 바로 return false, 두개로 나눠질 수 없다)

이제 구한 sum을 이등분한 값을 target으로 정해두고,
nums의 숫자들로 만들 수 있는 모든 가능한 subset의 각각의 sum을 구한다
이중에 target이 있다면 true, 아니라면 false를 return한다

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int target = 0;
        for (int i = 0; i < nums.size(); i++) {
            target += nums[i];
        }

        if (target % 2 == 1) 
            return false;
        
        target /= 2;

        // now find each and every subset's sum
        // and store into hashset
        unordered_set<int> subset_sums;
        subset_sums.insert(0);

        for (int i = 0; i < nums.size(); i++) {
            unordered_set<int> _subset_sums;
            
            for (auto it = subset_sums.begin(); it != subset_sums.end(); it++) {
                if (*it + nums[i] == target) {
                    // the target reached
                    return true;
                }
                // for each of the subset sums generated so far, 
                // we will add nums[i] to those subset sums 
                // to store the subset sums using nums[i]
                _subset_sums.insert(*it + nums[i]);
                _subset_sums.insert(*it); // since we are generating new _subset_sum
                                          // need to do this because of the for loop on subset_sum
            }
            subset_sums = _subset_sums;
        }

        // when here, target sum wasn't created in the subset sum
        return false;

    }
};

---

💡 Longest Common Subsequence

Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.

Example 1:

Input: text1 = "abcde", text2 = "ace" 
Output: 3  
Explanation: The longest common subsequence is "ace" and its length is 3.

Example 2:

Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.

Example 3:

Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.

Solution

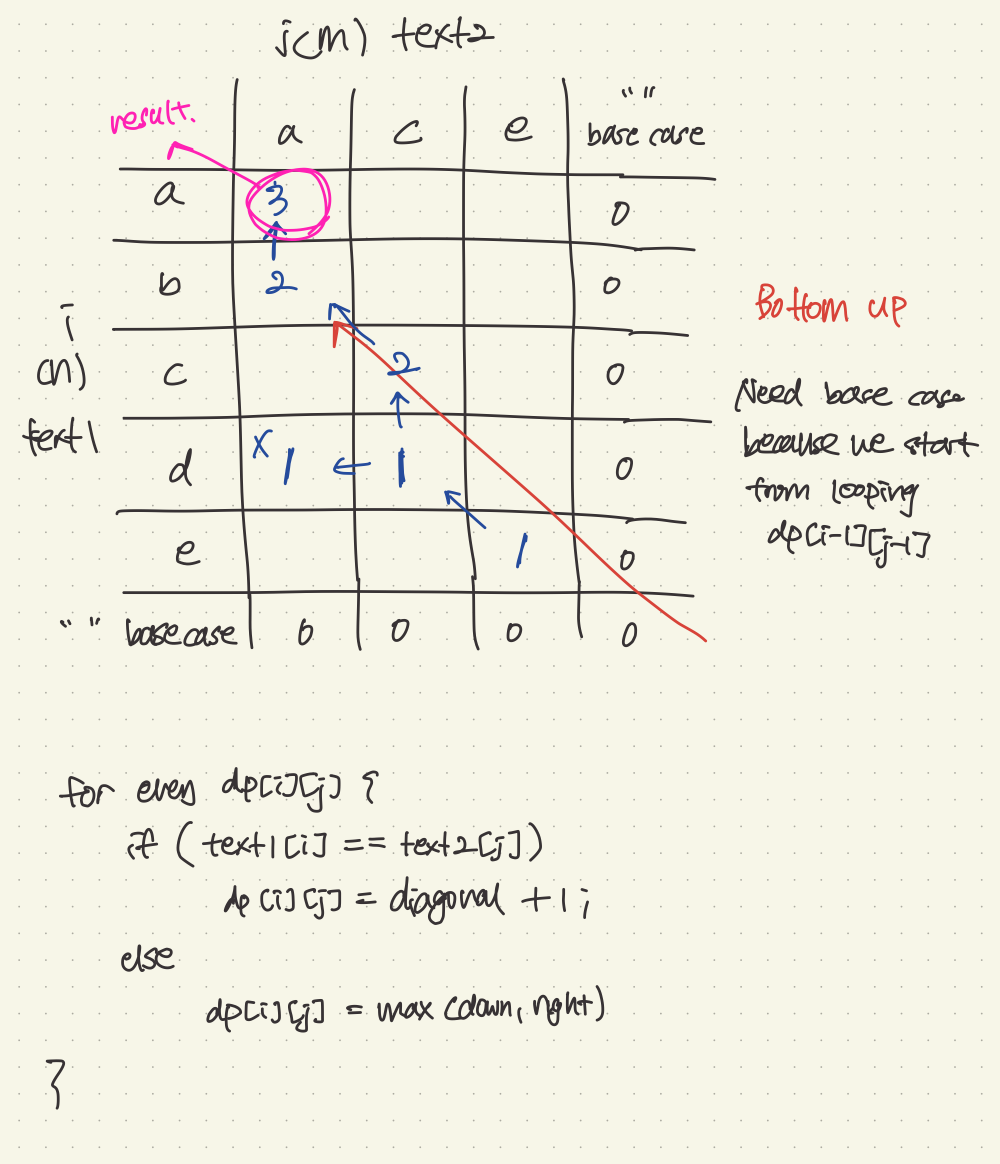
class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int n = text1.size();
        int m = text2.size();
        vector<vector<int>> dp(n+1, vector<int>(m+1)); //+1 for the basecase
        
        for (int i = n - 1; i >= 0; i--) {
            for (int j = m - 1; j >= 0; j--) {
                if (text1[i] == text2[j])
                    dp[i][j] = dp[i+1][j+1] + 1;
                else
                    dp[i][j] = max(dp[i+1][j], dp[i][j+1]);
            }
        }

        return dp[0][0];
    }
};

---

💡 Target Sum

You are given an integer array nums and an integer target.

You want to build an expression out of nums by adding one of the symbols '+' and '-' before each integer in nums and then concatenate all the integers.

For example, if nums = [2, 1], you can add a '+' before 2 and a '-' before 1 and concatenate them to build the expression "+2-1".
Return the number of different expressions that you can build, which evaluates to target.

Example 1:

Input: nums = [1,1,1,1,1], target = 3
Output: 5
Explanation: There are 5 ways to assign symbols to make the sum of nums be target 3.
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

Example 2:

Input: nums = [1], target = 1
Output: 1

Solution

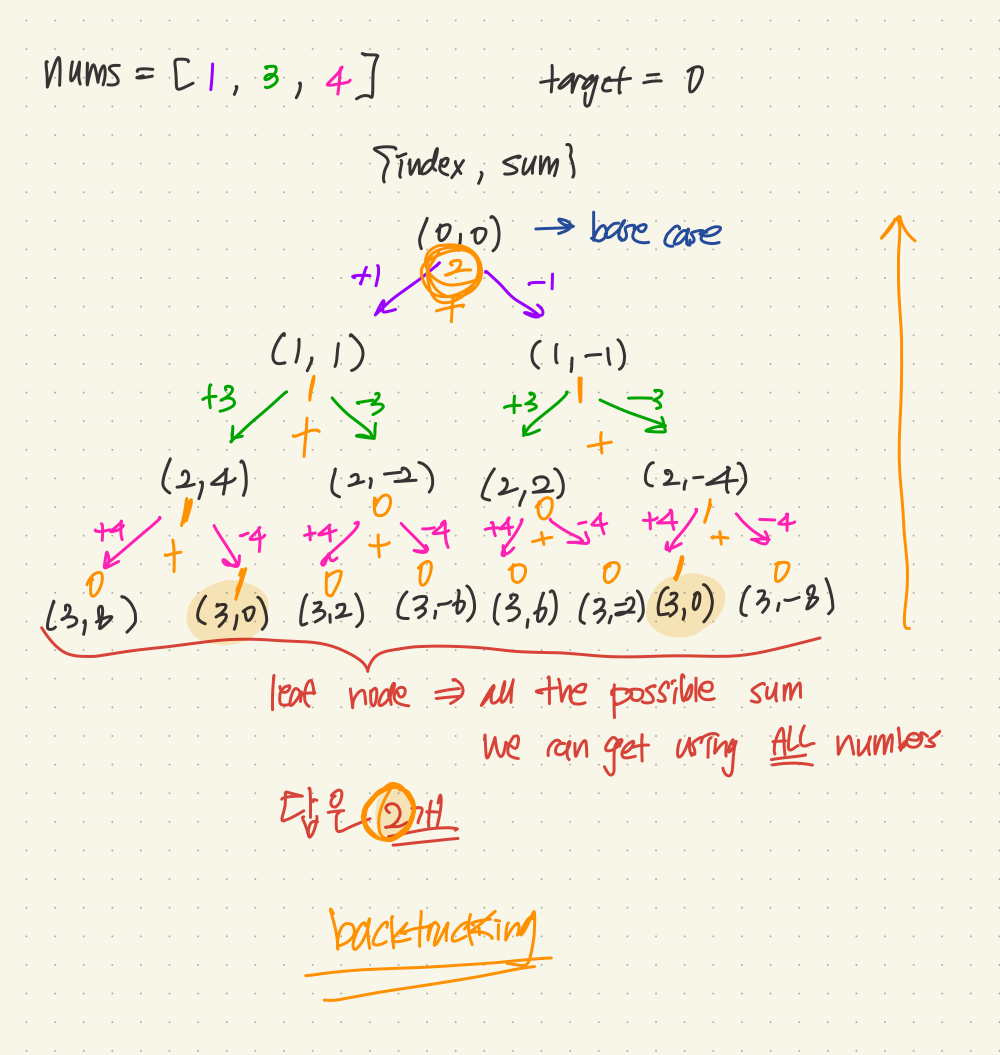
현재 숫자를 더하거나 빼거나 두가지 경우가 있다고 생각하고 코딩하면 간단하다

그렇게 숫자를 더하거나 뺐을 때 나오는 total을 같이 보관하자

{index, total} → # of ways
nums[index]를 포함 했을 때와 안포함 했을 때 이렇게 두가지로 map에는 같은 index를 가지고 있는 애들이 두개가 있게 된다.

base case:

• Valid: Index is out of bounds AND current sum is equal to target 'S'
• Invalid: Index is out of bounds

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        return backtrack(nums, target, 0, 0);
    }
private:
    // {(index, total) -> # of ways}
    map<pair<int, int>, int> dp;
    
    int backtrack(vector<int>& nums, int target, int i, int total) {
        if (dp.find({i, total}) != dp.end()) {
            // if the value was already calculted
            return dp[{i, total}];
        }

        // basecase when we used all the numbers
        if (i == nums.size()) {
            // Valid: current total is equal to target -> this is one valid expression! -> return 1
            // Invlid: current total is NOT equal to target
            return total == target ? 1 : 0;
        }
        
        // calculate the number of expressions if we add this number
        int positive = backtrack(nums, target, i + 1, total + nums[i]);
        // calculate the number of expressions if we subtract this number
        int negative = backtrack(nums, target, i + 1, total - nums[i]);

        // store the result to the map
        dp[{i, total}] = positive + negative;       
        
        return dp[{i, total}];
    }
};

---

💡 Longest Increasing Path

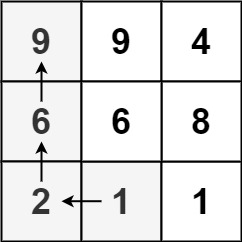
Solution

모든 cell들 돌면서 위, 아래, 오른쪽, 왼쪽에서부터 왔을 때 중에 longest increasing path를 불러와서
리턴한다.

dfs를 계속 돌지 않도록 cache (Dynamic Programming) 한다!

class Solution {
public:
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        
        int result = 0;
        
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                result = max(result, dfs(matrix, -1, i, j, m, n));
            }
        }
        
        return result;
    }
private:
    // {(i, j) -> longest increasing path at (i, j)}
    map<pair<int, int>, int> dp;
    
    int dfs(vector<vector<int>>& matrix, int prev, int i, int j, int m, int n) {
        // prev -> stores the value from where it came from
        if (i < 0 || i >= m || j < 0 || j >= n || matrix[i][j] <= prev) {
            // out of bound or 
            // current value is less than where it came from (we are looking for increasing path)
            return 0;
        }

        if (dp.find({i, j}) != dp.end()) {
            // if already performed use it 
            return dp[{i, j}];
        }
        
        // current cell count as 1
        int result = 1;
        // for every direction find the maximum path 
        result = max(result, 1 + dfs(matrix, matrix[i][j], i - 1, j, m, n));
        result = max(result, 1 + dfs(matrix, matrix[i][j], i + 1, j, m, n));
        result = max(result, 1 + dfs(matrix, matrix[i][j], i, j - 1, m, n));
        result = max(result, 1 + dfs(matrix, matrix[i][j], i, j + 1, m, n));
        dp[{i, j}] = result;
        
        return dp[{i, j}];
    }
};