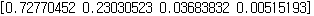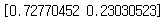1. PCA(주 성분 분석) 이란?
PCA는 차원축소(dimensionality reduction)와 변수추출(feature extraction) 기법으로 널리 쓰이고 있다.
주성분이란 전체 데이터(독립변수들)의 분산을 가장 잘 설명하는 성분을 말한다.
변수의 개수 = 차원의 개수
e.g.) iris 데이터에서, 4개의 독립변인들이 하나의 공간에 표현되기 위해서는, 공간이 4차원이어야 한다. → 차원이 증가할수록 데이터가 표현해야 하는 공간은 복잡해진다.
따라서, 변수가 너무 많아 기존 변수를 조합해 새로운 변수를 가지고 모델링을 하려고 할 때 주로 PCA를 사용한다. {이 때, 중요함의 기준은 전체 데이터(독립변수들, 모든 차원)의 변산을 얼마나 잘 설명하는가에 있다.}
2. PCA의 원리?
PCA 가 어떤 과정을 통해서 차원을 축소되는 것일까?
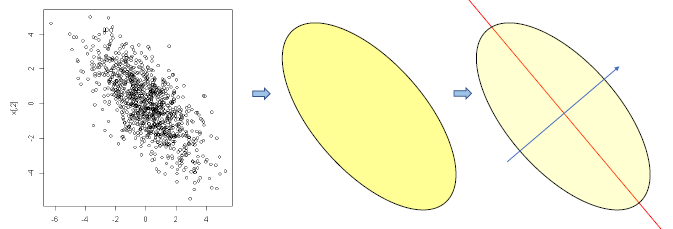
다음과 같은 2차원 데이터에 대해서 1차원으로 축소하는 것이 목적이라고 해보자.
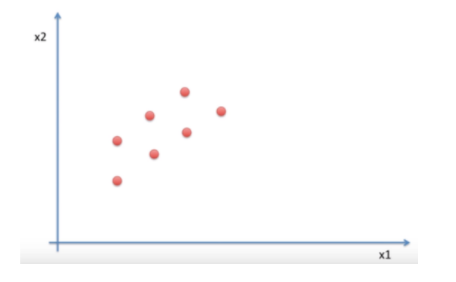
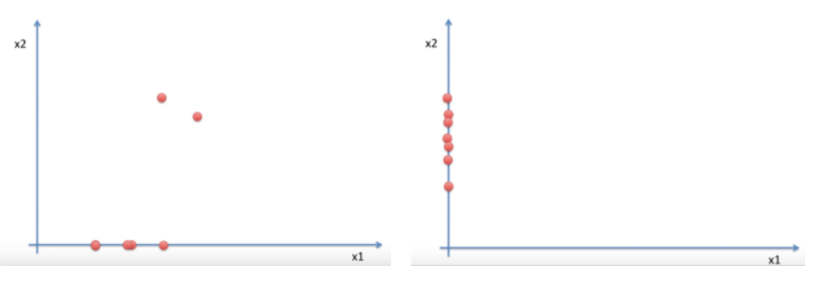
PCA 는 데이터를 1차원으로 축소하는 방법으로 정사영을 사용한다. 정사영을 하기 위한 축의 선택지는 다양하다. 아래 그림과 같이 x1 축으로 축소를 할 수 도 x2 축으로 축소를 할 수 도 있다.
하지만 기존 2차원일 때는 거리를 두고 있던 점들이 차원이 축소되며, 정사영 되면서 겹치게 되는 문제가 발생한다. 이 과정에서 기존의 정보가 유실된다고 볼 수 있다.
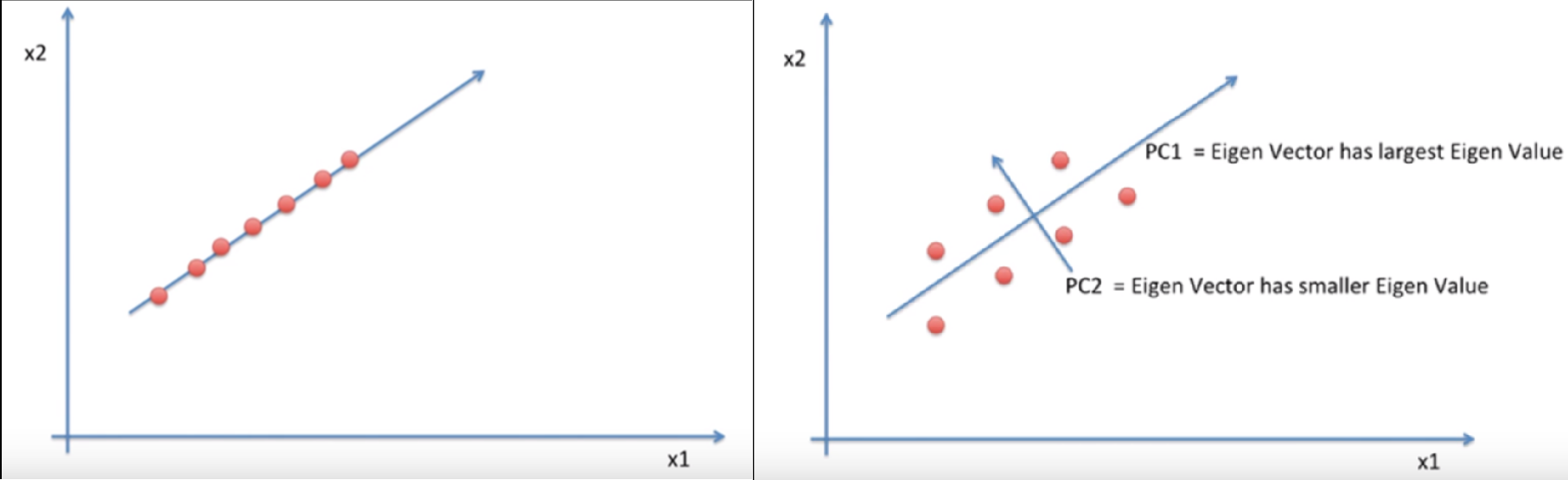
따라서 다음과 같이 x1, x2 축이 아닌 새로운 축을 찾아야 한다. 축은 각 점들이 퍼져있는 정도인 분산이 최대로 보존 될 수 있도록해야 한다. 그리고 이렇게 찾은 축을 principal component 줄여서 PC(주성분)이라고 한다.
PC를 찾기 위해서는 covaiance matrix(공분산 행렬) 의 eigen vector(고유 벡터) 값을 찾아야 하고, 이 값 중 가장 큰 값이 우리가 원하는 PC 에 만족한다고 볼 수 있으며 이를 PCA의 원리로 볼 수 있다.
3. PCA의 차원 축소(Feature Extraction), 분산을 최대로 보존할 수 있는 축을 선택하는 이유?
실제 데이터들의 대부분은 매우 많은 설명 변수(= 특성 = feature = 흔히 X 값)들을 가지고 있다. 따라서 머신러닝 알고리즘을 적용해서 문제를 해결하는 데 있어서 어려움이 있다.
이로 인헤, 전체 데이터의 양이 너무 많아서 학습 속도가 느려지거나 별로 의미없는 feature들로 인해서 과적합 또는 학습이 잘 되지 않는다.
그러므로 Feature selection(변수 추출)이나 Dimensionality Reduction(차원 축소) 등의 작업이 필요하다.
저차원의 초평면에 투영을 하게 되면 차원이 줄어들게 된다.
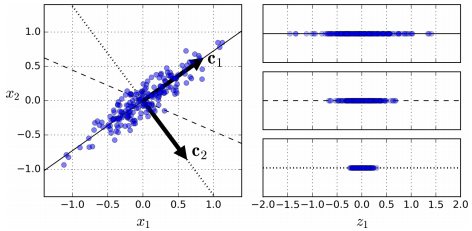
위와 같은 예시에서 간단한 2D 데이터셋이 있을 때, 세개의 축을 우리의 초평면 후보로 두었을 때, 실선을 선택하는 방법이 분산을 최대로 보존하는 것이고, c2의 점선을 선택하는 것이 분산을 적게 만들어버리는 방법이다.
다른 방향으로 투영하는 것 보다 분산을 최대로 보존할 수 있는 축을 선택하는 것이 정보를 가장 적게 손실할 수 있다고 생각할 수 있다. 분산이 커져야 데이터들사이의 차이점이 명확해지고, 그것이 모델을 더욱 좋은 방향으로 만들 수 있을 것이기 때문이다.
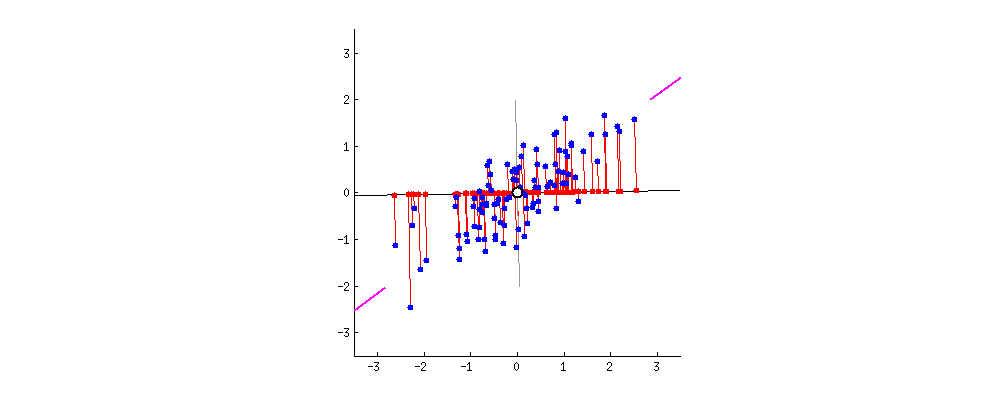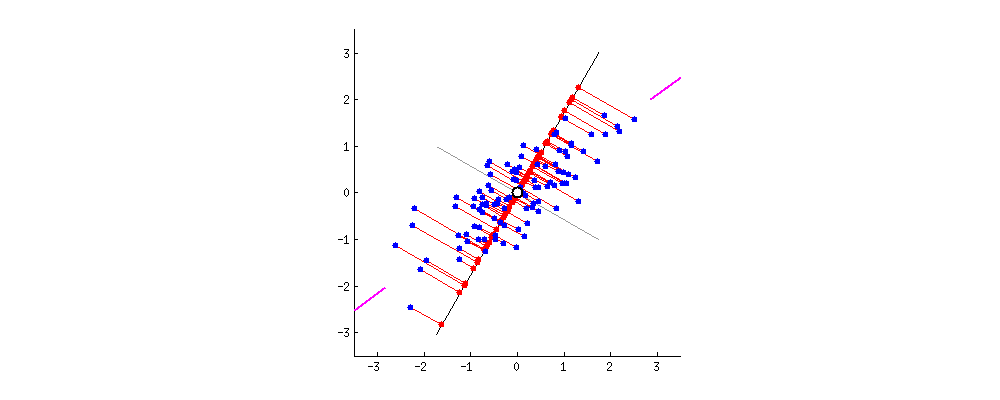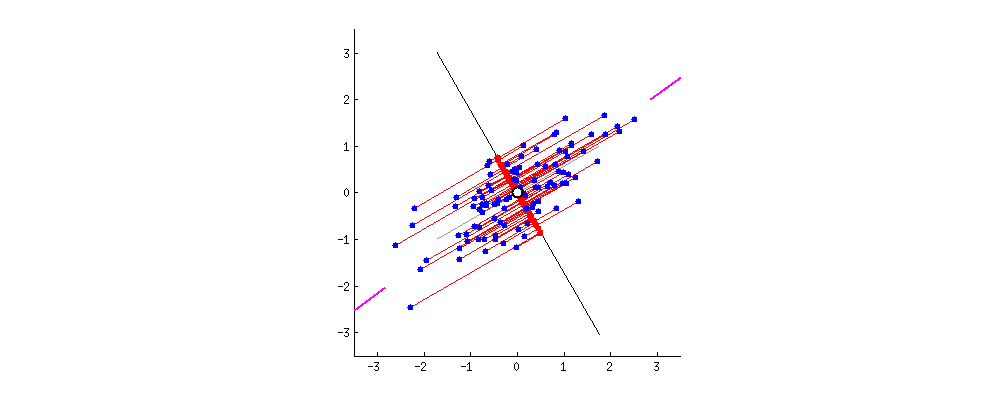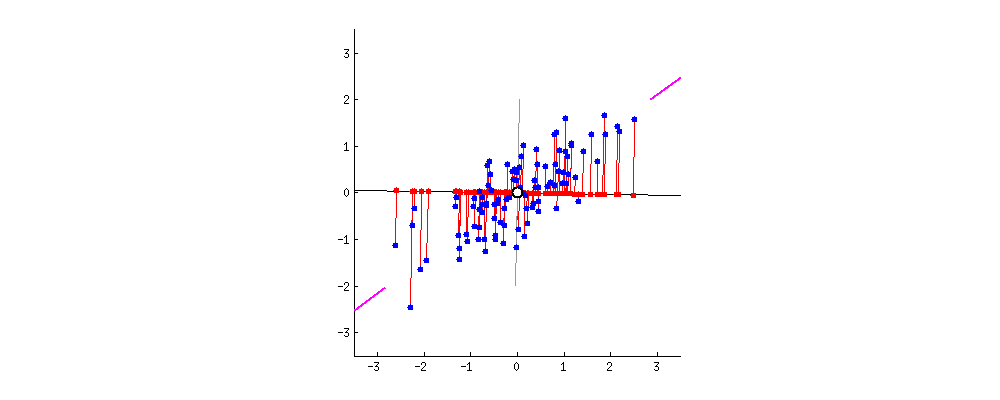
그래서 PCA에서는 분산이 최대인 축을 찾고, 이 첫번째 축에 직교하고 남은 분산을 최대한 보존하는 두번째 축을 찾는다. 2D 예제에서는 선택의 여지가 없지만, 고차원의 데이터셋이라면 여러 방향의 직교하는 축을 찾을 수 있을 것이다.
이렇게 i번째 축을 정의하는 단위 벡터를 i번째 주성분(principal component, PC)라고 한다. 위 예제에서는 첫번째 PC는 c1이고, 두번째 PC는 c2이다.
새로운 장축과 단축을 X축 Y축과 같은 새로운 2차원 평면으로 생각하여 해당 직선에 정사영을 내려 새로운 좌표를 알 수 있다.
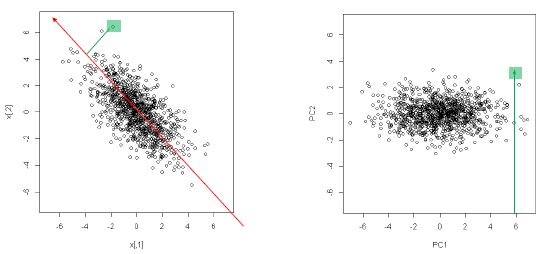
이를 통해서 새로운 데이터의 Boundary를 알 수 있다.
4. PCA의 변수 추출(Feature Extraction)
변수추출(Feature Extraction)은 기존 변수를 조합해 새로운 변수를 만드는 기법으로, 단순히 일부 중요 변수만을 빼내는 변수선택(Feature Selection)과는 대비된다. 변수추출에는 기존 변수 가운데 일부만 활용하는 방식이 있고, 모두 쓰는 방식이 있는데 PCA는 후자에 해당한다. 아울러 PCA는 기존 변수를 선형결합(linear combination)해 새로운 변수를 만들어 낸다.
e.g.) PCA로 변수가 p개, 관측치가 n개 있는 데이터 X(p x n)로 새로운 변수 z를 만드는 과정.
여기에서 벡터 xi는 데이터 행렬 X의 i번째 변수에 해당하는 행벡터(1 x n)인데, 이들을 적절히 조합해 새로운 벡터 zi (1 x n)들을 만들어내는 것이다.
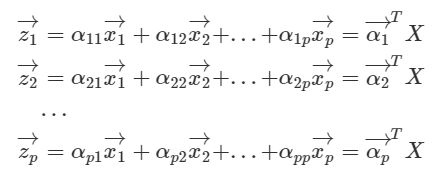
사실 위와 같은 식의 선형결합은 선형변환으로도 이해할 수 있다. 바꿔 말하면 벡터 zi는 X를 αi( p x 1)라는 새로운 축에 사영(projection)시킨 결과물이라는 것이다. 변수추출로 새롭게 만들어진 zi로 구성된 행렬 Z는 아래와 같이 적을 수 있다.
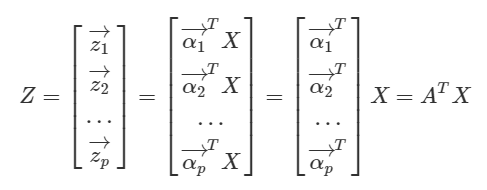
5. Covariance (공분산) 이란?
다시 covariance 부터 알아보면 공분산이라고도 하며, 둘 이상의 변량이 연관성을 가지며 분포하는 모양을 전체적으로 나타낸 분산을 말한다.
공분산은 다음과 같이 구할 수 있다.

또 분포하는 모양에 따라서 다음과 같이 관계를 나눌 수 있다.
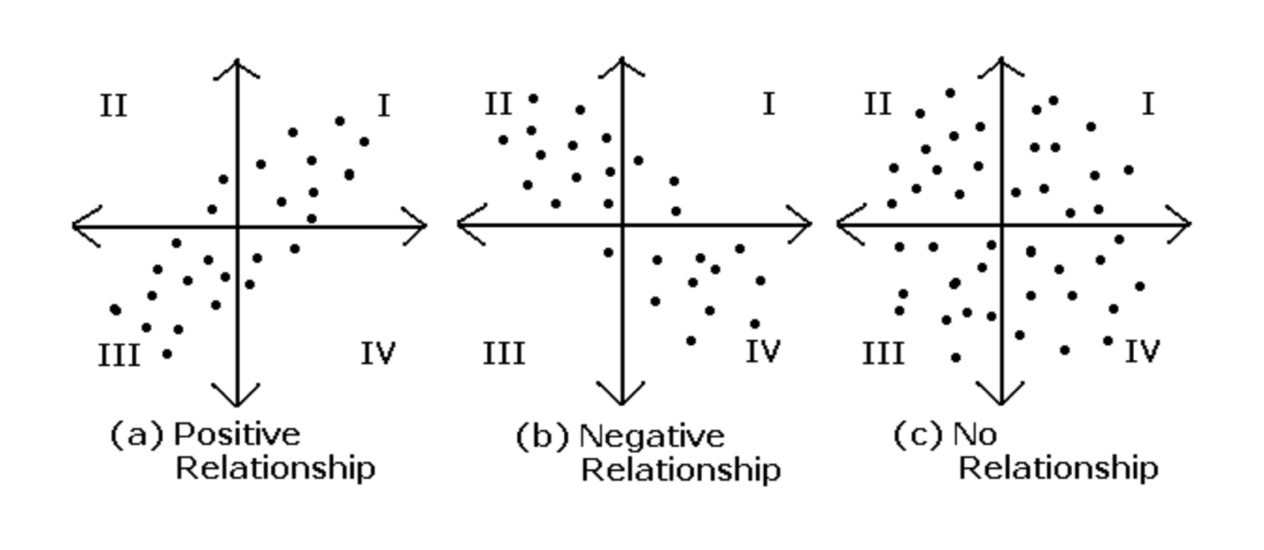
두 확률 변수 X,Y 에 대해
(a) X가 증가할 때 Y도 증가하면 공분산이 0보다 큰 값을 가지며 양의 상관관계에 있다.
(b) X가 증가할 때 Y는 감소하면 공분산이 0보다 작은 값을 가지며 음의 상관관계에 있다.
(c) X와 Y과 연관이 없으면 공분산이 0 값을 가지며 관계가 없다.
6. PCA 수행 과정
1. Mean centering
2. SVD(Singular-value decomposition) 수행
- Scikit-Learn에서 PCA를 계산할 때에도 고유값 분해(eigenvalue-decomposition)가 아닌 특이값 분해(SVD, Singular Value Decomposition)를 이용해 계산한다고 한다.
→ 그 이유는 SVD를 이용하는 것이 계산 속도에 매우 유리하다고 한다.
3. PC score 구하기
- PC score를 활용하여 분석 진행
4. PC score를 설명변수로 활용하여 분석을 진행한다.
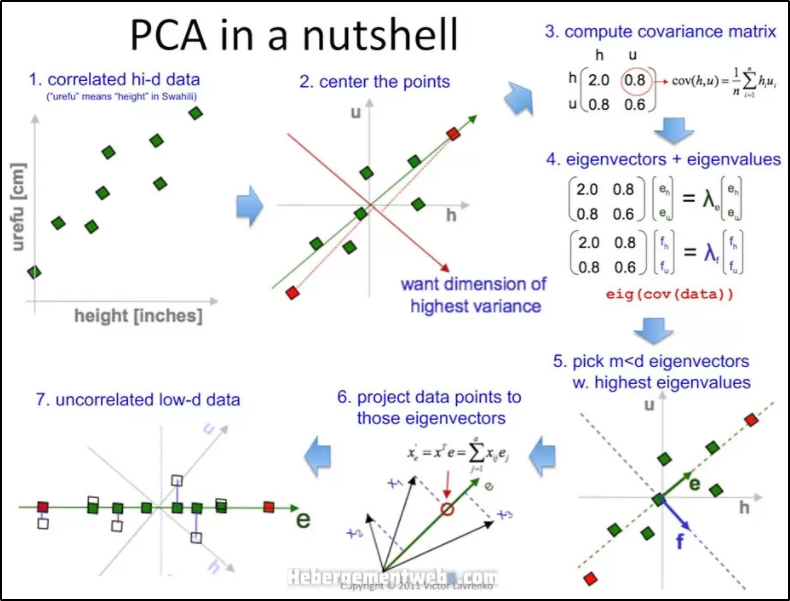
7. Python 코드로 구현
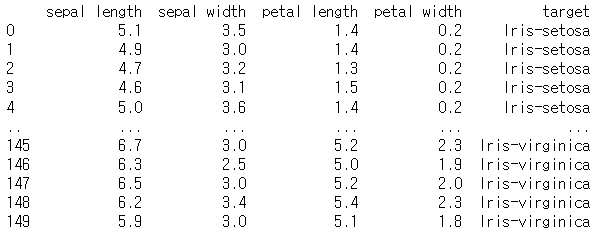
iris.data를 사용하여 구현하였다.
import pandas as pd import matplotlib.pyplot as plt url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data" df = pd.read_csv(url, names=['sepal length','sepal width','petal length','petal width','target']) print(df)
*4가지의 각 컬럼은 '독립변수'이고, target은 종속변수 이다.
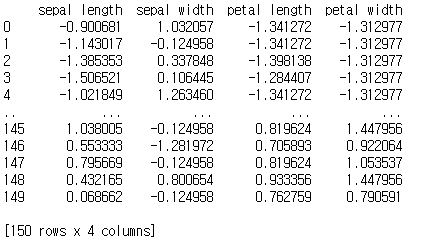
표준화
pca를 하기 전에 데이터 스케일링을 하는 이유는 데이터의 스케일에 따라 주성분의 설명 가능한 분산량이 달라질 수 있기 때문이다.
평균을 빼주고 표준편차로나눠준다.

from sklearn.preprocessing import StandardScaler # 표준화 패키지 라이브러리 x = df.drop(['target'], axis=1).values # 독립변인들의 value값만 추출 y = df['target'].values # 종속변인 추출 x = StandardScaler().fit_transform(x) # x객체에 x를 표준화한 데이터를 저장 features = ['sepal length', 'sepal width', 'petal length', 'petal width'] pd.DataFrame(x, columns=features).head() print(pd.DataFrame(x, columns=features))
작은 고유 값을 같는 경우에는 대부분의 데이터들이 밀접하게 붙어있어서 그 방향으로 별다른 변화량이 없다는 것을 말해 준다.
→ 작은 고유 값을 갖는 차원은 제거해도 된다. (미리 정한 파라미터 값과 비교해서 결정)
→ sklearn의 PCA모델은 자동으로 데이터를 중앙에 맞춰줘서 별도 가공 없이 사용할 수 있다.
각 성분의 설명가능한 분산량을 찾아보았을때, 1번 2번의 성분이 유의미 함을 알 수 있다. (95% 설명가능)
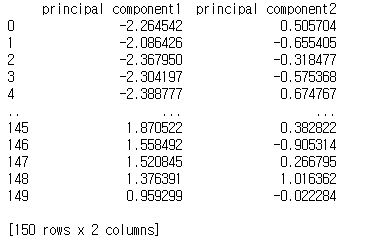
from sklearn.decomposition import PCA #3번 4번 성분은 0.04정도로 설명 가능한 분산량이 얼마 증가하지 않기 때문에, #주성분은 2개로 결정하는 것이 적절하다. #점점 작아지도록 정렬되어 있음을 알 수 있다. pca = PCA(n_components=4) printcipalComponents = pca.fit_transform(x) principalDf = pd.DataFrame(data=printcipalComponents, columns = ['principal component1', 'principal component2', '3','4']) print(pca.explained_variance_ratio_)
pca = PCA(n_components=2) # 주성분을 몇개로 할지 결정 printcipalComponents = pca.fit_transform(x) principalDf = pd.DataFrame(data=printcipalComponents, columns = ['principal component1', 'principal component2']) print(pca.explained_variance_ratio_)
#새로운 공간에 투영하고 나면 원래의 변수들이 사라짐. #PC1, PC2이라는 축이 존재할 뿐, 더 이상 'sepal length'이나 'sepal width' 같은 이름을 붙일 수가 없다. print(principal_components) #주성분으로 이루어진 데이터 프레임 구성
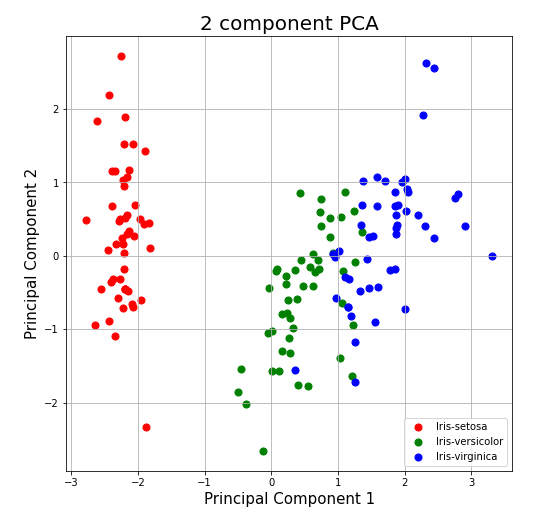
import matplotlib.pyplot as plt fig = plt.figure(figsize = (8, 8)) ax = fig.add_subplot(1, 1, 1) ax.set_xlabel('Principal Component 1', fontsize = 15) ax.set_ylabel('Principal Component 2', fontsize = 15) ax.set_title('2 component PCA', fontsize=20) targets = ['Iris-setosa', 'Iris-versicolor', 'Iris-virginica'] colors = ['r', 'g', 'b'] finalDf = pd.concat([principalDf, df[['target']]], axis = 1) for target, color in zip(targets,colors): indicesToKeep = finalDf['target'] == target ax.scatter(finalDf.loc[indicesToKeep, 'principal component1'] , finalDf.loc[indicesToKeep, 'principal component2'] , c = color , s = 50) ax.legend(targets) ax.grid()
*축이 데이터의 방향에 맞게 설정되어 있다면 균등하게 떨어질 것이고, 잘 설정되어 있지 않았다면 축에 떨어질때 겹치는 부분이 많을 것이다.
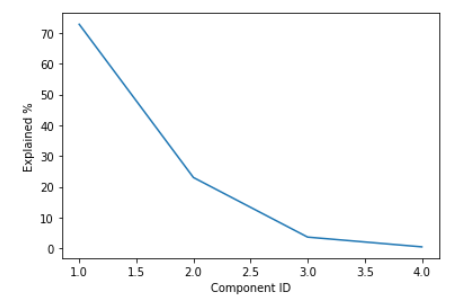
컴포넌트의 설명률 (PC1, PC2, ... 순서대로 계속 작아지는 게 정상)
pca_all = PCA(n_components=4) pca_all.fit(x) print(pca_all.explained_variance_ratio_) # 각 컴포넌트의 설명률 (PC1, PC2, ... 순서대로 계속 작아지는 게 정상) # PC3 이후로는 설명률이 10% 미만이다. plt.plot(np.arange(1, 5), pca_all.explained_variance_ratio_ * 100) plt.xlabel("Component ID") plt.ylabel("Explained %")
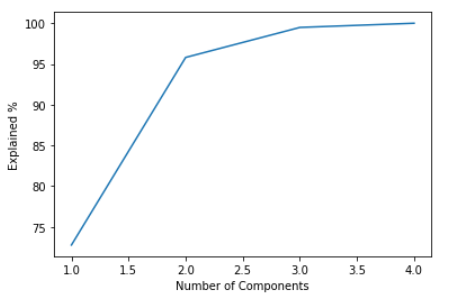
컴포넌트 개수에 따른 누적 % (점점 둔하게 증가)
PC1부터 PC2까지 2개의 컴포넌트만 있어도 전체 분산의 약 95%를 설명할 수 있다는 뜻.
plt.plot(np.arange(1, 5), np.cumsum(pca_all.explained_variance_ratio_) * 100) plt.xlabel("Number of Components") plt.ylabel("Explained %")
출처 : https://ssungkang.tistory.com/entry/%EC%9D%B8%EA%B3%B5%EC%A7%80%EB%8A%A5-PCA-1-Principle-Component-Analysis-%EB%9E%80?category=324327
https://butter-shower.tistory.com/210
https://m.blog.naver.com/tjdrud1323/221720259834
https://ratsgo.github.io/machine%20learning/2017/04/24/PCA/
https://chancoding.tistory.com/52
수식 부분은 잘 이해하지 못하는지라 추가하지 않았습니다.
생초보라... 잘못된 내용이 있을 경우 알려주시면 감사하겠습니다.🐻