다른 변수에 영향을 받지 않는 독립적인 변수를 독립 변수,
다른 변수에 영향을 받는 변수를 종속 변수라고 하는데,
함숫값을 결정할 때 2개 이상의 독립 변수가 필요한 함수를 다변수 함수라고 한다.
w=f(x, y, z, ...)와 같은 형태로 쓰는데, 이러한 다변수 함수를 미분할 때 사용하는 것이 편미분과 전미분이다.
1. 편미분이란?
편미분은 다변수 함수에서 관심이 있는 한 변수만 변수로 생각하고, 나머지 변수들은 상수로 취급한 뒤 미분하는 방법이다.
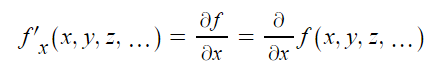
어떤 함수를 미분한 함수를 도함수라고 했듯이, 어떤 함수를 편미분한 함수를 편도함수라고 한다. 편도함수를 나타내는 방법도 일반적인 도함수를 나타내는 방법과 비슷하지만, 도함수와 구분해야 하고, 여러 변수 중 어떤 변수만 변수로 취급하고 미분했는지 표시해야 하기 때문에 f'x(x, y, z, ...), ∂f/∂x와 같은 표현을 사용한다. 편미분을 할 때는 미분 연산자가 ∂f/∂x와 같이 d 대신 ∂를 사용한다.
이 문자는 그냥 d라고 읽으면 된다.
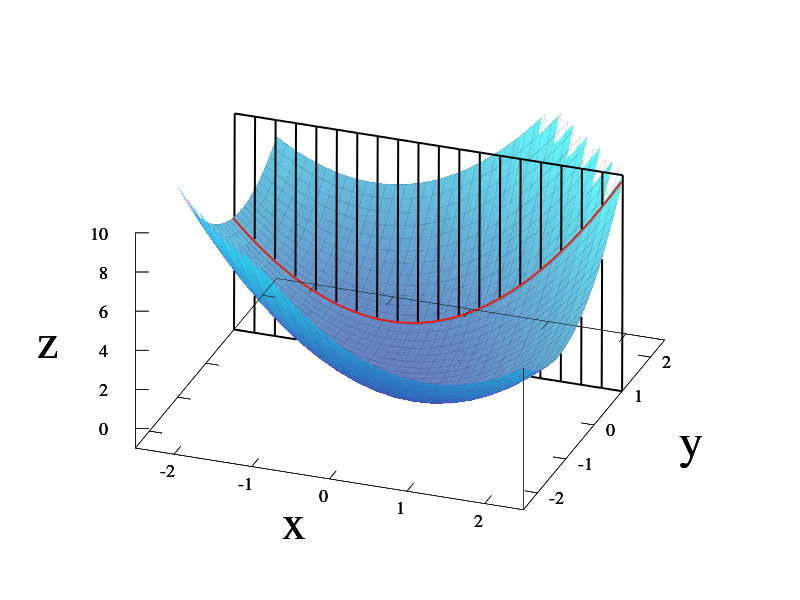
1변수 함수는 그래프 위 하나의 점을 고르면 1개의 접선만 존재하지만, 다변수 함수는 무수히 많은 접선이 존재합니다. 수많은 접선 중 하나의 접선의 기울기(순간변화율)만을 구하기 위해 하나의 변수를 제외한 다른 변수의 값을 상수로 취급, 즉 값을 고정한 뒤 미분을 하는 것이 바로 편미분이다.
위 3차원 그래프는 z=x^2+xy+y^2라는 함수의 그래프인데, y=1로 고정했을 때 절단면이 바로 빨간색 곡선입니다. 저 빨간색 곡선에서 접선의 기울기를 구하는 것이 바로 x에 대한 z의 편미분이다.
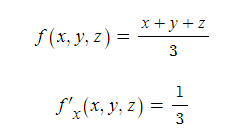
여기서 x에 대한 편미분을 구하면 다음과 같다. 마치, y는 상수처럼 취급해서, y의제곱은 상수니깐, 그냥 0이 된다. x의 제곱은 2x가 되고, xy에서 y는 상수취급이 되니, y만 남게 되어 아래와 같이 된다.
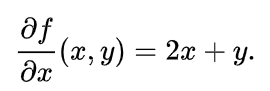
y에 대한 미분의 경우에는 반대로 x를 상수치급해서 y에 대해서만 미분을 계산하면 된다.
예제 : 간단한 예제를 통해서 어떻게 편미분을 계산하는지 살펴보자. 다음과 같은 x, y 두 변수로 이루어진 함수 f가 있다고 하자.
여기서 x에 대한 편미분을 구하면 다음과 같다. 마치, y는 상수처럼 취급해서, y의제곱은 상수니깐, 그냥 0이 된다. x의 제곱은 2x가 되고, xy에서 y는 상수취급이 되니, y만 남게 되어 아래와 같이 된다.
y에 대한 미분의 경우에는 반대로 x를 상수치급해서 y에 대해서만 미분을 계산하면 된다.
2. 전미분이란?
편미분은 주로 다변수함수에서 1개의 변수의 값이 변화할 때의 변화율을 알기 위해 활용되는데, (x, y, z)라는 3개의 시험 과목의 평균을 구하는 함수 f를 가정해보자.
이때 x라는 과목의 점수만 변화했을 때 전체 평균이 얼마나 변할지 궁금할 때 함수 f를 x에 대해 편미분하면 된다. x 과목이 1점 떨어질 때마다 평균이 0.3점씩 떨어지는 것을 알 수 있다.
그렇다면 x, y, z 과목의 점수가 모두 변화할 때 전체 평균이 어떻게 변하는지 알고 싶다면, 즉 다변수 함수를 모든 변수에 대해 미분하고 싶다면 어떻게 하면 될까?
이 때 전미분을 사용하게 된다.
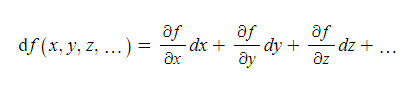
전미분은 각각의 변수에 대한 편미분을 구한 뒤 모두 더하면 된다. 이때 dx, dy, dz, ...는 증분, 즉 변화량을 말한다. 이렇게 함수를 전미분 한 함수를 전도함수라고 하고, 모든 변수에 대해 미분하는 것이기 때문에 특별한 변수 표기 없이 바로 함수 이름 앞에 d를 붙임으로써 전도함수를 표현한다.
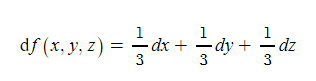
위의 평균 구하는 함수를 전미분하면 위와 같다. 만약 x 과목의 점수가 6점, y 과목의 점수가 12점, z 과목의 점수가 30점 떨어졌다면 평균이 총 2+4+10=16점 떨어지게 된다.
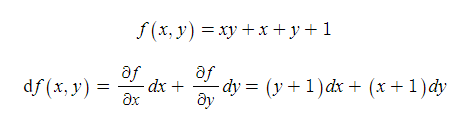
위 함수를 전미분하면 이렇게 된다.
출처 :
https://m.blog.naver.com/kmc7468/221898862253
https://m.blog.naver.com/sw4r/221946248471
https://en.wikipedia.org/wiki/Partial_derivative

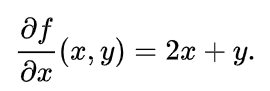
안녕하세요 글 잘 보고 있어요..!
제가 요즘 많이 고심하는데도 모르겠어서
여쭤보고 싶은 공업수학 문제가 있는데
혹시 답변 해주실 수 있으실까요..?
곤란 하시다면 답변 안 해주셔도 괜찮아요
문제는 이거예요…!
“분리가능 상미분 방정식은 양형태 상미분 방정식의 일부이고, 완전 상미분 방정식은 음형태 상미분 방정식 일부라고 볼 수 있다.
양형태의 상미분 방정식 중 분리가능한 상미분 방정식을 제외하고 남은 상미분 방정식들은 어떤 것들이 있는지 (즉, 분리가능하지 않은 상미분 방정식들), 음형태의 상미분 방정식 중 완전 상미분 방정식을 제외하고 남은 상미분 방정식들은 어떤 것들이 있는지 (즉, 완전하지 않은 상미분 방정식들) 쓰시오.
즉.
양형태의 상미분 방정식의 전체 집합을 W.
음형태의 상미분 방정식의 전체 집합을 U,
분리가능한 상미분 방정식의 전체 집합을 A,
완전 상미분 방정식의 전체 집합을 B
라고 할 때
집합 A^c ᑎ W 과 집합 B^c ᑎ U 에 대해 기술하는 문제이다. 그 집합에 해당하는 미분 방 정식의 예를 몇 개 구하고 그들의 공통된 특징을 기술하는 방법을 써도 좋고, 아니면 이 집 합에 속하는 방정식들의 특징을 바로 기술하여도 좋다.“