그래픽 과제로 무엇을 할까 고민을 하다가 프랙탈 과제를 선택하였다.
3개 중에 가장 복잡해 보이지만 코드의 구성은 생각보다 간단하고, 문제가 수학 공식을 좀 이해를 해야 한다는 것이 문제다.
그럼 프랙탈이 무엇인지 알아보자.
1.프랙탈이란?
부분이 전체와 닮고, 전체가 부분에서 비롯되는 현상
: “혼돈속에 질서가 있다(카오스 이론)”에서 시작해서 부분이 전체 구조와 일치한다는 것을 알게 되었다.
자연을 설명하기 위해서 만들어낸 법칙임.(눈의 결정체, 산, 나무의 형체 등등)

프랙탈 설명 Link ▼
https://namu.wiki/w/%ED%94%84%EB%9E%99%ED%83%88%20%EC%9D%B4%EB%A1%A0
1)프랙탈의 특징은?
-.일반적으로 자기 유사성을 가지고 있음.
-.반복 작업을 통해 만들어짐
-.무한하게 세분화 됨
-.길이가 무한함
프랙탈에 대해서 좀 더 쉽게 알고 싶으면 아래의 안될과학 유튜브를 추천한다.
https://www.youtube.com/watch?v=1uY-IwdL-yI
2.과제 요구사항
: 요구사항이 이전에 비해 많이 간단해진 것 같다.
-.mandatory
1.프랙탈인 julia와 Mandelbrot집합을 만들어야 한다.
2.마우스 휠로 무한대로 확대 및 축소가 가능해야함(컴퓨터의 한계 내에서)
3.프랙탈의 깊이를 표시하기 위해서 색상을 이용해야 함(색 표시하라는 뜻)
4.매개변수 처리해야함(julia만 매개변수를 이용한다. 나머지는 무시하는 예외처리를 해야함)
5.매개변수로 julia 집합을 생성할 수 있어야 함.
6.esc로 프로그램을 종료해야함
7.minilibX라는 그래픽 라이브러리로 이 과제를 수행하면 된다.
(다른 라이브러리로 해도 되지만 여기서는 이것을 추천한다.)
-.bonus
1.위의 두개의 프랙탈 말고 하나의 프랙탈을 골라서 만든다.
2.마우스로 확대/축소를 할때 마우스의 지점에서 확대/축소가 일어나야 한다.
(마우스의 위치가 아닌 곳에서 확대/축소가 일어나면 안된다.)
3.화살표로 이동이 가능해야 한다.
4.색상 범위를 이동해야 한다.(간단히 말하면 보고 있는 색 말고 다른 색을 표현하라는 뜻)
3.과제를 하기 위해 공부해야 하는 것
1.mlx사용법
: miniLibX라고 하는 그래픽 라이브러리의 사용법을 공부해야 한다.
생각보다 그렇게 어렵지는 않고, 어떤 것이 들어가고 리턴 값이 무엇이고 실패하면 어떤 것을 반환하는지 등등을 공부하면 된다.
: mlx의 사용법은 아래에 잘 나와있어서 링크를 첨부한다.
2.프랙탈 공식 이해
: 이해를 완벽하게 하려면 너무 어렵지만 그래도 이 과제는 이 공식을 이해하는 편이 좋다.
공식을 이해하다 보면 결국 X^2 + Y^2 < 4라는 간단한 결론에 이르게 된다.
하지만 아래의 링크를 통해 프랙탈의 공식에 대해서 조금 이해를 해보자.
https://pkjung.tistory.com/142
4.프로그램 구성
: 프로그램을 어떻게 구성했는지 간단하게 적어 보았다.
◼︎ 기본 영역
1)예외처리
2)mlx시작 하는 영역
-.mlx 시작하기
-.window 창 만들기
-.image 시작하기
-.img pointer의 주소가져오기
3)프랙탈을 계산하는 영역
4)가져온 image pointer 주소에 색상 넣기
5)넣은 image를 출력하는 영역
이 부분까지가 기본적인 구성의 끝이다. 아래의 부분은 프로그램이 실행될때 우리가 input을 주면 반응을 한다.
◼︎ input이 들어오면 처리해주는 영역
6)키 읽기
7)마우스 읽기
◼︎ input에 따라 변경하는 영역
8)줌
9)색상 바꾸기
10)종료
5.어려웠던 부분
1.다른 부분들은 위의 링크들을 통해서 쉽게 도달할 수 있지만, 보너스 부분의 줌을 마우스 좌표에서 계속 들어가는 부분은 쉽지가 않다. 이유는 좌표계에 대해서 우리가 고민을 해야 하기 때문이다.
-.확대/축소를 처리하기 위한 좌표계의 이해
: 만약 마우스의 좌표를 화면의 우측 위쪽에 확대를 했다고 하면 주황색 영역이 확대가 된다.
실제 좌표계로 봤을때는 저 작은 영역이 확대가 되는 것이다. 그렇게 되면 쓰지 않게 되는 남는 영역이 발생되게 되고, 이 영역을 프랙탈을 계산할때 offset으로 주면 우리는 마우스의 좌표를 기준으로 계속 확대를 할 수가 있다.
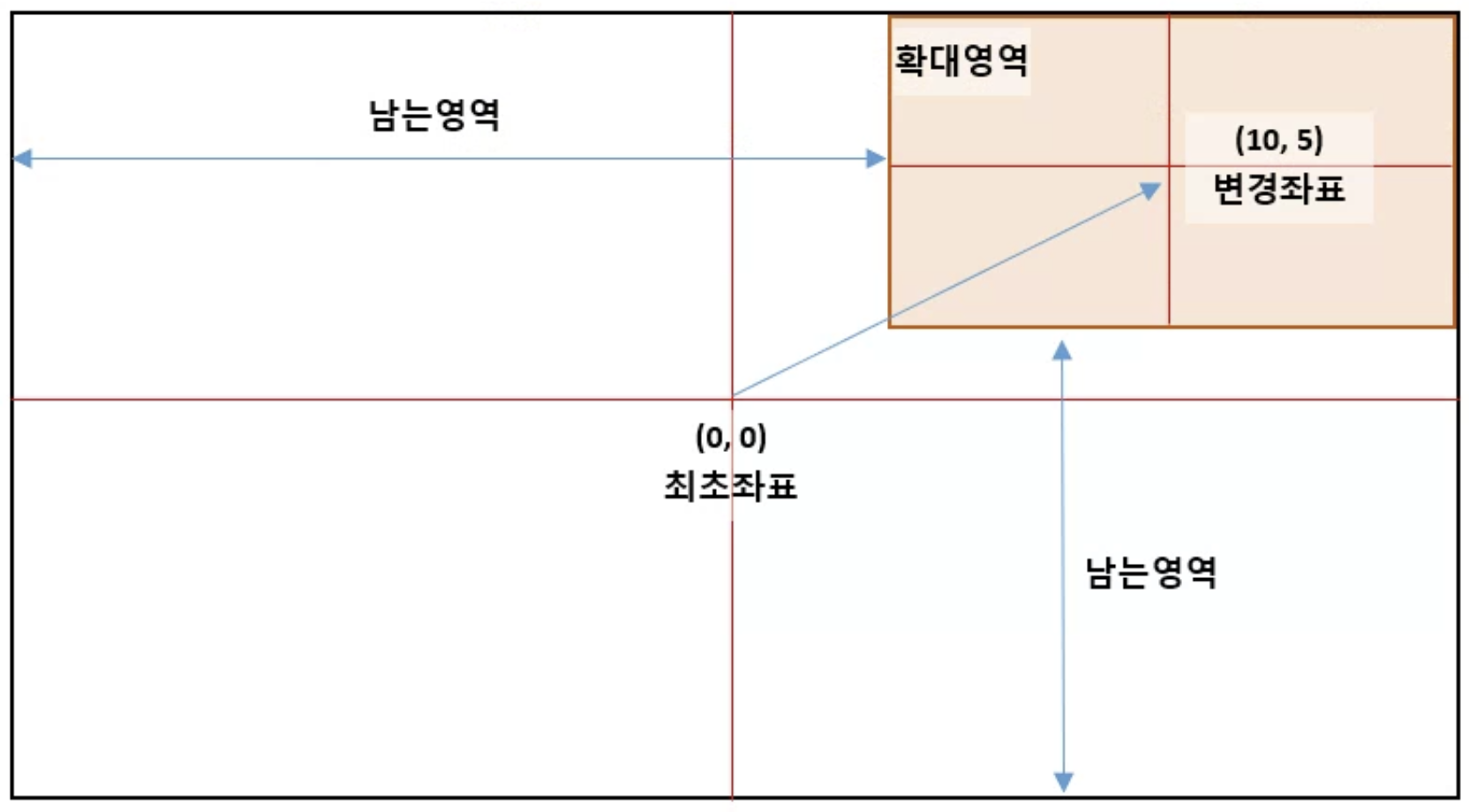
간단히 이 부분만 코드를 살펴보자.
아래의 코드를 보면 c.re(실수 부분), c.im(허수 부분)을 계산한 부분이 있다.
t_complex screen_to_complex(int count_x, int count_y, t_viewpoint *vp)
{
t_complex c;
c.re = ((double)count_x / W_WIDTH * (vp->xmax - vp->xmin)) * vp->zoom + vp->xmin + vp->offx;
c.im = ((double)count_y / W_HEIGHT * (vp->ymax - vp->ymin)) * vp->zoom + vp->ymin + vp->offy;
return (c);
}
t_viewpoint *init_viewpoint(t_viewpoint *vp)
{
vp->offx = 0.0;
vp->offy = 0.0;
vp->xmax = -2.0;
vp->xmin = 2.0;
vp->ymax = 1.0;
vp->ymin = -1.0;
vp->zoom = 1.0;
return (vp);
}c.re의 식을 살펴보면
count_x : 실제로 우리가 윈도우를 800 X 600(Width x Height)로 만들었다고 하면 그 범위내의 x축의 한 픽셀의 영역이라고 생각하면 된다.(Width를 800으로 했으면 0부터 799까지임)
W_WDITH : 위에서 말한 Width이다.(800을 말함)
vp->xmax : 현재 확대된 창의 범위내에서 가장 큰 x의 수(복소수 좌표계에서 말하는 것임)
vp->xmin : 현재 확대된 창의 범위내에서 가장 작은 x의 수(복소수 좌표계에서 말하는 것임)
vp->zoom : 현재 줌의 상태를 곱해준다(최초에 1로 시작한다)
vp->offx : 위의 그림에서 남는 영역을 계속 합해준 것을 offset 처리해준다.
count_x / W_WIDTH : 실제 윈도우 창과 복소수 좌표의 비율을 조정
(vp->max - vp->xmin) : 현재 확대된 영역의 전체 x길이
zoom : 현재 줌의 상태를 곱해준다.
여기까지가 확대된 창을 만든다고 생각하면 된다.
+vp->xmin : 확대된 창을 시작위치로 이동시켜준다.
+vp->offx : 이번 확대 뿐 아니라 그 이전까지의 offset까지 반영해서 처리해준다.
식을 말로 설명하는게 생각보다 쉽지 않은 것 같다.
혹시 보시다가 궁금한 점이 있으면 댓글 남겨주시면 감사하겠습니다.
6.회고
1.프로그램 구성은 간단하였으나 생각보다 쉽지는 않다.
: 프랙탈의 공식을 이해하는게 처음에는 좀 힘들었다.
: 좌표계를 이해하기 위해서 고민이 많았다. 여기저기 찾아보았는데 제각기 다른 방식이어서 힘들었던 것 같다.
차라리 한번 고민을 해보고 만들어보는 쪽도 추천을 한다.
: mlx의 사용법은 간단하나 확실한 사용법인지 의문이 좀 갔다.
: mlx의 창을 esc가 아닌 x를 눌러서 종료하면 꺼지지 않는 문제가 생기기 때문에 따로 처리를 해주어야 한다.(아래 참조)
mlx_hook(mlx->win_ptr, 17, 0, terminate_fractol, mlx);2.예외처리는 어딜가나 중요하다고 생각이 들었다.
: 다행인지 push_swap을 진행하고 이 과제를 해서 그런지 예외처리에 대해서 조금 더 신중해지고 테스트 케이스가 많이 생각이 났다.
: julia 공식은 숫자를 int형이 아닌 double이나 float로 받아주어야 한다. 나의 경우 double로 받아서 atod라고 새롭게 하나 만들어 주었다.
3.Makefile은 여전히 어렵다.
: 알듯 말듯한 이 느낌은 무엇인지 모르겠다.
그래도 이번에 조금이라도 더 안거 같고, 처음에 시작할때부터 만들어서 했더니 더 편하게 과제를 할 수 있었다.
