ML - 1. IRIS 분류

솔비·2024년 2월 19일
MLstudy note
0

🤖 ML / DL

목록 보기
1/6
post-thumbnail

Machine Learning

자동으로 데이터에서 규칙을 학습하는 알고리즘을 연구하는 분야
대표적인 라이브러리로 사이킷런이 있다.

📢 오늘 공부 목표




iris data 탐색

(1) 데이터 불러오기

# 머신러닝 공부 데이터
from sklearn.datasets import load_iris

iris = load_iris()

(2) 데이터 확인

  • iris 품종확인

  • 각각의 target

    • 0 : setosa
    • 1 : versicolor
    • 2 : virginice

  • 데이터 정보

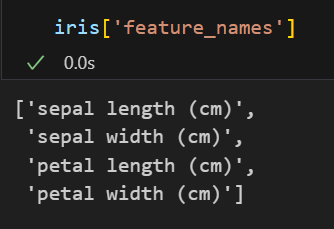
  • 150가지의 iris 데이터

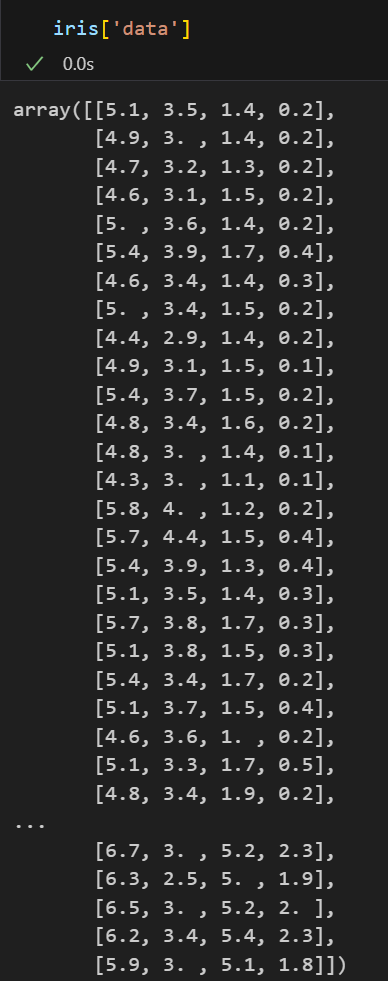
(3) 데이터프레임화

import pandas as pd

iris_pd = pd.DataFrame(iris['data'], columns = iris['feature_names'] )
iris_pd['species'] = iris['target']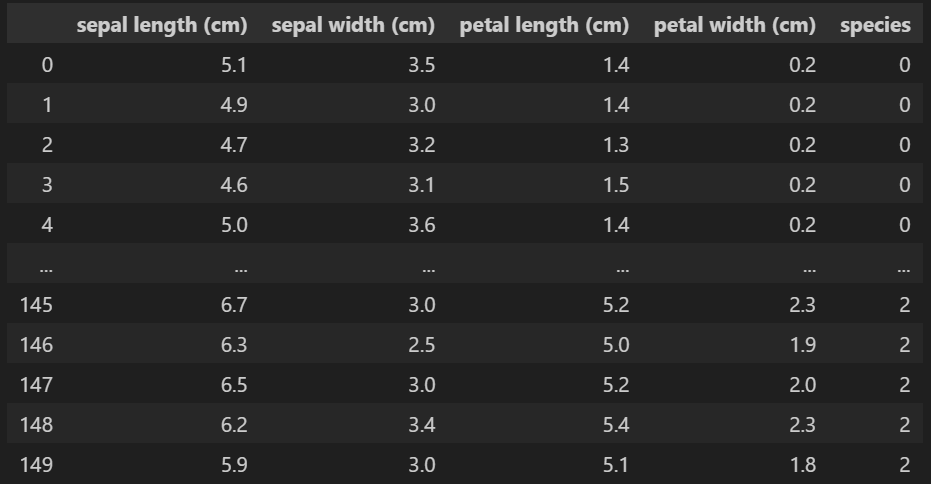


어떻게 하면 세 품종을 구분할 수 있을까 ?

(4) 시각화 확인

  • 모듈 import
import matplotlib.pyplot as plt
import koreanize_matplotlib
import seaborn as sns

각 컬럼별 boxplot

  • sepal length
     plt.figure(figsize=(12,6))
 sns.boxplot(x='sepal length (cm)', y='species', data = iris_pd, orient='h')
    📌 각 box가 겹쳐있어 구분하기 애매함

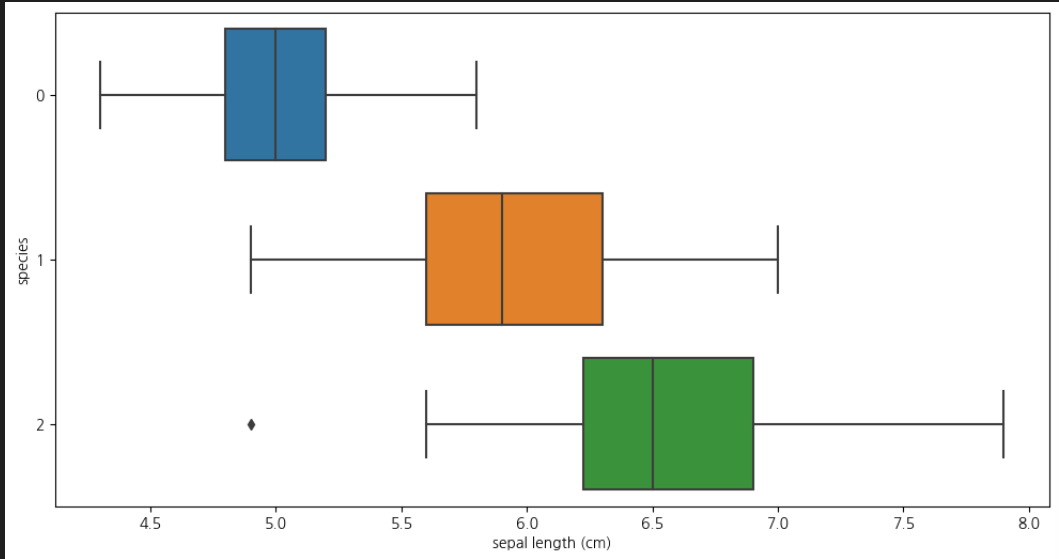
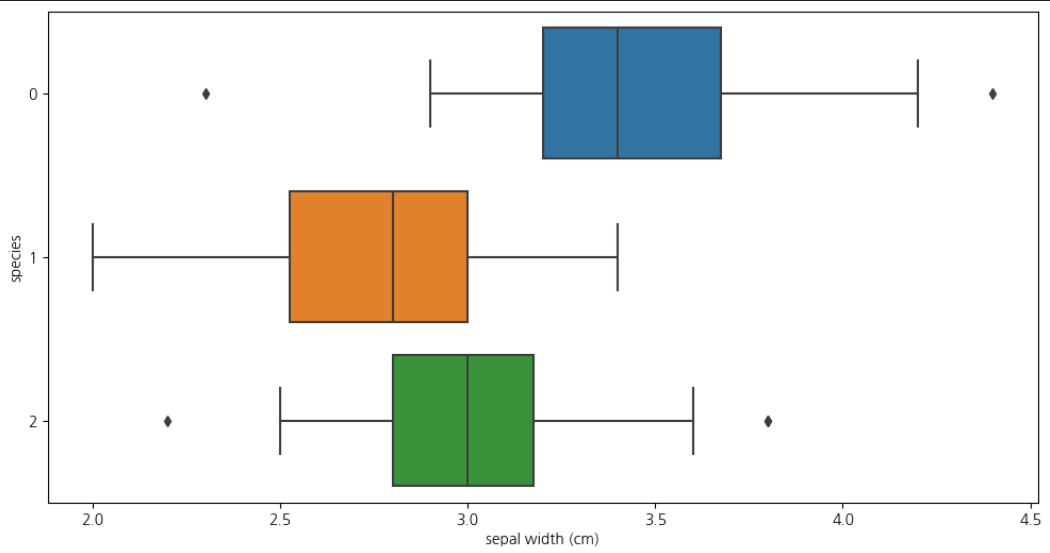
  • sepal width

    plt.figure(figsize=(12,6))
sns.boxplot(x='sepal width (cm)', y='species', data = iris_pd, orient='h')

    📌 각 box가 겹쳐있어 구분하기 애매함

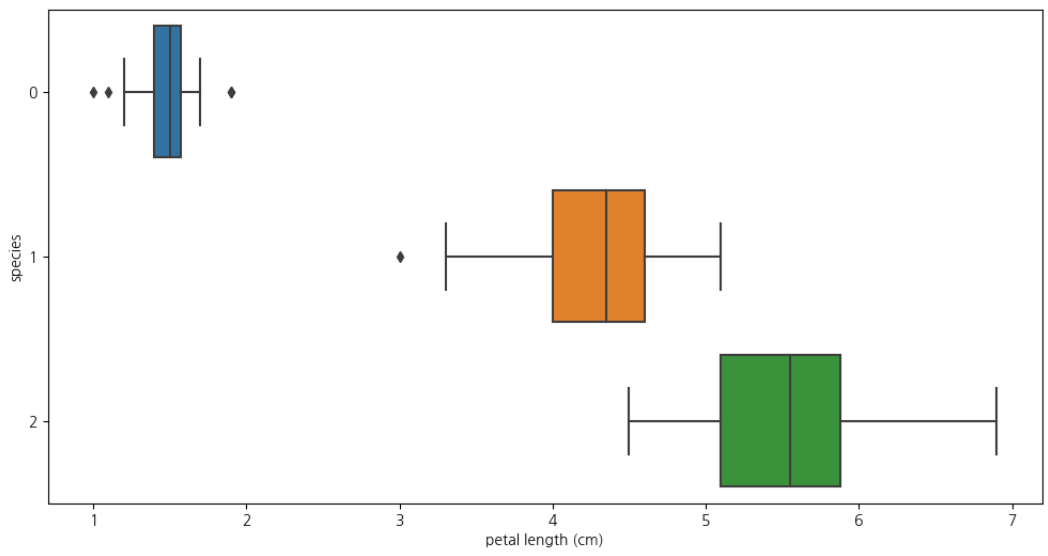
  • petal length & petal width
    📌 setosa에 해당하는 0번품종은 구분가능

    plt.figure(figsize=(12,6))
sns.boxplot(x='petal length (cm)', y='species', data = iris_pd, orient='h')

plt.figure(figsize=(12,6))
sns.boxplot(x='petal width (cm)', y='species', data = iris_pd, orient='h')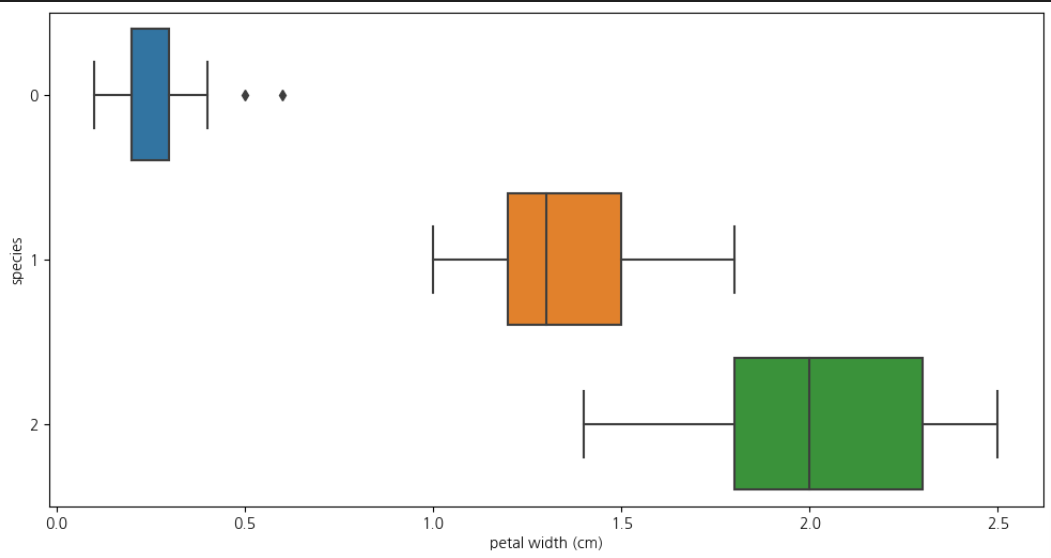


pairplot

구분되는 그래프가 있는지 확인하기

sns.pairplot(iris_pd, hue='species')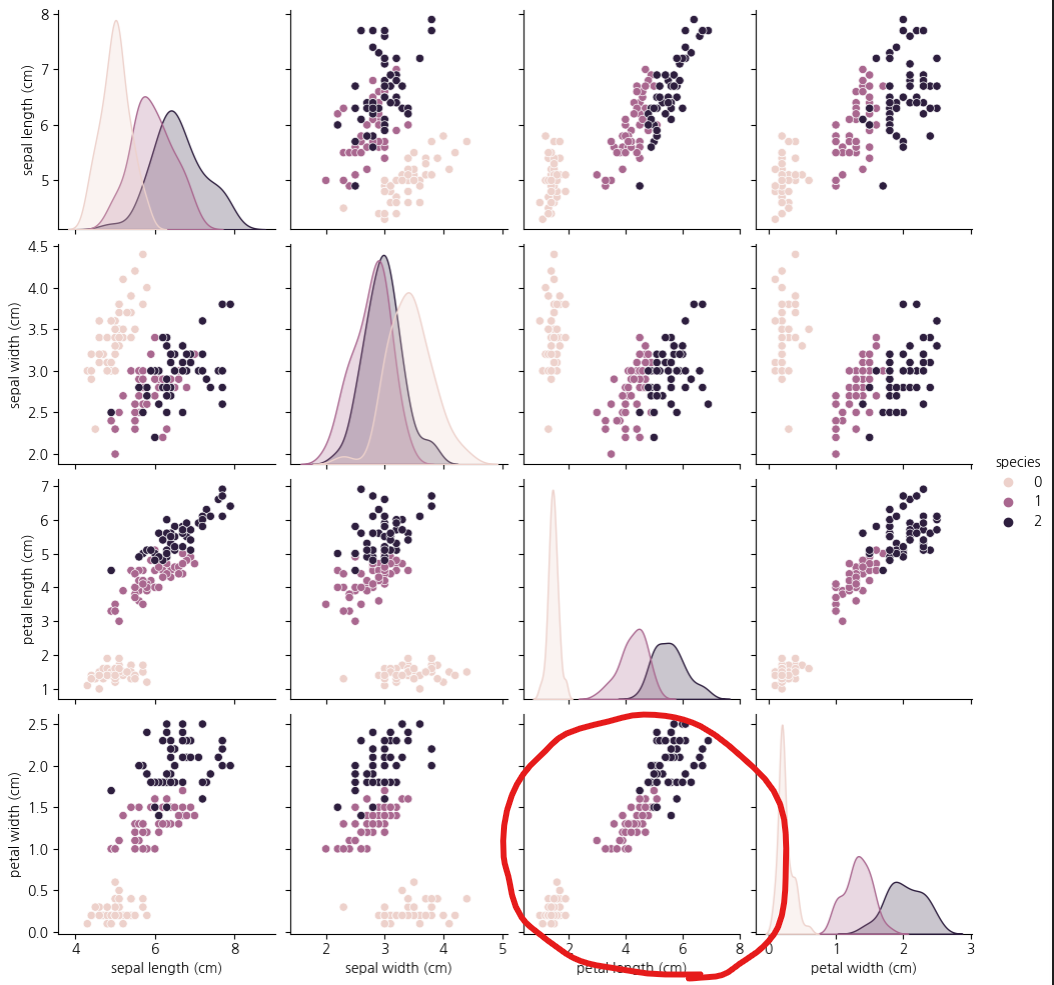

sns.pairplot(data=iris_pd,
             vars=['petal length (cm)','petal width (cm)' ],
             hue='species', height=4)

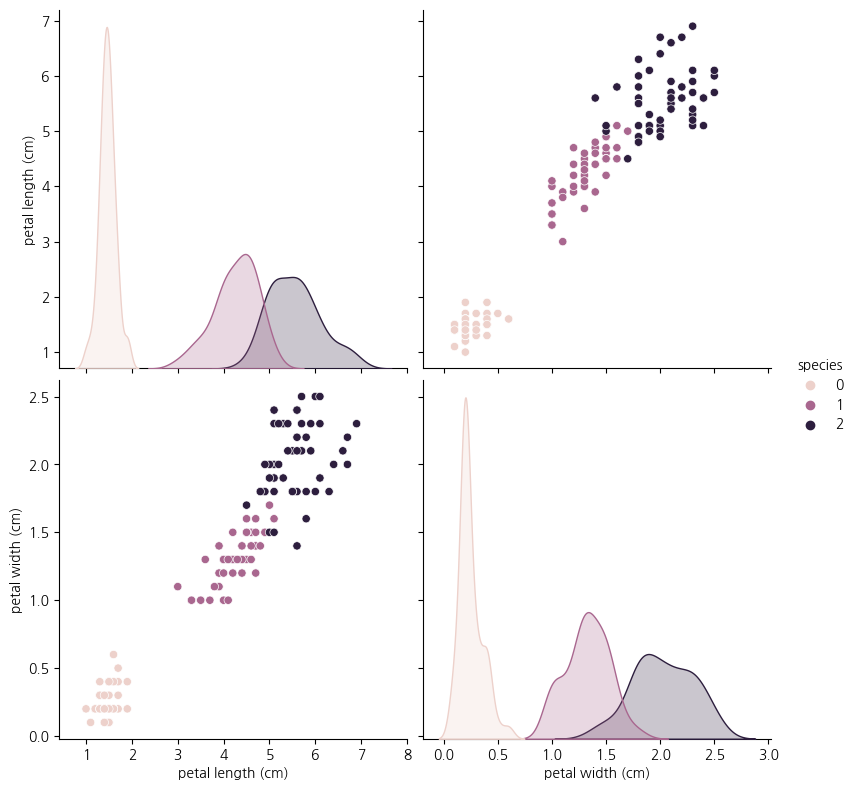
위 그래프를 볼 때 0번 품종은 분류가능할 것으로 보인다.
ex) petal length가 2.5보다 작으면 setosa





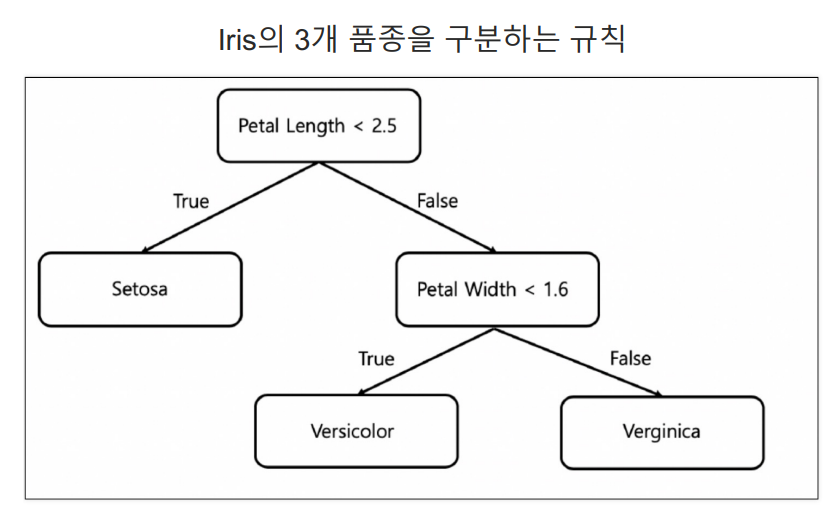
1. Decision Tree

나머지 1번 2번 품종 분류를 해보자


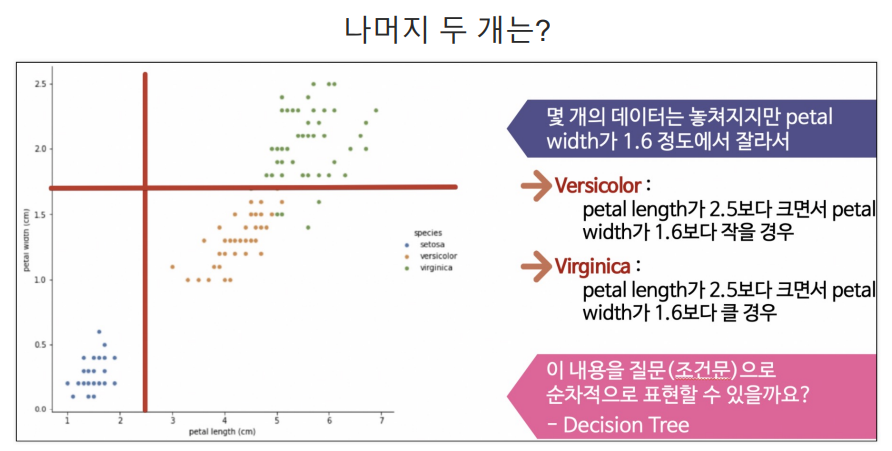
  • 1번 2번 품종 데이터만 보기
iris_12 = iris_pd[iris_pd['species'] != 0]

plt.figure(figsize=(12,6))
sns.scatterplot(x='petal length (cm)', y='petal width (cm)',
                data=iris_12, hue='species', palette='Set2')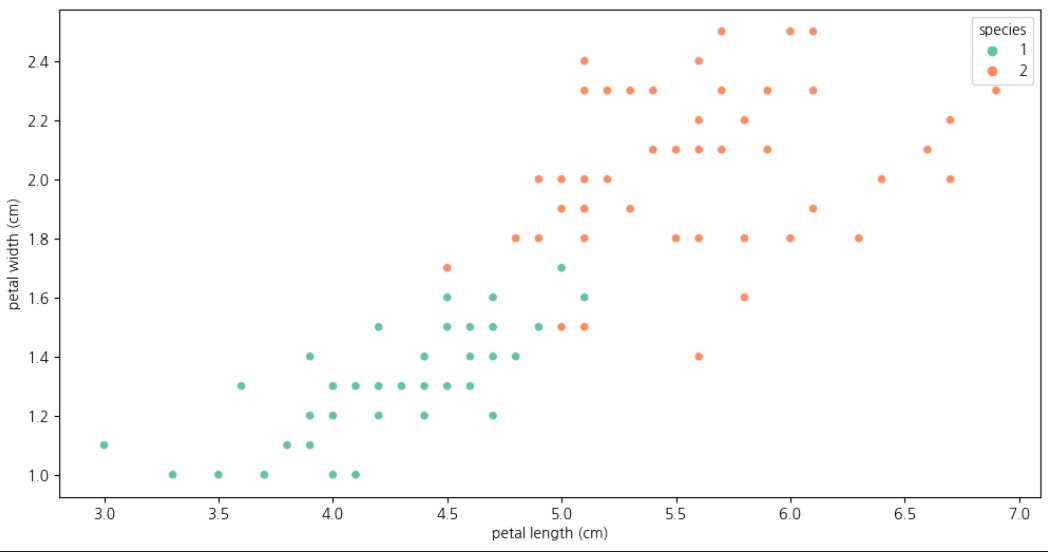




이 때, 구분선이 어디에 있어야 최선일까 ?

🚩 Split Criterion (분할기준)



(1) 엔트로피 개념


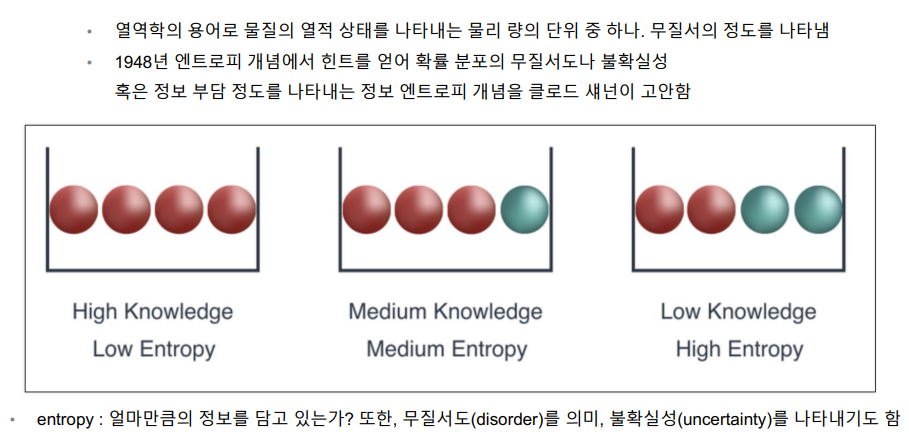
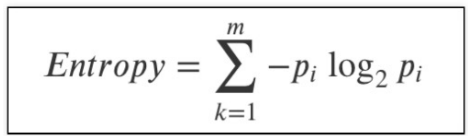
📌 엔트로피 = (-pi log2 pi)의 모든 합

무질서할수록 엔트로피 값은 높다 (불확실 성이 높을 수록)
엔트로피 값이 내려갈수록, 질서가 잡혀가는 것!!!

(1)-1 예제

📌 기본

파란공(10개) 빨간공(6개)
-(10/16)np.log2(10/16) - 6/16np.log2(6/16)
0.954434002924965
📌 정 중앙에 선을 하나 만들어서 나눔

(왼쪽) 파란공(1) 빨간공(7), (오른쪽) 파란공(5) 빨간공(3)

0.5*(-(7/8)*np.log2(7/8) -1/8*np.log2(1/8)) + \
0.5*(-(3/8)*np.log2(3/8) - 5/8*np.log2(5/8))
0.7489992230622807

✅
엔트로피가 내려갔으므로, 분할 하는 것이 좋음!!!!



(2) 지니계수

Gini index 혹은 불순도율
엔트로피의 계산량이 많아서 비슷한 개념이면서 보다 게산량이 적은 지니계수를 사용하는 경우가 많다.

(2)-1 예제

📌 기본

파란공(10개) 빨간공(6개)

# 1 - 파란색의 확률 - 빨간색의 확률
1 - (6/16)**2 - (10/16)**2

0.46875
📌 정 중앙에 선을 하나 만들어서 나눔

(왼쪽) 파란공(1) 빨간공(7), (오른쪽) 파란공(5) 빨간공(3)

0.5*(1 - (7/8)**2 - (1/8)**2) + 0.5*(1 - (3/8)**2 - (5/8)**2)

0.34375
✅
지니계수 값이 내려갔으므로, 분할 하는 것이 좋음!!!!

위 방법은 각 구간별로 지니계수를 짜서
최적의 Split Criterion (분할기준)을 찾아야한다.
➡️ Scikit Learn 으로 해결





2. Scikit Learn

  • import
from sklearn.tree import DecisionTreeClassifier

iris_tree = DecisionTreeClassifier()

  • data 확인

    • 데이터 행열 확인

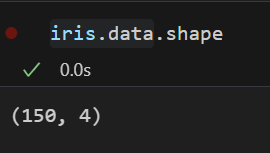
    • petal length & petal width의 데이터만 슬라이싱

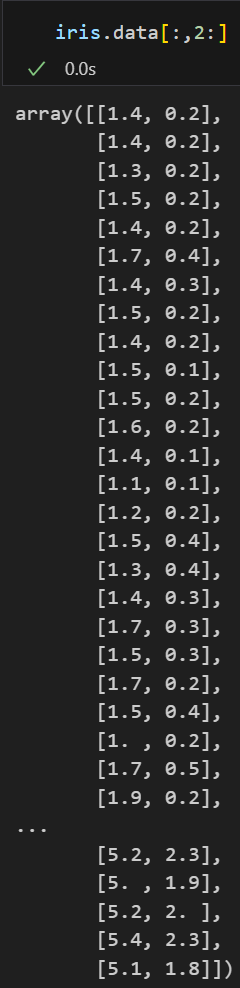
    • 어떤 종류인지 알 수 있는 데이터



(1) 학습 | fit

🧷 학습 시킬 모델명 : iris_tree

모델명.fit (데이터, 정답)

iris_tree.fit(iris.data[:,2:], iris.target)



(2) 예측 | predict

🧷 학습 된 모델명 : iris_tree

모델명.predict(예측할데이터)

y_pred_tr = iris_tree.predict(iris.data[:,2:])



(3) 확인 | accuracy_score()

  • import
from sklearn.metrics import accuracy_score

🧷 정답 : iris.target / 에측값 : y_pred_tr

accuracy_score(정답, 예측답)

from sklearn.metrics import accuracy_score
accuracy_score(iris.target, y_pred_tr)





3. 과적합

학습한 모델의 정확도가 학습 데이터 셋에 지나치게 적합하여,
새로운 데이터에 대한 성능이 감소할 수 있는데
이를 과적합 이라고 한다.


모델학습 확인 - (1) plot tree

from sklearn.tree import plot_tree

plt.figure(figsize=(12,8))
plot_tree(iris_tree)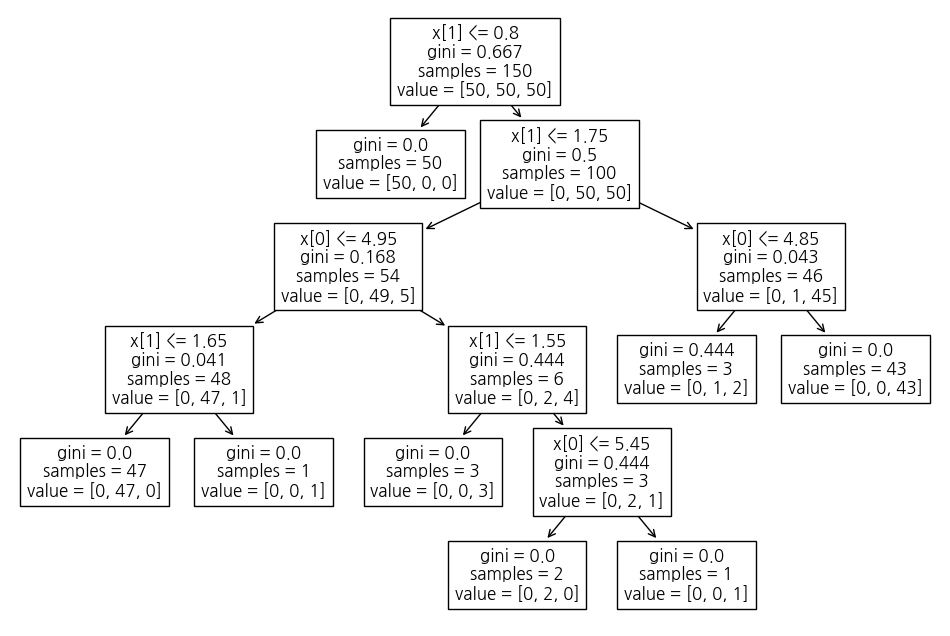

학습 데이터 셋의 경우의 수를 트리형태로 만든것


모델학습 확인 - (2) plot_decision_regions

  • 설치 : !pip install mlxtend
from mlxtend.plotting import plot_decision_regions

plt.Figure(figsize=(14,8))
plot_decision_regions(X=iris.data[:,2:], y=iris.target, clf=iris_tree, legend=2)
plt.show()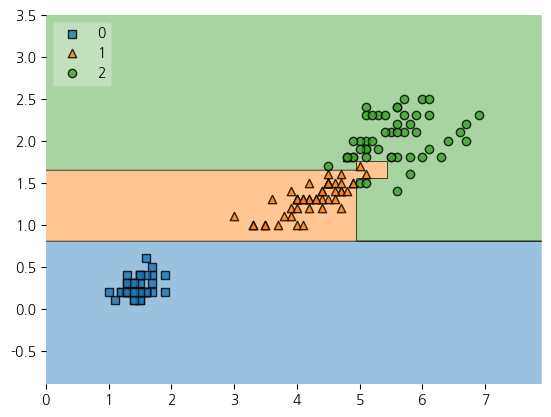

• 저 경계면은 올바른 걸까?
• 저 결과는 내가 가진 데이터를 벗어나서 일반화할 수 있는 걸까?
• 어차피 얻은(혹은 구한) 데이터는 유한하고 내가 얻은 데이터를 이용해서 일반화를 추구하게 된다.
• 이때 복잡한 경계면은 모델의 성능을 결국 나쁘게 만든다
➡️ 과적합

⬇️ 해결방법





4. 데이터분리


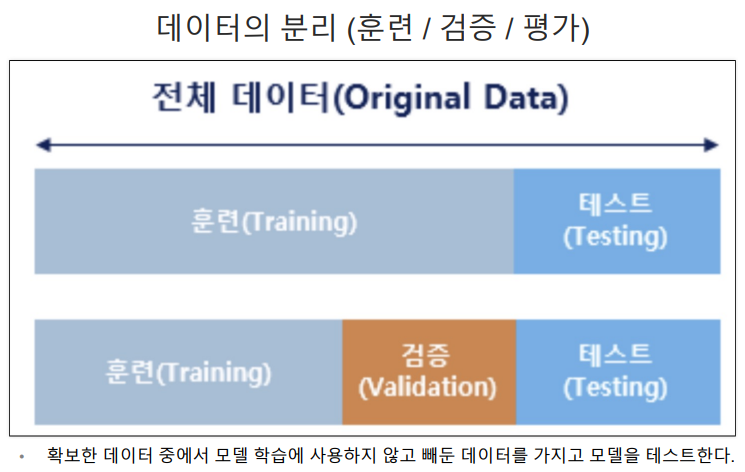
가지고 있는 데이터를 분리하여
한쪽은 학습을 진행하고, 나머지 데이터로 검증하는 방법



(1) 훈련 / 테스트 데이터 분리

from sklearn.model_selection import train_test_split

features = iris.data[:,2:]
labels = iris.target

X_train, X_test, y_train, y_test = train_test_split(features,labels, test_size=0.2, random_state=13) #test용 20%

  • X_train : 훈련시킬 80%의 petal length & petal width 데이터
  • X_test : 나머지 20%의 petal length & petal width 데이터
  • y_train : 훈련시킬 80%의 정답(품종no)
  • y_test : 나머지 20%의 정답(품종no)

(2) 분리 확인

as-is

import numpy as np

np.unique(y_test,return_counts=True)

➡️ (array([0, 1, 2]), array([ 9, 8, 13], dtype=int64))

여기서 각 0,1,2의 타겟 갯수가 달라서 맞춰줄예정

수정
(1)단계에서 stratify=labels 추가

# 각 타겟의 개수가 달라서 맞춰주는게 좋다
X_train, X_test, y_train, y_test = train_test_split(features,labels, 
                                                    test_size=0.2, 
                                                    stratify=labels,
                                                    random_state=13) #test용 20%

to-be

np.unique(y_test,return_counts=True)

➡️(array([0, 1, 2]), array([10, 10, 10], dtype=int64))


(3) 학습

from sklearn.tree import DecisionTreeClassifier

# max_depth : 성능제한 / 학습데이터셋에 과적합되지않게 하기위해
iris_tree = DecisionTreeClassifier(max_depth=2, random_state=13)
iris_tree.fit(X_train, y_train)

과적합을 막기위해 depth를 2로 제한


(4) tree & accuracy & plot_decision_regions 확인

  • tree
from sklearn.tree import plot_tree
import matplotlib.pyplot  as plt

plt.figure(figsize=(12,8))
plot_tree(iris_tree);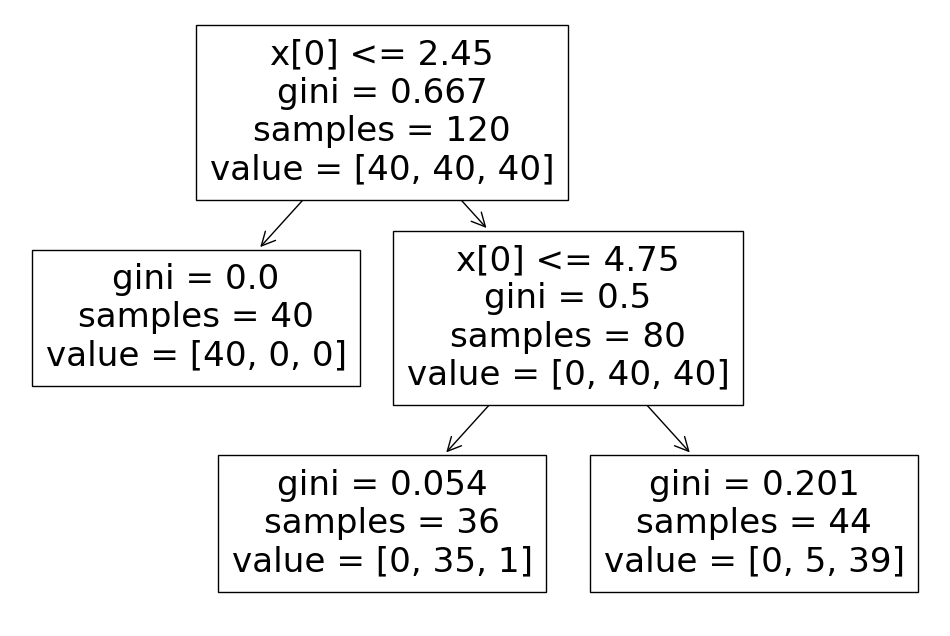

  • accuracy
y_pred_tr = iris_tree.predict(iris.data[:,2:])
y_pred_tr

from sklearn.metrics import accuracy_score
accuracy_score(iris.target, y_pred_tr)

➡️ 0.9533333333333334

  • plot_decision_regions
from mlxtend.plotting import plot_decision_regions

plt.Figure(figsize=(14,8))
plot_decision_regions(X=X_train, y=y_train, clf=iris_tree, legend=2)
plt.show()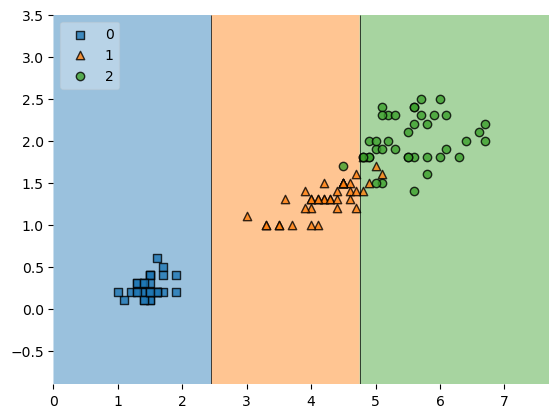


(5) 테스트데이터 확인

  • accuracy
y_pred_test = iris_tree.predict(X_test)
accuracy_score(y_test, y_pred_test)

➡️ 0.9666666666666667

  • plot_decision_regions
plt.Figure(figsize=(14,8))
plot_decision_regions(X=X_test, y=y_test, clf=iris_tree, legend=2)
plt.show()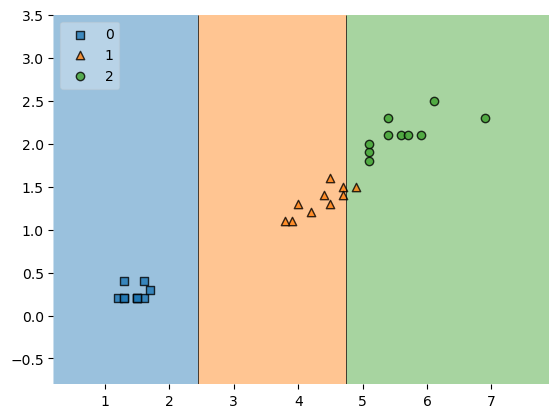


(6) 추가 - 전체데이터에 테스트데이터 표기하기

# 전체데이터 확인하기 (학습데이터+테스트데이터)
scatter_highlight_kwargs = {'s':150, 'label':'Test data', 'alpha':0.9}
scatter_kwargs = {'s':120, 'edgecolor':None, 'alpha':0.7}

plt.figure(figsize=(12,8))
plot_decision_regions(X=features, y=labels,
                      X_highlight=X_test,
                      clf=iris_tree,
                      legend=2,
                      scatter_highlight_kwargs=scatter_highlight_kwargs,
                      scatter_kwargs=scatter_kwargs,
                      contourf_kwargs={'alpha':0.2})
plt.show()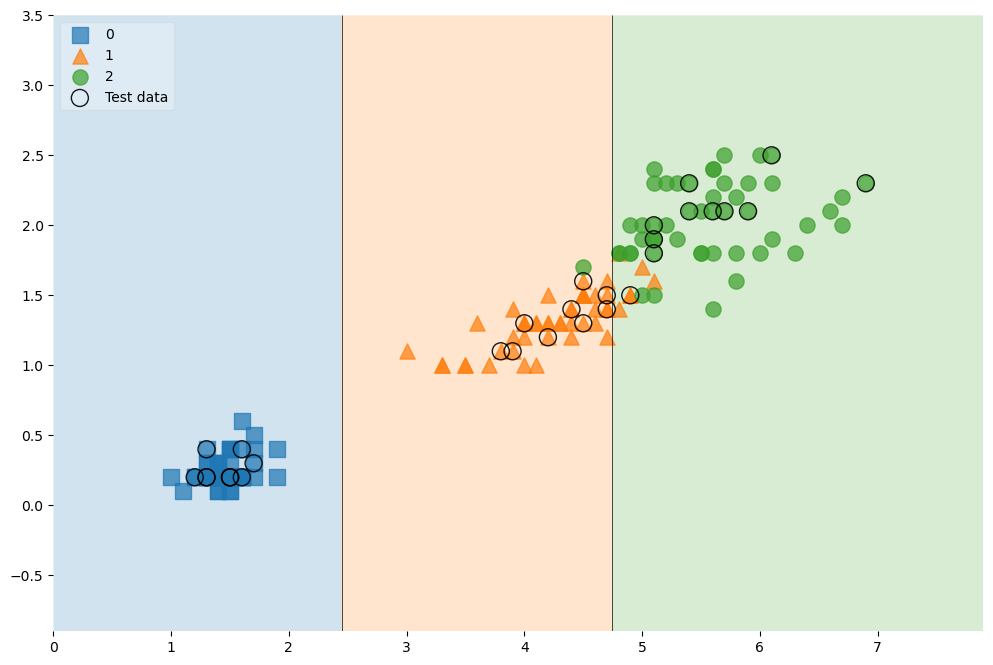





5. 학습모델 사용

(1) sepal과 petal 전체데이터로 학습

features = iris.data
labels = iris.target

# 데이터분리
X_train,X_test,y_train,y_test = train_test_split(features, labels,
                                                 test_size=0.2,
                                                 stratify=labels,
                                                 random_state=13)

#학습
iris_tree = DecisionTreeClassifier(max_depth=2, random_state=13)
iris_tree.fit(X_train,y_train)


(2) 모델사용

  • 길가다가 주운 iris가 sepal과 petal의 length, width가 각각 [4.3, 2. , 1.2, 1.0]이라면?

test_data = [[4.3, 2. , 1.2, 1.0]]
iris_tree.predict(test_data)
➡️ array([1])
: 1번품종

iris_tree.predict_proba(test_data)
➡️ array([[0. , 0.97222222, 0.02777778]])
: 각 품종별 확률

iris.target_names[iris_tree.predict(test_data)]
➡️ array(['versicolor'], dtype='<U10')
: 1번품종 이름


(3) 주요정보확인

iris_tree.feature_importances_
➡️ array([0. , 0. , 0.42189781, 0.57810219])

: 각 컬럼별 영향력

dict(zip(iris.feature_names,iris_tree.feature_importances_))
➡️ {'sepal length (cm)': 0.0,
'sepal width (cm)': 0.0,
'petal length (cm)': 0.421897810218978,
'petal width (cm)': 0.578102189781022}

단, depth가 2 (성능제한)인점 감안해야함


🧷 간단한 zip과 언패킹 알아보기
1. 리스트를 튜플로 zip

list1 = ['a','b','c']
list2 = [1,2,3]
pairs = [pair for pair in zip(list1, list2)]
pairs

➡️[('a', 1), ('b', 2), ('c', 3)]
2. 튜플을 dict으로
dict(pairs) ➡️ {'a': 1, 'b': 2, 'c': 3}
3. 한번에
dict(zip(list1, list2)) ➡️ {'a': 1, 'b': 2, 'c': 3}
4. 역변환

a,b = zip(*pairs)
list(a), list(b)

➡️ (['a', 'b', 'c'], [1, 2, 3])





Zero Base 데이터분석 스쿨
Daily Study Note
profile
솔비
Study Log
다음 포스트

ML - 2. 타이타닉 생존자 예측 w/ EDA

0개의 댓글

관련 채용 정보