💡그래프 알고리즘이란,
그래프와 같은 복잡하고 연결성이 높은 자료구조에서
순회 (Graph Traversal), 탐색 및 검색 (Graph Search) 등과 같은 목적으로 사용되는 알고리즘이다.
* 위상 정렬을 소개하기 전에 이해를 돕기 위해 필요한 알고리즘을 간단하게 소개하겠다.
그래프 순회 Graph Traversal
그래프 순회(Graph Traversal)는 그래프 내의 모든 정점을 중복 없이 방문하는 것을 목적으로 한다.
순회는 너비 우선 탐색 (Breadth-First Search, BFS)과 깊이 우선 탐색(Depth-Frist Search, DFS)로 나뉜다.
🏷️너비 우선 탐색 Breadth-First Search(BFS)
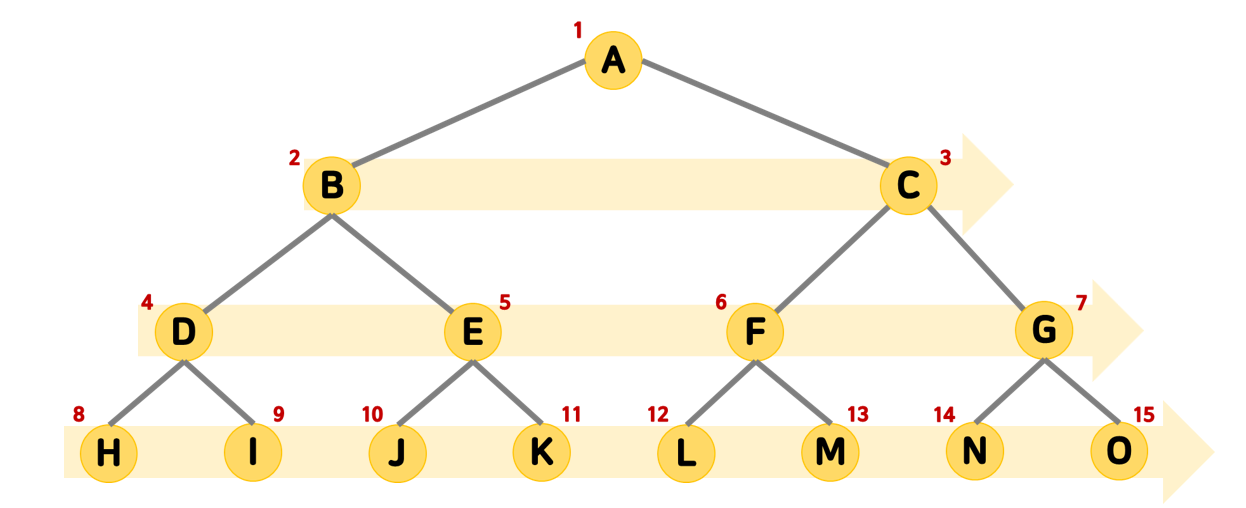
너비 우선 탐색은 특정 정점에서 시작해서 인접한 정점을 폭을 위주로 넓게(Wide) 탐색하는 방식이다.
🏷️깊이 우선 탐색 Depth-First Search(DFS)
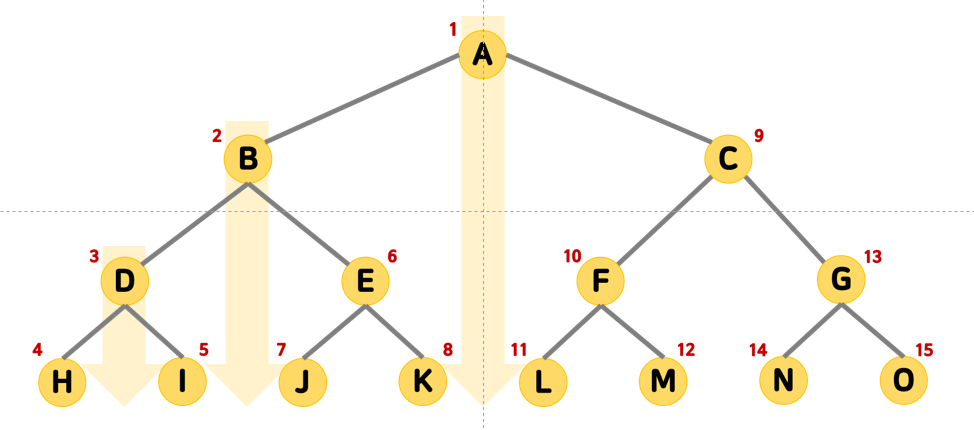
깊이 우선 탐색은 한 정점에서 인접한 정점으로 이동하기 전에 해당 정점의 모든 분기를 깊게(Deep) 탐색하는 방식이다.
깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 간단하게 구현할 수 있다.
위상 정렬 Topological Sort
💡알고리즘 원리💡
방향성이 있는 그래프에서 정점의 간선의 방향에 맞게 나열하는 방식의 정렬이다. 예를 들어, 순서에 맞게 작업을 수행해야 할 때 작업을 순서대로 정렬해주는 알고리즘이다.
🔗동작 과정 참고
위상 정렬은 진출 차수를 이용하는 DFS와 진입 차수를 이용하는 BFS 방식으로 구현할 수 있다.
진출 차수를 이용한 DFS
스택의 LIFO(Last-In First-Out) 구조를 활용하여 구현한다.
- 방문하지 않은 임의의 정점을 선택한다.
- 해당 정점에서 진출할 수 있는 정점을 스택에 저장한다.
- 모든 정점을 방문할 때까지 반복한다.
- 모든 정점을 방문했다면 위상 정렬 완료
▶ 스택에서 출력된 순서대로 정렬된다.
진입 차수를 이용한 BFS
큐의 FIFO(First-In First-Out) 구조를 활용하여 구현한다.
- 방문하지 않은 정점 중 진입 차수가 낮은 임의의 정점을 선택한다.
- 해당 정점은 제거한 후, 진출할 수 있는 정점의 진입 차수를 1만큼 감소시킨다.
- 진입 차수가 0이 된 정점을 큐에 저장한다.
- 큐가 비거나 모든 정점을 방문할 때까지 반복한다.
- 모든 정점을 방문했다면 위상 정렬 완료
▶ 제거된 순서대로 정렬된다.
🔎알고리즘 특징🔎
🔘 위상 정렬은 Directed Acyclic Graph (DAG) 에만 적용이 가능하다.
방향성이 있지만 순환성은 없는 DAG에만 적용이 가능하다. 방향성이 없다면 순서를 알 수 없고, 순환성이 있다면 시작 정점을 정할 수 없다.
🔘 위상 정렬은 유일한 답이 없다.
DFS/BFS 탐색 방식에 따라서 정렬 수행 결과가 달라지기 때문에 여러 가지 결과가 도출될 수 있다.
⏰시간 복잡도
시간 복잡도란,
문제를 해결하는데 걸리는 시간과 입력의 함수 관계를 나타내는 지표로,
주로 계수와 낮은 차수의 항을 제외시키는 빅-오 표기법을 사용한다.
V는 정점의 수, E는 간선의 수이다. 모든 정점을 확인하며 다른 정점과 연결된 간선을 확인해야 하기 때문에 의 시간복잡도를 보인다.
방식에 따른 시간복잡도에는 차이가 없다.
| 알고리즘 | DFS | BFS |
|---|---|---|
| 위상 정렬 |
💻코드 구현💻
진출 차수를 이용한 DFS
# 그래프 클래스
class Graph:
# 변수 정리
def __init__(self, v):
self.v = v #정점 수
self.edge = [[] for _ in range(v+1)] #간선 리스트
self.cycle = False #순환 기록
# 간선 추가
def add(self, i, o):
self.edge[i].append(o)
# DFS
def dfs(self, v):
self.visit[v] = 0 # 방문 표시
for n in self.edge[v]:
if self.visit[n]: # 방문하지 않았다면 DFS 수행
self.dfs(n)
elif self.finish[n]: # 방문했는데 더 이동할 수 있다면 순환 존재
self.cycle = True
return
# 더 이동할 수 없다면 종료하고 스택에 추가
self.finish[v] = 0
self.sort_list.append(v)
# 위상 정렬 수행
def topological_sort(self):
self.visit = [1]*(self.v+1) #방문 기록
self.finish = [1]*(self.v+1) #방문 기록
self.sort_list = [] #정렬 기록
for i in range(1, self.v):
if self.cycle: # 순환이 있다면 위상 정렬할 수 없음
return
if self.visit[i]:
self.dfs(i)
# 출력
while self.sort_list:
print(self.sort_list.pop(), end=' ')# 예제
g = Graph(5)
g.add(1,2)
g.add(1,3)
g.add(1,4)
g.add(2,5)
g.add(4,3)
print(g.edge) # 간선 리스트
g.topological_sort()
# [2, 3, 4], [5], [], [3], []
# 1 4 3 2 5 진입 차수를 이용한 BFS
from collections import deque
# 그래프 클래스
class Graph:
# 변수 정리
def __init__(self, v):
self.v = v #정점 수
self.indegree = [0] * (v+1)
self.edge = [[] for _ in range(v+1)] #간선 리스트
self.cycle = False #순환 기록
# 간선 추가
def add(self, i, o):
self.edge[i].append(o)
self.indegree[o] += 1 # 진입차수 증가
# 위상 정렬 수행
def topological_sort(self):
sort_list = []
q = deque() # 진입차수 0인 정점 기록
for i in range(1, self.v+1):
if not self.indegree[i]:
q.append(i)
while q: # 큐가 비었다면 순환 존재
v = q.popleft()
sort_list.append(v)
for n in self.edge[v]:
self.indegree[n] -= 1 # 진입차수 1 감소
if not self.indegree[n]: # 진입차수 0이면 큐에 저장
q.append(n)
# 출력
print(*sort_list)# 예제
g = Graph(5)
g.add(1,2)
g.add(1,3)
g.add(1,4)
g.add(2,5)
g.add(4,3)
print(g.edge)
g.topological_sort()
# [2, 3, 4], [5], [], [3], []
# 1 2 4 5 3