DP 개념을 간략하게 공부하고, 두번째로 마주한 문제이다.
처음에는 완전탐색을 생각했다. 모든 경우의수를 다 체크하는 것이다.
하지만, 완전탐색을 하게 된다면, 순서가 다를 경우, 다른 케이스로 취급된다.
예를 들면, 5원을 거슬러주는 경우, {1,2,3}, {1,3,2} 두 케이스를 동일 케이스로 봐야 하지만, 완전탐색을 하게 되면, 다른 케이스로 보게 된다.
내 힘으로 풀지 못하고, 풀이를 봤다.
핵심은, 6원에 대한 {1,2,5}의 경우의 수를 계산할 때, 6원에 대한 {1,2}의 경우의 수를 이용해야 한다는 것이다.
그렇다면 기존에 1,2원의 조합으로 만든 6원의 경우의수에 더해, 5원을 꼭 포함해서 6원을 만들 수 있는 경우의 수를 추가해 줘야한다.
5원을 꼭 포함해서 6원을 만들 수 있는 경우의 수는 어떻게 구할 수 있을까??
이걸 생각하는 부분이 가장 어려웠다..
결론적으로 6원에서 5원을 뺀 1원을 만들 수 있는 {1,2}원의 조합이 5를 꼭 포함해서 6을 만들 수 있는 조합이 된다.
왜냐하면, 1원을 만들 수 있는 조합{1}에 5를 추가하면 조합 {1,5}의 합은 6이 되기 때문이다.
그렇다면 dp[j - 1]k-money[j-1]]이 되야 하는 것이 아닐까?
그렇게 하면, 틀리게 된다.
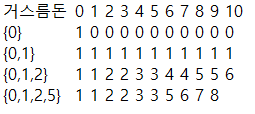
앞서 언급한 원리대로 {0,1}의 조합으로 3을 만드는 방법을 구한다면, {0}의 조합으로 3을 만드는 방법의 수 + {0}의 조합으로 2를 만드는 방법의 수가 된다.
그러면 0이 나오지만, 정답은 1이어야 한다.
1이 한번만 사용되는 경우만 고려되었고, 1이 중복으로 사용되는 경우가 고려되지 않았기 때문이다.
{0}의 조합으로 2를 만드는 방법의 수에는 1이 한번만 사용된 가정이 깔려있기 때문...
따라서 {0,1}의 조합으로 2를 만드는 방법의 수를 구해야 한다.
이 조합에 1을 추가하면,하나의 1을 추가해서 3을 만드는 {0,1}의 조합이 구해지기 때문이다.
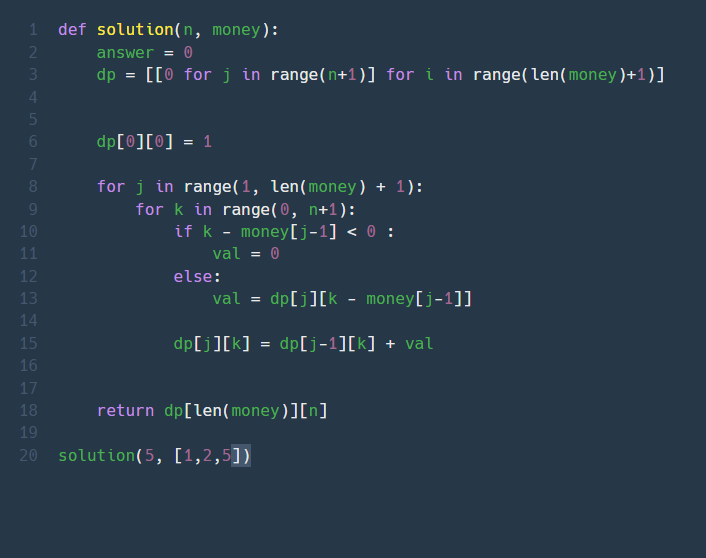
파이썬 코드는 아래와 같다.
이 문제는 솔직히 너무 어렵다
수학적으로 생각해야 할 부분이 많다.
두고두고 복기해야겠다.